10. 多段解法, 予測子修正子法
 Photo by Ghiffary Ridhwan on Unsplash
Photo by Ghiffary Ridhwan on Unsplash
常微分方程式の汎用解法: 線形多段解法や予測子修正子法を試してみよう
いろいろ慣れてきたところで、常微分方程式の汎用解法についてさらに学んでおこう. 「以前学んだ Runge-Kutta 法で十分じゃないか」という気持ちもあるかもしれないが、ここで学ぶ他の解法にはまた違った性質が有るのでいずれ役に立つだろう.
今回は題材として、カオス現象を引き起こす有名な方程式の一つである Lorenz 方程式を扱ってみる.
式としては従属変数 $u=u(t)$, $v=v(t)$, $w=w(t)$ に対する以下の様な連立常微分方程式が Lorenz 方程式である. ただし、$\sigma$, $r$, $b$ は定数パラメータである.
\[ \left\{ \begin{array}{rcl} \displaystyle \frac{d u}{dt} & = & \sigma (-u + v), \cr \displaystyle \frac{d v}{dt} & = & u (-w + r) - v, \cr \displaystyle \frac{d w}{dt} & = & u v - b w . \end{array} \right. \]
パラメータはいろいろ取りうるが、典型的なものはザルツマンのパラメータと言って次のような値だ. ここではこれを採用しよう.
$\sigma = 10$, $r = 28$, $b = 8 / 3$ .
線形多段解法, 予測子修正子法について
これから紹介するのは,Euler 法に似て高速 で Runge-Kutta法のように高精度 な解法である数値解法である. 良いこと尽くめな解法のように見えるが,「変化が激しい問題」にはあまり適していないのが欠点だ. ちなみに今回はうまくいくぞ.
線形多段解法(陽的アダムス法)
ここでは $du/dt = f(u,t)$ という一階の常微分方程式を想定しよう.
$t_n := n\Delta t$ と略記し、近似解や右辺の値なども $u_n \cong u(t_n)$, $f_n := f(u_n, t_n)$ と表記しよう.
そして、$t = t_n$ までは近似計算が進んでいて $u_{n+1}$ などを求める状況を考える. このとき、考えている常微分方程式の解に対して厳密に
\[ u(t_{n+1}) = u(t_n) + \int_{t_n}^{t_{n+1}} f(u(s), s) ds \]
が成り立つことから近似解を
\[ u_{n+1} = u_n + \int_{t_n}^{t_{n+1}} f(u(s), s) ds \]
とする、と考えるのは悪くない発想だ. よって、この右辺の積分を近似すれば、全体が近似できたことになる. このアイディアに基づいて議論をすすめてみよう.
積分の近似には、たとえば $t \in [t_n, t_{n+1}]$ における $f(u(t),t)$ を $t$ の多項式などでうまく近似する、という方法がある. 多項式の積分計算は簡単だしね.
そこで、どうにかして $f(u(t),t)$ を 多項式 $P(t)$ で近似することを考えよう.
計算過程の状況を考えると、すでに過去の近似計算過程によって、過去の値 $u_n, u_{n-1}, \cdots$ が求まっており、すなわち $f_n, f_{n-1}, \cdots$ も求まっている.
そこでこの既知の値 $f_n, f_{n-1}, \cdots$ を使って $t \in [t_n, t_{n+1}]$ における $f(u(t),t)$ の $t$ による近似多項式を求めることを考えよう.
もう少し詳しく言うと、関数 $f$ の $l$ 個の既知の離散値 $f_n, f_{n-1}, \cdots, f_{n-l+1}$ を用いて $t$ の $l-1$ 次多項式
\[ P_l(t) = C_0 + C_1 t + C_2 t^2 + \cdots + C_{l-1} t^{l-1} \]
で $f$ を近似しよう, そしてこれを積分しよう,というわけだ.
ちなみに、こういうケースのような任意の離散点での値を既知として得られる補間多項式を Legendre (補間)多項式 といい、その具体的かつ便利な計算方法はいくつか知られている.
ここではその計算方法のうち、この文脈で役に立つ Newton 補間多項式 (正確には Legendre 補間多項式の Newton 表示とでもいうべき)を使おう. 具体的には上の $P$ は次のようになる.
\[ \begin{array}{rcl} \!\!\!\!\!\!\!\!\!\!\!\! P_l(t) & = & \displaystyle f_n + \left( \frac{f_n - f_{n-1}}{\Delta t}\right) (t - t_n) + \left( \frac{f_n - 2f_{n-1} + f_{n-2}}{\Delta t^2}\right) \frac{ (t - t_n)(t - t_{n-1}) }{2} + \cr & & \displaystyle \cdots + \left( \frac{ \nabla^{l-1} f_n }{\Delta t^{l-1}} \right) \frac{ (t - t_n)(t - t_{n-1})\cdots(t - t_{n-l+1}) }{(l-1)!} . \end{array} \]
ここでは $\nabla$ は後退差分作用素で、作用される数列の添字を一つ増やす作用素を $s$ として(だから、$s^{-1}$ は添字を一つ減らす作用素だね),
$\nabla := ( 1 - s^{-1})$ と定義される.
まあ,
\[
\nabla f_n = f_n - f_{n-1}
\]
と思っておけばいい.
さて,この $P_l(t)$ の積分範囲が $[t_n, t_{n+1}]$ であることから $t = t_n + a \Delta t$, $\, 0< a <1$ と変数変換することにしてこの式を整理すると、
\[ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\! \hat{P_l}(a) = f_n + \nabla f_n \cdot a + \nabla^2 f_n \cdot a ( a+1 ) + \cdots + \nabla^{l-1} f_n \cdot a ( a+1 )( a+2 )\cdots(a+l-1) \]
となる. さらに(一般)二項係数
\[ \left( n \atop k \right) = \frac{n (n-1) \cdots (n-k+1)}{k!} \]
を利用すると1、より簡潔に
\[ \begin{array}{rcl} \hat{P_l}(a) & = & \displaystyle f_n - \nabla f_n \, \left( -a \atop 1 \right) + \nabla^2 f_n \, \left( -a \atop 2 \right) + \cdots + (-1)^{l-1} \nabla^{l-1} f_n \, \left( -a \atop l-1 \right) \cr & = & \displaystyle \sum_{k=0}^{l-1} (-1)^k \nabla^{k} f_n \, \left( -a \atop k \right) . \end{array} \]
と書ける.
さて、これで近似多項式 $P$ 相当が得られたことになるので、これを積分しよう.実際に変形すると
\[ \int_{t_n}^{t_{n+1}} P_l(t) dt = \Delta t \int_0^1 \hat{P_l}(a) da = \Delta t \sum_{k=0}^{l-1} \nabla^{k} f_n \, (-1)^k \int_0^1 \left( -a \atop k \right) da \label{eq:integrate-of-p} \]
となる.
そしてこの右辺の最後の部分にある積分 $(-1)^k \int_0^1 \left( -a \atop k \right) da$ は具体的に計算できる. これを定数扱いして、 \[ \gamma_k = (-1)^k \int_0^1 \left( -a \atop k \right) da \] とおこう. 実際には、 $\gamma_0 = 1$, $\gamma_1 = 1 / 2$, $\gamma_2 = 5 / 12$, $\gamma_3 = 3 / 8$, $\gamma_4 = 251 / 720$, $\cdots$ といった数字になる.
いい機会なので,この $\gamma_k$ を Julia で以下のように 数式処理で 計算して確認しよう.
まず,数式処理に使う SymPy package をインストールしよう(ちょっと時間がかかる).なお,既にインストールしてある人はもちろんこれをしなくてよい.
|
|
インストールが終わったら,次にこのパッケージの利用宣言と,数式処理で処理する変数(ここでは積分に使う独立変数 $x$ )の宣言を行う.
|
|
では $\gamma$ を求めるべく準備をしよう. 最初に一般化二項係数の定義をしよう.
|
|
ちなみに,これは数式処理で問題が起きにくいようにシンプルな定式化をしている.
次に $\gamma$ を定義する.ここで肝心なのが積分を数式処理で処理しているところで,プログラム内の integrate という関数がそれだ.
面倒な積分を手計算しなくて良いというのはありがたいね.
|
|
これで OK だ!
実際に,$k > 0$ でいくつか $\gamma_k$ を計算してみると次のように求まる.
|
|
1/2
|
|
5/12
|
|
3/8
|
|
251/720
よし.これで,$\gamma_k$ の値が数式処理で確認できたことになる.
このように,Julia を使えば数式処理もできる.数値計算と数式処理をうまく組み合わせればかなりのことができるので,なるべく使いこなそう.
さて,これで最終的に、$l$ 個の離散値 $f_n, f_{n-1}, \cdots, f_{n-l+1}$ を用いた近似計算式
\[ u_{n+1} = u_n + \Delta t \sum_{k=0}^{l-1} \gamma_k \nabla^{k} f_n . \]
が得られたことになる. こうした近似計算法は、結果として離散値 $f_n, f_{n-1}, \cdots, f_{n-l+1}$ を線形に足し合わせるだけなので、一般に $l$ 段の線形多段解法 と呼ばれる.
ちなみに,ここで導出したものは、既知の値(要するに過去の値)だけから計算できるので 陽的アダムス法 と呼ばれる.
陽的アダムス法の整理
上のようにして導出された陽的アダムス法を整理しておくと以下のようになる.
(1段. Euler 法と同じものになる) \[ u_{n+1} = u_n + \Delta t f_n . \]
(2段) \[ u_{n+1} = u_n + \Delta t \left( \frac{3}{2} f_n - \frac{1}{2} f_{n-1} \right) . \]
(3段) \[ u_{n+1} = u_n + \Delta t \left( \frac{23}{12} f_n - \frac{4}{3} f_{n-1} + \frac{5}{12} f_{n-2}\right) . \]
(4段) \[ u_{n+1} = u_n + \Delta t \left( \frac{35}{24} f_n - \frac{59}{24} f_{n-1} + \frac{37}{24} f_{n-2} - \frac{3}{8} f_{n-3} \right) . \]
web で検索するなどして、5段以上の陽的アダムス法を調べておこう.
陰的アダムス法
陽的アダムス法と異なり、新しい近似値による右辺の値 $f_{n+1}$ も多項式近似の参照値に使うのが陰的アダムス法である. 考え方はほぼ同じなのでいろいろ省略して結果だけ書くと、既知の離散値の個数を $l$ として,
\[ u_{n+1} = u_n + \Delta t \sum_{k=0}^l \tilde{\gamma_k} \nabla^{k} f_{n+1} \]
となる. ただし、
\[ \tilde{\gamma_k} := (-1)^k \int_0^1 \left( 1-a \atop k \right) da \]
で、これは $\tilde{\gamma_0} = 1$, $\tilde{\gamma_1} = -1 / 2$, $\tilde{\gamma_2} = -1 / 12$, $\tilde{\gamma_3} = -1 / 24$, $\tilde{\gamma_4} = -19 / 720$, $\cdots$ といった数字になる.
陰的アダムス法の整理
上のようにして導出された陰的アダムス法を整理しておくと以下のようになる. ただし、段数は「既知の離散値の個数 $l$」としてある.
(0段. 陰的 Euler 法と同じものになる) \[ u_{n+1} = u_n + \Delta t f_{n+1} . \]
(1段) \[ u_{n+1} = u_n + \Delta t \left( \frac{1}{2} f_{n+1} + \frac{1}{2} f_{n} \right) . \]
(2段) \[ u_{n+1} = u_n + \Delta t \left( \frac{5}{12} f_{n+1} + \frac{2}{3} f_{n} - \frac{1}{12} f_{n-1}\right) . \]
(3段) \[ u_{n+1} = u_n + \Delta t \left( \frac{3}{8} f_{n+1} + \frac{19}{24} f_{n} - \frac{5}{24} f_{n-1} + \frac{1}{24} f_{n-2}\right) . \]
これも web で検索するなどして、4段以上の陰的アダムス法を調べておこう.
予測子修正子法
予測子修正子法とは
- 「精度は悪いが速い」近似解法
- 「精度は良いが遅い」近似計算法
の2つの解法から「いいとこどりして,速くて精度の良い解法を作ろうとする」一般的な方法である.
一般的に書くとちょっと数式的にめんどくさいので、ここでは上の陽的アダムス法と陰的アダムス法を組み合わせた場合について例をあげて理解してもらおう.
まず、状況としては $u_n$, $f_n, f_{n-1}, \cdots, f_{n-l+1}$ が既知だとしよう. このとき、次のように各操作を定める.
| 操作 | 内容 |
|---|---|
| 操作 P (Predictor, 予測子) |
陽的アダムス法によって $u_n$, $f_n, f_{n-1}, \cdots, f_{n-l+1}$ から近似値 $u_{n+1}$ を求める. |
| 操作 E (Evaluator, 評価子) |
持っている新しい近似値 $u_{n+1}$ を用いて $f_{n+1} = f(u_{n+1}, t_{n+1})$ を計算する. |
| 操作 C (Corrector, 修正子) |
陰的アダムス法の「右辺」を 機械的に採用して $u_n$, $f_{n+1}, f_{n}, \cdots, f_{n-l+1}$ から近似値 $u_{n+1}$ を計算する. |
すると、例えば操作として P, E, C, E の順番に操作をすると、陰的計算「無し」で新しい近似値 $u_{n+1}$ を得られることになる. さらにこれに加えて C, E の操作を何度か繰り返すと、「収束して、本来の陰的アダムス法による近似値」$u_{n+1}$ に近い近似値が得られる可能性が高い.
操作 C は、本来の陰的アダムス法の「陰的性2」を無視してあたかも陽的解法のようであるかのように用いている.つまり、本来の陰的アダムス法ではなく、その粗い近似をしていることになる.
プログラミングへ
最終的に、予測子を 3段の陽的アダムス法 & 修正子を 3段の陰的アダムス法として,プログラミングをしてみよう.
まずは定数等の定義だ.
|
|
解きたい問題である Lorenz 方程式の右辺を定義してしまおう.r はパラメータの名前ですでに使っているので、関数 f とでもしておこうか.
|
|
線形多段解法では初期値が「余計にいくつか」必要だ. それらを求める方法はいろいろ考えられるが、まあ安直なのは Runge-Kutta 法かな. というわけで、Runge-Kutta 法による時間発展もプログラミングしてしまおう.
|
|
Runge-Kutta 法を使って、3段法に必要な離散値 $U_2,U_1,U_0, f_2, f_1, f_0$ を返す関数を作ろう
|
|
さて、まずは「真の」初期値を適当に用意しよう.
|
|
そして、これと上で用意した Runge-Kutta スキームを使って作られる後ろ 2ステップ分の初期値がどうなっているか, 試しに見てみよう.
|
|
3×3 Array{Float64,2}:
1.0 1.01257 1.04882
1.0 1.25992 1.524
1.0 0.984891 0.973114
|
|
3×3 Array{Float64,2}:
0.0 2.47351 4.75173
26.0 26.0947 26.8224
-1.66667 -1.35062 -0.996567
真の初期値 & 計算して作った2ステップ分の初期値の計3ステップ分の初期値の計算だが,まあ(数値はともかく)動いてはいるようだ.
では、線形多段解法 + 予測子修正子法のプログラムだ. 線形計算なので、線形代数の記号を使うと簡単にかけるはず だと考えて書こう.
|
|
早速、計算してみよう
|
|
試しに結果の数字をちょろっと見てみる.
|
|
3×3003 Array{Float64,2}:
1.0 1.01257 1.04882 1.07379 1.16296 … 2.87227 2.31572 1.8142
1.0 1.25992 1.524 1.78498 2.07339 -2.97887 -2.9685 -2.93744
1.0 0.984891 0.973114 0.959705 0.957358 29.1586 28.3153 27.5102
あまり変なことにはなっていなさそうなので、プロットしてみよう.
|
|
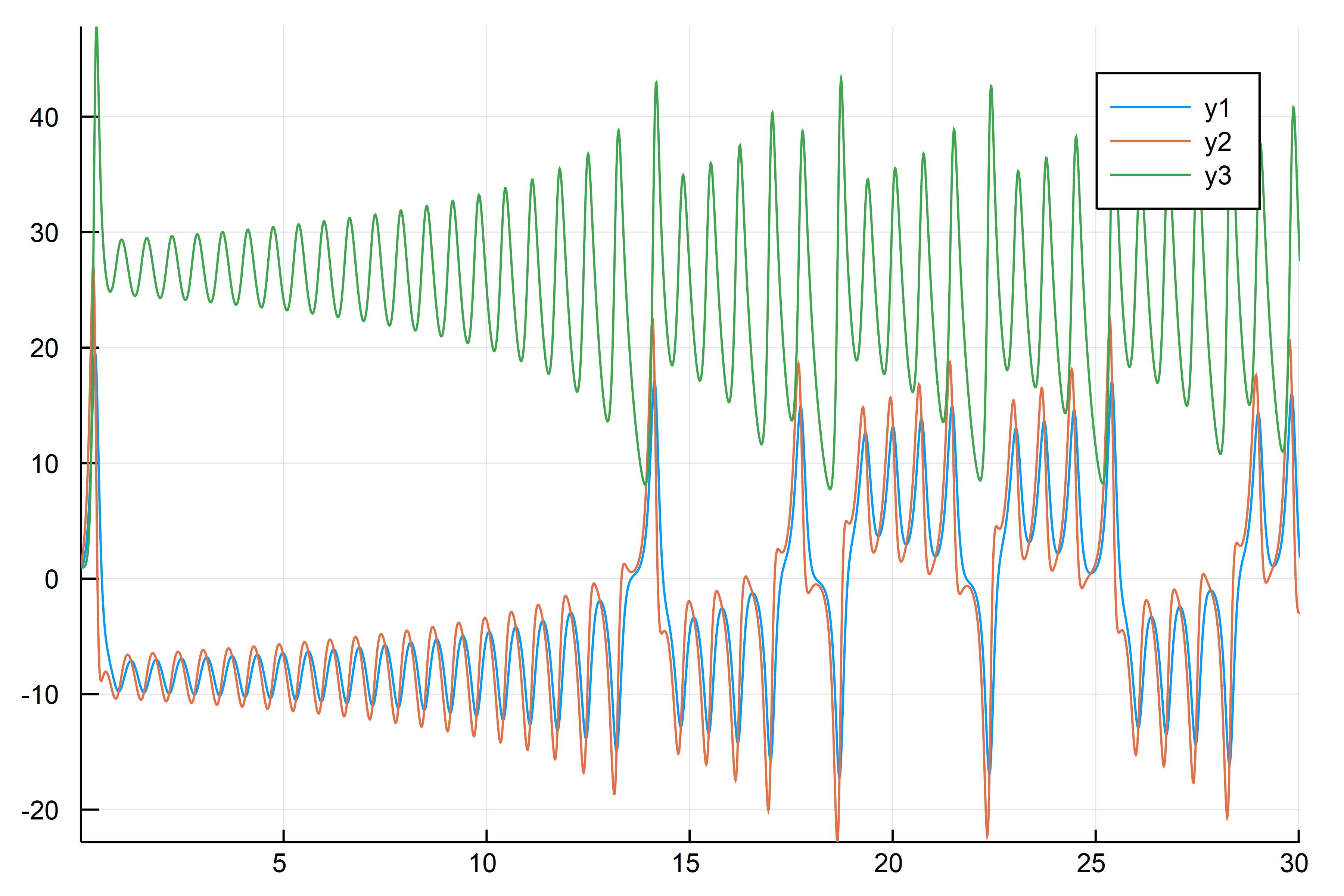
大丈夫そうだ.では、相図にして見てみよう.
|
|
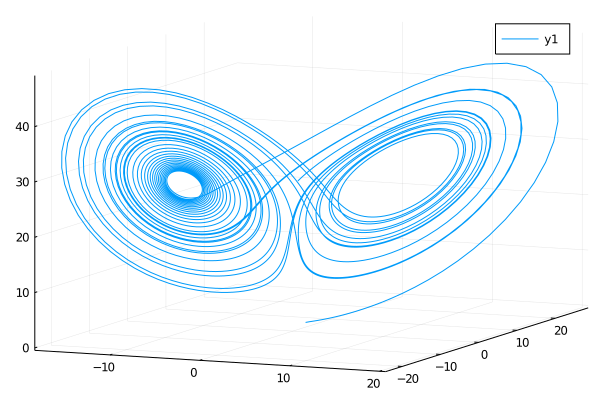
おお、大丈夫そうだな.それにしてもこの相図は興味深い.調べてみよう(→レポート課題へ)
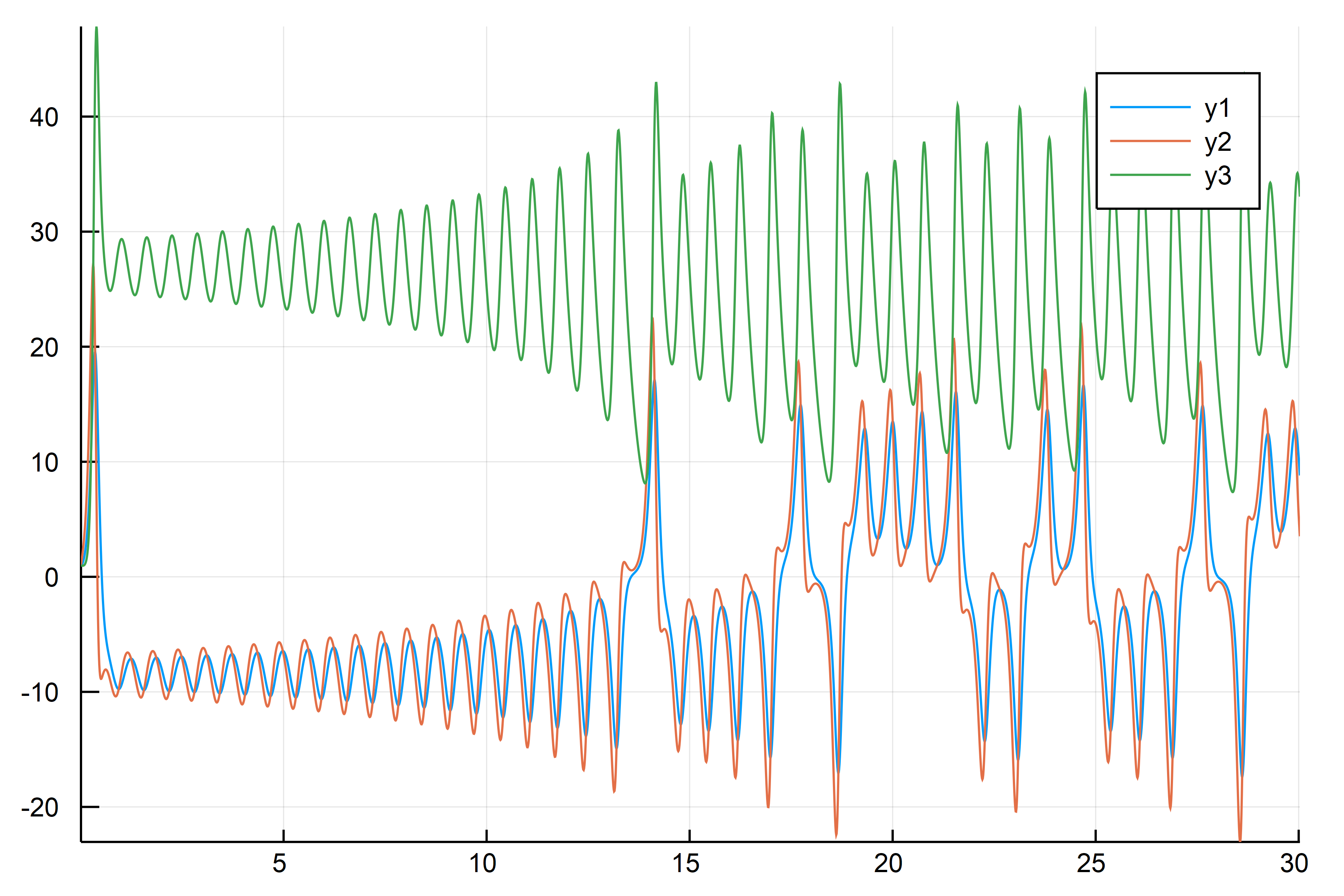
せっかくなので、全プロセスを Runge-Kutta 法で計算した場合でも似たような結果になることを確かめておこう.
|
|
|
|
|
|
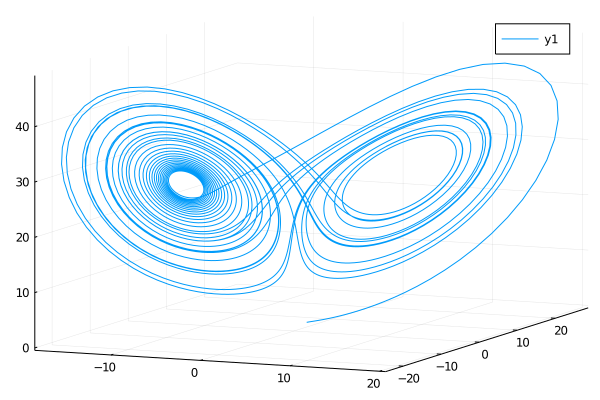
ふむ、どうやらどちらも計算結果は悪くはなさそうだ. しかし、結果は微妙に異なっていることにも留意しておこう.
速度比べだ!
線形多段解法は,Runge-Kutta法と比べても「いくらでも精度をあげられて,しかも,より速い」のがセールスポイントだ. ほんとかよ,ということでここで速度比較をしてみよう
よく考えると,線形多段解法は
- 精度はその段数による
- 段数とはすなわち過去のデータ数.計算時間にはほぼ関係しない.
- だから,計算時間はそのままで精度をどんどん上げられる
という,(理論的には)大変強力な特徴がある.そういう意味では(理論的には)最強な解法と言えよう.
さて話を戻して、初期値をいれたら最後の解を出力する形で両方の関数を作ろう.
まずは Runge-Kutta 法だ.
|
|
次に線形多段階法だ.
|
|
試しに一度両方動かしてみよう.値そのものはだいぶ違ってくることがわかる.
|
|
3-element Array{Float64,1}:
10.380754908974236
5.336383001817612
34.48595477125319
|
|
3-element Array{Float64,1}:
3.486917444133642
-2.9574191177496814
30.042166580039385
では、両方の速度を測ってみよう.
以前紹介した BenchmarkTools パッケージの @benchmark マクロを使おう.
まずは Runge-Kutta 法の速度を見よう.
|
|
BenchmarkTools.Trial:
memory estimate: 17.39 MiB
allocs estimate: 179983
--------------
minimum time: 6.298 ms (0.00% GC)
median time: 6.632 ms (0.00% GC)
mean time: 7.072 ms (7.03% GC)
maximum time: 12.208 ms (0.00% GC)
--------------
samples: 707
evals/sample: 1
次は線形多段解法の速度だ.
|
|
BenchmarkTools.Trial:
memory estimate: 15.41 MiB
allocs estimate: 140009
--------------
minimum time: 6.940 ms (0.00% GC)
median time: 7.223 ms (0.00% GC)
mean time: 7.872 ms (8.24% GC)
maximum time: 13.265 ms (13.61% GC)
--------------
samples: 635
evals/sample: 1
ふむ、理論的には微分値 $f(t,u)$ の評価回数が半分の線形多段解法が有利で、実際に計算時間もそうなっている…ようには見えんな. さて,なにがどうなっているのか?
プログラミング経験が多少ある人へ…
通常の言語によるプログラミング経験がある人だと、上の LM 関数は無駄が多くて遅いじゃん! 原因はそれだよ! と思うのではないだろうか. そしてたぶん確かにそうだと思うので,少し改善して確かめてみよう.
しかし、Julia ぐらいの近代言語になるとコンパイラが相当に優秀で最適化を頑張ってくれるので、普通に思うよりも無駄の影響は小さかったりするし、粗雑なプログラムに対して無駄を排除しようとするとプログラムが読みにくくなったり、エラーに弱くなったりする. なので、プログラムの最適化/高速化は、プログラムが動くようになり,プログラムがきれいになり,そしていろいろわかってきてからやろう. かの Knuth も次のような有名な言葉を残している.
早すぎる最適化は諸悪の根源である
"premature optimization is the root of all evil"
- Donald Knuth, Computer Programming as an Art, 1974, p.671.
ともあれ、無駄だと思わせる一部分を改善した次の関数 LM2 を使って, もとの LM より計算速度がどれくらい改善されるか見てみよう.
ちなみに、下で使っている @inbounds という命令は、配列の添字アクセスがはみ出てないかのエラーチェックを「しない」という命令だ.少しだけ計算が早くなるが、プログラムが完成してないうちは使わないほうがいいなあ…
|
|
まず、動くかどうか試そう.
|
|
3-element Array{Float64,1}:
3.486916208172385
-2.9574187195162067
30.042164383854004
ふむ、LM と同じ値になっているので,まあ無事に動くようだな.では、肝心の計算速度はどうかな?
|
|
BenchmarkTools.Trial:
memory estimate: 11.14 MiB
allocs estimate: 100021
--------------
minimum time: 4.256 ms (0.00% GC)
median time: 4.461 ms (0.00% GC)
mean time: 4.960 ms (9.81% GC)
maximum time: 9.866 ms (18.75% GC)
--------------
samples: 1008
evals/sample: 1
うん,速くなった. 確かに Runge-Kutta 法よりも速いね3. 必要なメモリ容量も少ないし,良いことばかりと言えよう.
あとは、関数 $f$ の計算が「大変になればなるほど」、この線形多段解法の計算の方が相対的に速くなるはずだ.
レポート
下記要領でレポートを出してみよう.
- e-mail にて,
- 題名を 2020-numerical-analysis-report-10 として,
- 教官宛(アドレスは web の "TOP" を見よう)に,
- 自分の学籍番号と名前を必ず書き込んで,
- 内容はテキストでも良いし,pdf などの電子ファイルを添付しても良いので,
下記の内容を実行して,結果や解析,感想等をレポートとして提出しよう.
- 上の説明の最初の方にある定数 $\gamma_k$, $\tilde{\gamma}_k$ について,
$\gamma_5$, $\gamma_6$, $\gamma_7$ および $\tilde{\gamma}_5$, $\tilde{\gamma}_6$, $\tilde{\gamma}_7$ を求めよ. - Lorenz 方程式の相図上での近似解の動きを動画にしてみよう
- なんらかの資料を探して、Lorenz 方程式の数学的な特徴を調べて報告せよ.とくに、数値計算の結果の良し悪しをチェックするのに役に立ちそうな特徴について詳しく調べよう.
-
ここでは $k=0$ のときの一般二項係数を $\left(n \atop 0\right) = 1$ としている. ↩︎
-
左辺に $u_{n+1}$ があって,右辺にも $f_{n+1}$ の中に $f_{n+1} = f(u_{n+1})$ という形で $u_{n+1}$ がある.だから本来はこの両辺が一致するような $u_{n+1}$ を探し求める問題(陰的問題)のはずなのだ,という意味. ↩︎
-
ただ,Runge-Kutta法に比べておおよそ 3/4 程度の計算時間なので,予想された 1/2 という計算時間よりはまだ遅めかな.問題がシンプルすぎて,関数値 $f$ の計算ではない他の計算部分(線形計算等)の計算時間が強く反映されてしまっているんだろうね. ↩︎
