ゼロ点を求める¹

そもそも論で言えば，コンピュータで計算する問題！というとたいそう難しく聞こえる．しかしまあ，おおざっぱには多くの問題は以下のふたつの問題を組み合わせたものだと考えられるだろうから，なんとかなりそうな気もするね？

制約を満たす解を求める問題: 例. $\sin(x) = 0.85$ を満たす $x$ を求める²．
(近似)解を式に代入してその妥当性を確認できるのが特徴．

なにかを最大・最小にする解を探す問題(最適化問題): 例. $x \in [-0.5,0.5]$ で $y = - x^2 - 5\exp(- 10^{5} \times x^2)$ (下記の図)の最小値を，$y$ の関数形を知らずに数値を比較することで探す. うまく見つかるだろうか？
運が良くなくて最小値を見逃す可能性があるよなあ．また，得た近似解が本当に最小値に近いかを調べる方法も難しい…

この授業の対象は基本的に前者だ．得た近似解がどれくらい妥当か，確認できる世界なのでそこは安心しよう．

そして今回はその中でも単純な，入力も出力も単なる実数である関数を考えて，その関数値がゼロになる入力値(ゼロ点)を求める，という問題, すなわち，一般的に \[ f(x) = 0 \,\, \mbox{ for } {}^{\exists} x \in \mathbb{R} \] な状況を想定してこの $x$ を求める問題を考えよう．

Newton 法を学ぶ

今回は，けっこう幅広いシーンで使える Newton 法というものを学ぼう．

これは「今持っている近似値より少しはマシな近似値を求める」=「改善する」ことを繰り返す方法³の一種なので，「どうやって近似解を改善するのか」がわかれば全体がわかることになるね(本当は，改善することを「期待する」だけなんだけどね)．

そしてその肝心の繰り返しの 1ステップ分の改善プロセスは，
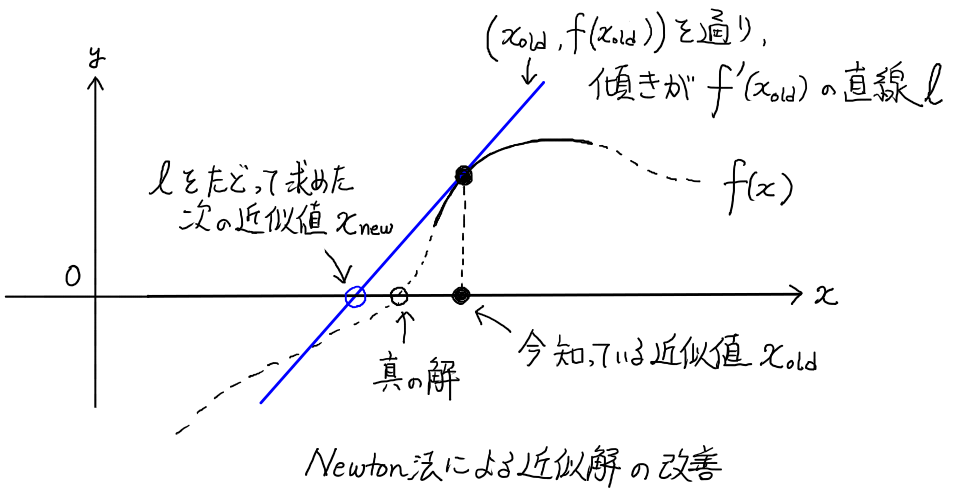
この図でおおよそわかるだろうが，図に合わせて説明するならば次のようになっている．

今もっている近似値 $x_{old}$ を用いて，関数値 $f(x_{old})$ とその微分値 $f'(x_{old})$ を「数値として」計算する．
$(x_{old}, f(x_{old}))$ を通って傾きが $f'(x_{old})$ な直線の式 \[ y - f(x_{old}) = f'(x_{old}) ( x - x_{old} ) \] を考える．
この直線が $x$軸と交わるところを「改善された次の近似値 $x_{new}$」だと定めよう⁴．
つまり，この直線の式に $y=0$ を代入して求まる $x$ がそれだということになるので， \[ x_{new} = x_{old} - f(x_{old}) / f'(x_{old}) \] として近似値が改善されることになる．これだけだ．

なお，この説明からわかるように，Newton 法は関数の「微分値」が計算できることが前提になっている．

例えば, $x^2 = 2$ を解いて解 $\sqrt{2}$ を求めてみよう．

さてやっと実際の話だ．ここからはこの Newton法を「実際に動かせるか」頑張ってみよう．

典型的な手法は、まずは問題を左辺 = 0 の形に直すところから始まる．

1

f(x) = x^2 - 2   # この関数 f のゼロ点が求めたい値だ．

さらに、Newton 法にはこの関数の微分形も必要だ．今回は幸い手で求まるので、与えてしまおう．

1

df(x) = 2x

さて実際に Newton 法を実行してみよう． Newton 法は近似解がだんだん良くなっていく(と期待する)反復解法なので、初期値を設定してから、ループを回すという形になる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


# 初期値．なるべく良い近似値がいいのだが, まあ適当に与えておこう．
x = 1.0

# グラフにしたいので、途中経過を配列に保存していく
sq = [ x ]  

# 反復改善する．うまくいかなくても 100回で停まる
for i in 1:100
    println("$i : $x, $(f(x))" ) # 状況を出力
    if abs(f(x)) < 1.0e-06     # f(x) が 0 に十分近ければ OK！
        break
    end
    x = x - f(x)/df(x)  # Newton 法による近似値更新！
    push!(sq, x)        # 新しい近似値を保存
end

1: 1.0, -1.0
2: 1.5, 0.25
3: 1.4166666666666667, 0.006944444444444642
4: 1.4142156862745099, 6.007304882871267e-6
5: 1.4142135623746899, 4.510614104447086e-12

どうやら Newton 法による改善が 4回行われ、5回目のループに入っての判定で終了となったようだ．この場合は、$x^2 - 2$ が大変小さくなっているようだ($10^{-12}$ぐらい)．

念のために、$\sqrt 2$ と x を比べてみよう．

1

√2, x

(1.4142135623730951, 1.4142135623746899)

大変近いな．実際の差も見ておこう．

1

√2 - x

-1.5947243525715749e-12

関数だけでなく、近似値の値そのものも 12桁ぐらいあっていることがわかる．この計算はうまくいったと言ってよいだろう．

誤差 abs$(\sqrt{2} - x)$ がどのように変化していくか、グラフにしてみよう．まずはいつもの準備をして…

1

using Plots

上で作った sq ベクトルを使って次のようにすればよいだろう．

1
2


error = abs.( sq .- √2 )
plot(error, marker = :auto)

誤差が急速に小さくなっていることが分かる．

上のプログラム中の，abs. や .- などの，オペレータに .(ドット) をつけた記述は，通常のスカラー計算を配列の各要素にそれぞれ作用させるという機能で，broadcast などと呼ばれる．気になる人はマニュアルの broadcasting という箇所を読んでみよう．

さらに、対数グラフにしてみようか．

1

plot(log10.(error), marker = :auto)

対数グラフで見ると、誤差が急速に小さくなっていることがよりはっきりと見て取れる．たいしたものだ．

欲張って、20桁の精度が出るかやってみよう

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


# 初期値．なるべく良い近似値がいいのだが, まあ適当に与えておこう．
x = 1.0

# グラフにしたいので、途中経過を配列に保存していく
sq = [ x ]  

# 反復改善する．うまくいかなくても 100回で停まる
for i in 1:100
    println("$i : $x, $(f(x))" ) # 状況を出力
    if abs(f(x)) < 1.0e-20     # 20桁あうか？
        break
    end
    x = x - f(x)/df(x)  # Newton 法による近似値更新！
    push!(sq, x)        # 新しい近似値を保存
end

1: 1.0, -1.0
2: 1.5, 0.25
3: 1.4166666666666667, 0.006944444444444642
4: 1.4142156862745099, 6.007304882871267e-6
5: 1.4142135623746899, 4.510614104447086e-12
6: 1.4142135623730951, 4.440892098500626e-16
7: 1.414213562373095, -4.440892098500626e-16
8: 1.4142135623730951, 4.440892098500626e-16
9: 1.414213562373095, -4.440892098500626e-16
10: 1.4142135623730951, 4.440892098500626e-16
…略…
95: 1.414213562373095, -4.440892098500626e-16
96: 1.4142135623730951, 4.440892098500626e-16
97: 1.414213562373095, -4.440892098500626e-16
98: 1.4142135623730951, 4.440892098500626e-16
99: 1.414213562373095, -4.440892098500626e-16
100: 1.4142135623730951, 4.440892098500626e-16

どうやら実質的に無限ループに陥ってしまったようだ．

これは、特に指定しなければ Julia では浮動小数点に有効桁数が約 16桁のシステム(float64, 倍精度とも言うね)が使われるからだ．この制限は Julia に限らず多くの環境で共通だ．これをなんとかするのには少し知識が必要なので、またいずれにしておこう．

ここで重要なのは、多くの計算機・プログラム環境ではそもそも約16桁以上の精度を求めようとするのはそのままでは無理ゲーだ、ということを知っておくことだ．何桁の精度が欲しいのか、常に意識しておくと健全だ．

発展: 多次元問題の場合は？

気になる人もいるだろうから，$n > 1$ で $f$ が $\mathbb{R}^n \rightarrow \mathbb{R}^n$ な写像のときの Newton 法も本質的には同じ考えだよ，ということをさらっと書いておこう．

ただし図示による説明は困難なので Taylor 展開で説明しよう．

前提は一緒で，最初に近似値 $\boldsymbol{x}_{old} \in \mathbb{R}^n$ を持っているとする．そして，次の(改善)近似値を $\boldsymbol{x}_{new} \in \mathbb{R}^n$ と書こう．

このとき，関数 $f(\boldsymbol{x}_{new})$ を，$\boldsymbol{x}_{old}$ を中心として 1次項まで Taylor 展開すると， \[ f(\boldsymbol{x}_{new}) \cong f(\boldsymbol{x}_{old}) + \nabla f(\boldsymbol{x}_{old})\cdot( \boldsymbol{x}_{new} - \boldsymbol{x}_{old} ) \] となることは大学入ってすぐの 1年生の微積分学で学んだよね？
ちなみに $\nabla f(\boldsymbol{x}_{old})$ は $(i,j)$成分が $\partial f_i/\partial x_j$ であるヤコビ行列だね．

そして，$\boldsymbol{x}_{new}$ は「改善された」ゼロ点近似値であることを期待している．これは $f(\boldsymbol{x}_{new}) \cong \boldsymbol{0}$ だと期待していることであるので，上の式は \[ \boldsymbol{0} \cong f(\boldsymbol{x}_{old}) + \nabla f(\boldsymbol{x}_{old})\cdot( \boldsymbol{x}_{new} - \boldsymbol{x}_{old} ) \] ということになる．だからあとは上の式を単純に変形して，連立一次方程式 \[ \nabla f(\boldsymbol{x}_{old})\cdot ( \boldsymbol{x}_{new} - \boldsymbol{x}_{old} ) \cong - f(\boldsymbol{x}_{old}) \] を解いて $\boldsymbol{x}_{new} - \boldsymbol{x}_{old}$ を数値的に求めて，それに $\boldsymbol{x}_{old}$ を足せば $\boldsymbol{x}_{new}$ が求まるということになる．
数式で書くなら \[ \boldsymbol{x}_{new} \cong \boldsymbol{x}_{old} - \left( \nabla f(\boldsymbol{x}_{old}) \right)^{-1} f(\boldsymbol{x}_{old}) \] という感じだね.

ただし，この数式をみてプログラムを組むときに，行列 $\nabla f(\boldsymbol{x}_{old})$ の逆行列 $\left( \nabla f(\boldsymbol{x}_{old}) \right)^{-1}$ を計算してはいけない！

逆行列を直接求める計算量はとんでもなく大きいうえに誤差もたっぷりはいってくる⁵．良いことはないのだ．思い出そう．「連立一次方程式を解く」のに逆行列は必要ないことを．

あくまで「連立一次方程式を解く」計算でプログラムを組もう．

やってみる

実際に \[ \left\{ \begin{eqnarray*} x + 2y & = & -1, \cr x^2 + 2y^2 & = & 1 \end{eqnarray*} \right. \] の近似解を Newton 法で求めてみよう．初期値を決めないといけないが，まあ適当に $(1.0, -1.0)$ あたりで．

プログラムを書く前に，Julia で連立一次方程式を解く文法だけ簡単に説明しておこう．

Julia では連立一次方程式 $A\boldsymbol{x} = \boldsymbol{b}$ を解くには

1

x = A \ b

と書くだけで良い⁶,⁷．これでこの連立一次方程式が解かれて，$\boldsymbol{x}$ がその解になる．

さて，話をすすめよう．まずはゼロになってほしいベクトル値関数とその微分であるヤコビ行列の定義だ．以下のような感じだ．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


# ゼロになってほしい関数
function f(v)    # 関数を定義するたぶん最も正式な方法
    x, y = v     # ベクトル v を成分 x,y にわけている
    return [     # 出力は 2x1 の縦ベクトルで．
      x+2y+1     # 式中にスペースを入れるな！ 行列の別要素とされてしまう
      x^2+2y^2-1   
    ]
end

# f の微分であるヤコビ行列
function J(v)
    x, y = v
    return [    # 出力は 2x2 の行列で．
        1 2
        2x 4y
    ]
end

次に，ベクトルのノルム計算を楽にやりたいので，線形計算ライブラリ LinearAlgebra を読み込む．これは標準インストール済みのライブラリなので，インストールは不要だ．

1

using LinearAlgebra

あとは先の例と同様に Newton 法を適用するだけだ．細かい部分は異なるが，全体は同じなことがわかるだろう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


# 初期値．なるべく良い近似値がいいのだが, まあ適当に与えておこう．
x = [1.0, -1.0]

# グラフにしたいので、途中経過を(2次元)配列に保存していく
sq = x 

# 反復改善する．うまくいかなくても 100回で停まる
for i in 1:100
    println("$i : $x, $(norm(f(x)))" ) # 状況を出力
    if norm(f(x)) < 1.0e-06     # f(x)のノルムが 0に近ければ OK！
        break
    end
    x = x - J(x) \ f(x)  # Newton 法による近似値更新！
    sq = hcat(sq, x)      # 新しい近似値を横につなげる形で保存
end

1 : [1.0, -1.0], 2.0
2 : [0.5, -0.75], 0.375
3 : [0.35, -0.675], 0.03375000000000017
4 : [0.33353658536585357, -0.6667682926829268], 0.0004065660321237452
5 : [0.33333336430743143, -0.6666666821537157], 6.19481976826819e-8

結果を見ると，近似値の更新が 4回行われて，5回めループの最初で「終了」したことがわかる．

試しに，2次元平面上で近似値がどう動いたかも見てみよう．次のようにすると見ることが出来る．

1
2
3
4


using Plots

plot(sq[1,:], sq[2,:], 
     st = :path, marker =:auto, markersize = [4,5,6,7,8])

後の方の近似解の点をより大きく表示しているので，どこが初期値でどこが最後の点かすぐわかる．この場合は，ほぼ直線状に解に向かって近似解が移動していることがわかるだろう．

レポート

下記要領でレポートを出してみよう．

e-mail にて，
題名を 2020-numerical-analysis-report-03 として,
教官宛(アドレスは web の "TOP" を見よう)に，
自分の学籍番号と名前を必ず書き込んで，
内容はテキストでも良いし，pdf などの電子ファイルを添付しても良いので，

下記の内容を実行して，結果や解析，感想等をレポートとして提出しよう．

自分で Newton 法を用いて $\sin(x) = 3 / 4$ の近似解を求めてみよう
上の例を参考にすれば、ほとんど即座にできるはずだ．そこで、できれば、見ないでやってみることにチャレンジしてみよう．
次に、応用問題として \[ \left\{\begin{array}{rcl} x + 2y + z & = & -1, \cr x^2 + 2y^2 + z^2 & = & 10, \cr \sin(x+y+z) & = & 0.7 \end{array}\right. \] の近似解を Newton 法で求めてみよう．考え方は上の例と同じだ．
$[x,y,z]$ の初期値はそうだなあ，$[1.0, 0.0, 0.0]$ あたりでいいだろう．

正しくは，ゼロ点ではなくて零点(れいてん)と呼称すべきなんだろうだけど，聞きとりやすいゼロ点と呼んでおくよ． ↩︎
例えば $x = 1.01598\cdots$ が解の一つ． ↩︎
繰り返して近似解を改善していく手法を一般に「反復法」と呼ぶよ．逆に一回の計算でいきなり(良い)近似解を求めようとする手法を「直接法」と呼んだりするよ． ↩︎
本当に改善されるかは知らん！が，まあ，期待するというわけだな．もちろん，数学的な条件を整えれば改善することが証明できるが，現場ではそんなこと考えてないケースがほとんどだろうなあ． ↩︎
まあ，$2 \times 2$ 行列みたいに小さい行列なら問題ないけど，一般には駄目よ，というお話． ↩︎
日本語Windows では \ (バックスラッシュ)と $\yen$ (半角の円マーク)は同じ文字コードだ．どちらの形が表示されるかは単に設定による．なので入力時にどちらが表示されても同じものなのでびっくりしなくてよい． ↩︎
詳しい人向けに書くと，この表記で連立一次方程式を解くように命令すると，通常は LU分解が行われる． ↩︎

数値計算法基礎 (2020)

03. Newton法!

ゼロ点を求める¹

Newton 法を学ぶ

例えば, $x^2 = 2$ を解いて解 $\sqrt{2}$ を求めてみよう．

欲張って、20桁の精度が出るかやってみよう

発展: 多次元問題の場合は？

やってみる

レポート

ゼロ点を求める1

Newton 法を学ぶ

例えば, $x^2 = 2$ を解いて解 $\sqrt{2}$ を求めてみよう．

欲張って、20桁の精度が出るかやってみよう

発展: 多次元問題の場合は？

やってみる

レポート

ゼロ点を求める¹