Photo by Pablo García Saldaña on Unsplash

前回はゼロ点を求めるのに「かなり使える」Newton 法について学んだ．今回は他の解法を学びつつ，「自分でなんとかするにはどう考えればよいか」という，アルゴリズムの萌芽について少し考えていこう．

二分法: 実質的に 1次元的な手法で，お気楽

ゼロ点を求める解法として，微分も不要というお気楽な二分法というものがある．これは実質的に関数が $f: \mathbb{R}^1 \rightarrow \mathbb{R}^1$ で連続でないと使えないが、なにしろわかり易いので「近似解を求める方法を作る」考え方を学ぶのには最適な方法の一つだろう．

この二分法も Newton法と同じく近似を少しずつ良くしていく反復解法で，連続な関数 $f: \mathbb{R}^1 \rightarrow \mathbb{R}^1$ に対して適用できる．ただ，Newton法と以下の点が異なる．

ゼロ点の近似解そのものを追うのではなく，「ゼロ点を確実に含んでいる区間」を(小さくすることで)追いかける
「その区間にゼロ点が確実に含まれていること」は，区間の左端 $x_l$ と右端 $x_r$ に対して \[ f(x_l) \cdot f(x_r) < 0 \label{a} \] であることで保証する．
区間の中点で区間を二分して出来た2つの区間のどちらかを新しい区間として採用することで「改善」とする
※ このとき，2つの区間のうち，式 $(\ref{a})$ が成り立つ区間を採用する．

この改善プロセスは，
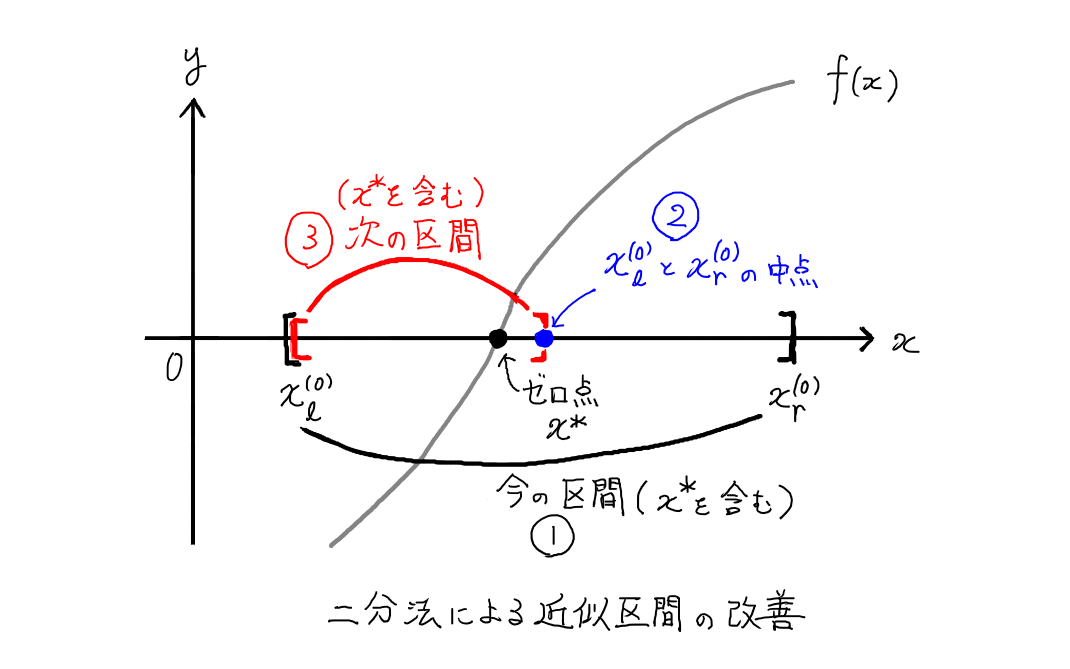
この図でもおおよそわかるだろう．もう少し数式を使って説明すると，次のようになっている．

まず、上記条件下で、 $f(x_{l})$ と $f(x_{r})$ が異符号であることが確認できるような区間 $\Omega = [x_{l}, x_{r}]$ をなんとか求めることができていると 仮定しよう (初期仮定)．

よって，$f(x)$ が連続である(前提)ことから、$\Omega$ の中に少なくとも１つは $f(x) = 0$ を満たす $x$ が存在する．

あとは簡単で、

区間の真ん中の値 $x_{av} = (x_{l} + x_{r})/2$ に対して $f(x_{av})$ の符号を調べる．
その符号と $f(x_{l})$, $f(x_{r})$ の符号を比較してその結果によって区間を更新する．

具体的には、$f(x_{l})$ の符号と $f(x_{av})$ の符号が異なるならば区間を $[x_{l}, x_{av}]$ に更新する．逆に $f(x_{av})$ の符号と $f(x_{l})$ の符号が同じならば区間を $[x_{av}, x_{r}] $ に更新する．

とすれば，区間が更新されるたびに大きさが半分になり，十分に繰り返せば区間が十分小さくなって、しかもその中に解があるはずなのでいつかは満足するよね… というのが二分法だ．

さて、二分法を試してみよう．例題として、

\[ \exp(x) = 2 \]

を満たす $x$ (要は $\log 2$ になるはず)を求めてみよう．

まず、$f(x) = 0$ の形に問題を書き直して、

1

f(x) = exp(x) - 2.0

次に，初期仮定を満たす $x_{left}, x_{right}$ を用意する．

この場合は、 $\exp(0) = 1 < 2 < \exp(1) = 2.71828...$ であることがすぐわかる．これはすなわち， \[ f(0) < 0 < f(1) \] ということで，関数 $f$ の値が $x=0$ と $x=1$ で異符号であることになる．

よって最初の区間としては $[0,1]$ を採用することにして，

1

left, right = 0.0, 1.0

とすれば良いだろう．

一応、 $f(x_{left})$ と $f(x_{right})$ の符号が異なることを確認しておこう.

1

f(left)*f(right)

-0.7182818284590451

うん、大丈夫だね．

では早速、二分法でこの区間( 初期は $[0,1]$ということになる )を半分ずつの大きさに小さくしていこう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


sq = [ left right ] # 最初はこの区間で、

for i in 0:100
    av = (left + right)/2 # 区間の真ん中の値

    println("$i : $left, $right : $(f(av))") # 状況を画面に

    if abs(f(av)) < 1.0e-8  # 8桁ぐらい合っていたらループを脱出
        break
    end

    if f(av)*f(left) < 0 # f(left)と f(av) が異なる符号ならば、という意味
        right = av # その場合は、次の区間は [ x_left, x_av ] にすればよい
    else
        left = av # 逆はこちら
    end
    sq = vcat(sq, [ left right ]) # 新しい区間を記録変数の「下」につけ加える
end

0: 0.0, 1.0: -0.3512787292998718
1: 0.5, 1.0: 0.11700001661267478
2: 0.5, 0.75: -0.13175404256777767
3: 0.625, 0.75: -0.011262530417708083
4: 0.6875, 0.75: 0.05186677348797675
5: 0.6875, 0.71875: 0.020055527708696452
6: 0.6875, 0.703125: 0.004335330874331245
7: 0.6875, 0.6953125: -0.003478832038737778
8: 0.69140625, 0.6953125: 0.0004244339097745353
9: 0.69140625, 0.693359375: -0.0015281520101939616
10: 0.6923828125, 0.693359375: -0.0005520974029782355
11: 0.69287109375, 0.693359375: -6.389134934270402e-5
12: 0.693115234375, 0.693359375: 0.00018025637771179603
13: 0.693115234375, 0.6932373046875: 5.8178788785667734e-5
14: 0.693115234375, 0.69317626953125: -2.8572115997604897e-6
15: 0.693145751953125, 0.69317626953125: 2.7660555759201344e-5
16: 0.693145751953125, 0.6931610107421875: 1.2401613871837469e-5
17: 0.693145751953125, 0.6931533813476562: 4.772186584123261e-6
18: 0.693145751953125, 0.6931495666503906: 9.574838539805341e-7
19: 0.693145751953125, 0.6931476593017578: -9.498647821626349e-7
20: 0.6931467056274414, 0.6931476593017578: 3.809308424251867e-9

ふむ、19回、区間を半分の大きさにして、良さげな感じの結果になっているようだ．

ためしに、区間がどうなったか、記録を見てみよう．

1

sq

21×2 Array{Float64,2}:
0.0       1.0
0.5       1.0
0.5       0.75
0.625     0.75
0.6875    0.75
0.6875    0.71875
0.6875    0.703125
0.6875    0.695313
0.691406  0.695313
0.691406  0.693359
0.692383  0.693359
0.692871  0.693359
0.693115  0.693359
0.693115  0.693237
0.693115  0.693176
0.693146  0.693176
0.693146  0.693161
0.693146  0.693153
0.693146  0.69315
0.693146  0.693148
0.693147  0.693148

そして、これをプロットしてみよう．次のような感じかな．まずいつものように

1

using Plots

としてから、

1
2
3


plot(sq, marker = :auto)

hline!( [ log(2.0) ]  )  # hline! は水平線を指定された高さで描く

とすれば良い．結果が下の図だ．

svg

このグラフで言えば$[y_1, y_2 ]$ が更新されていく区間ということになるが、それが毎回「半分の大きさ」になっていることに注意してグラフを見よう．

単純なだけに，二分法には「改良の余地」がありそうだ．考えてみよう(→ レポートの課題 3)．

入力が多次元の場合でも OK

考えている関数 $f$ が連続ならば，入力が多次元値でも二分法は使える．具体的には，$f: \mathbb{R}^n \rightarrow \mathbb{R}^1$, $n \geq 1$ のケースだね．

なぜ使えるのかは，
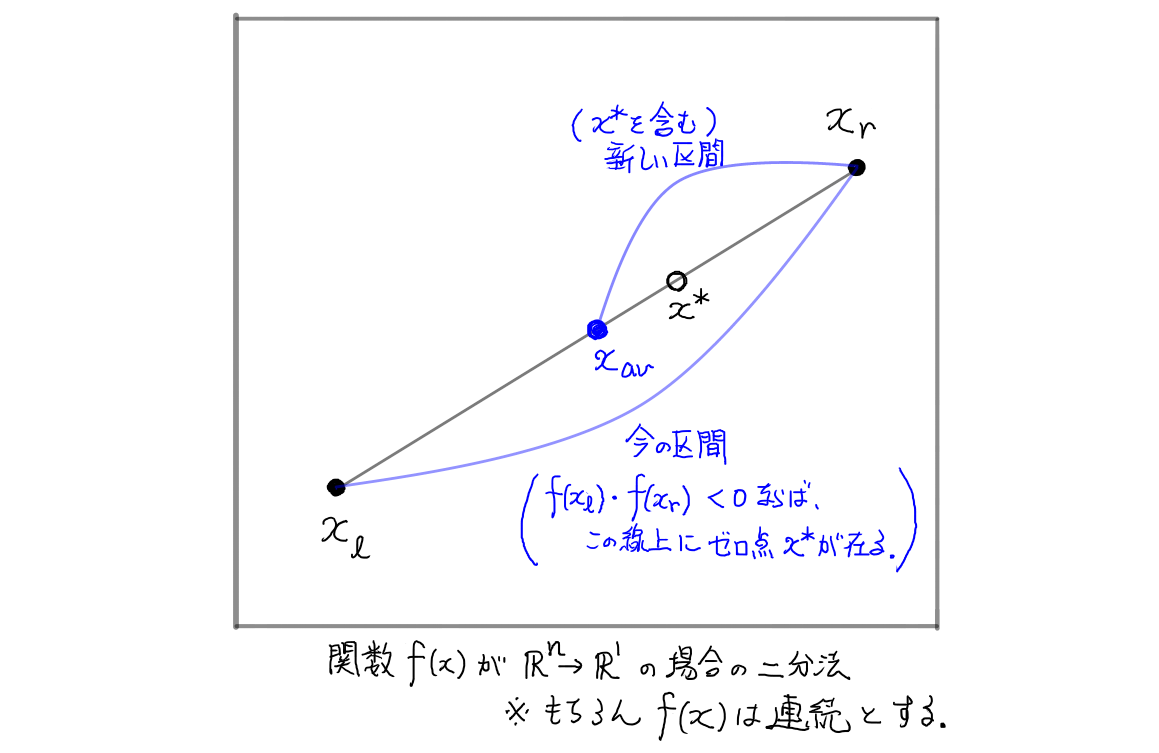
上の図をみれば一目瞭然だろう．

要するに，任意の 2点間の線分¹の上の関数 $f$ を考えると，関数 $f$ の連続性によりその線分の上でも関数は連続なので，単純に 1次元のときの問題と同じ状況になるのだ．

だから，「最初に関数 $f$ の値が異符号になるような 2点の $x$ を探すこと」 さえうまくいけばあとは単なる二分法そのものとなる．

ライブラリ NLsolve に頼ってみよう

自分で組んだ Newton 法や二分法等のルーチンがうまくうごかないような問題もあるだろう．それに、例えば Newton 法は微分関数を計算して求めておく必要があるし，二分法は1次元問題しか解けない．他の解法もそれぞれに欠点がある．

そこで、自作プログラムだけでなく，ケースバイケースで判断してくれる，ほぼ半自動の既存のライブラリを使えるようになっておこう．

今回は、NLsolve という、非線形方程式の近似根を求めるそのものズバリのライブラリ(Package)を使ってみよう．

パッケージの使い方

あらためて Julia のパッケージとはなにか、について話しておこう． julia には, 公開・配布されているライブラリがたくさんあり、これらがパッケージ(package)と呼ばれている．

Julia のパッケージリストは JuliaHub や Julia Observer で見られる．前者のほうがやや扱いやすいかな．

さて、こうしたパッケージの使い方はシンプルで、インストールして、あとは使うたびに呼び出すというだけだ．ここでは、NLsolve パッケージを例にして説明しよう．

インストール

NLsolve package は自分でインストールする必要がある(一回だけやれば良い)．その場合、julia 上で Pkg.add 命令を使ってインストールできる．この場合はパッケージ名 NLsolve を与えて

1
2


using Pkg
Pkg.add("NLsolve")

とすれば良い²．

パッケージの呼び出し

そのパッケージの機能を使う前にプログラム中で一度「使うよ」と宣言しておけば良い．先にやった Plots パッケージ等の場合と同じく、

using パッケージ名

とすれば良い．というわけで、(NLsolve のインストールが済んでいることを前提に)次のようにして使用宣言を今しておこう．

1

using NLsolve

NLsolve パッケージの使い方

このパッケージは非線形問題の汎用解法ライブラリなので、そのままだとちょっと使いにくい．詳しくは

NLsolve: 非線形方程式の求根 package

などを見てもらうとして、ここでは処方箋だけ書いておこう．

この処方箋とは、using NLsolve のあとに、続けて nls という関数を julia で定義しておいて、あとはこの関数 nls を使うという手である．このためには、この関数を定義しておかないといけないので、やっておこう．次のようになる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


function nls(func, params...; ini = [0.0])
    if typeof(ini) <: Number
        r = nlsolve((vout,vin)->vout[1]=func(vin[1],params...), [ini])
        v = r.zero[1]
    else
        r = nlsolve((vout,vin)->vout .= func(vin,params...), ini)
        v = r.zero
    end
    return v, r.f_converged
end

定義した関数 `nls` の使い方

スカラー問題と、ベクトル問題で分けて解説しておこう．

スカラー問題の場合

解きたい方程式が, スカラー変数 $x$ に対してスカラー値関数 $f$ を用いて $f(x,params)=0$ ($params$ はパラメータ, つまり、関数 $f$ の２つ目以降の引数) となっている場合は、

nls( f, params, ini = xの初期値 )

とすれば近似根を取り出せる．文法的に、初期値設定 ini = は省略できないが、params はあってもなくても複数でも良い．

ベクトル問題の場合

解きたい方程式が, ベクトル値変数 $\boldsymbol{x}$ に対してベクトル値関数 $\boldsymbol{f}$ を用いて $\boldsymbol{f}(\boldsymbol{x}, params) = \boldsymbol{0}$ (params はパラメータ、つまり、関数 $f$ の２つ目以降の引数) となっている場合は、

nls( f, params, ini = xの初期ベクトル )

とすれば近似根ベクトルを取り出せる．文法的に、初期値設定 ini = は省略できないが、params はあってもなくても複数でも良い．

スカラー問題をやってみる

パラメータがない、とても簡単な例をやってみよう． $\cos$ 関数の根、つまり、$\cos(x) = 1 / 7$ を満たす $x$ を一つ求めてみよう．それには、例えば近似根の初期値を $1.0$ などとして次のようにすれば良い．

1
2


f(x) = cos(x) - 1/7
res = nls(f, ini = 1.0)  # ini = 1.0 は近似根 x の探索初期値．

(1.4274487588352782, true)

すると上のように出力され、一つ目の数字が近似根で、２つめの "true" が「この近似根で $f \cong 0$ となっている」ことが確かめられる．

一応、近似根がうまく求まっていることを確認しておこう．

1
2


x = res[1]  # 並んでいるデータの一つ目を取り出す．
f(x)  # そして、f に代入して、ゼロに近いかどうかを見てみる．

-9.360467123631366e-10

結果は 0 に大変近い．確かに、この近似根は十分「良い」と言って良さそうだ．

ベクトルや集合 $v$ の第 $k$ 要素は、v[k] として表される．

次に、パラメータ(関数 $f$ の２つ目以降の引数のこと)が有る例をやってみよう．例として、パラメータ $p$ の平方根を求めるような問題を考えてみよう．それには､関数を $f(x,p) = x^2 - p$ としてこの根 $x$ を求めればいい．だから、次のようになるだろう．

1
2


f(x,p) = x^2 - p
nls(f, 2.0, ini=1.0) # 二つ目の引数 2.0 はパラメータ

(1.4142135623746899, true)

すると確かに $\sqrt{2}$ 相当が得られている．

パラメータは複数でも良いので、それを例でみてみよう．例えば、上の関数を少しだけいじって $f(x,p,q) = x^q - p$ としてこの根 $x$ を求める問題を考えよう．

1
2
3
4


f(x,p,q) = x^q - p

res = nls(f, 2.0, 2.1, ini=1.0) 
# x^(2.1) - 2.0 = 0 の近似根を求める

(1.391065619249075, true)

この値が確かに近似根になっていることは、結果の "true" 部分からも分かるが、確かめてみると、

1

res[1]^(2.1) - 2.0

9.798828415341632e-12

となるので、確認できる．

さて、近似根がうまく求まらない「はず」な問題も念のために扱ってみよう．単純なケースとして、負の数字の平方根を求めることに相当する近似根計算をさせてみよう．

1
2
3


f(x,p) = x^2 - p
nls(f, -0.0001, ini = 1.0)  
# x^2 = - 0.0001 を解こうとしているが、当然、実数解は存在しない…

(-4.385150007238086e-11, false)

出力をみると、(探索ルーチンが頑張って求めた)一見近似根っぽい数字が一つ目の出力項に出ているけれども、2つめの出力項の false によって、それは $f \cong 0$ を満足するような近似根ではない、という情報がわかる．つまり、

まともな近似解は求まらなかったよ！と言っている のである．

「ややこしい関数で近似根を求めさせると失敗するかも」というようなケースでは、この「計算に成功したかどうか」をきちんとチェックするようにプログラムを書いたほうが良さそうだ．

ベクトル値問題もやってみよう

入出力値がベクトルの問題もやってみよう．まずは前回(Newton法の回)で扱った連立非線形方程式問題に取り組んでみよう．

まず、対象となる関数を以前とまったく同じく定義して…

1
2
3
4
5
6
7


function f(vx)
    x, y = vx
    return [
        x+2y+1
        x^2+2y^2-1
    ]
end

で、適当な初期値をいれて関数 nls で解を求めてもらおう．

1

nls(f, ini = [1.0, 0.0])

([0.3333333341166318, -0.6666666670583159], true)

… いやあ、これは簡単だ． Newton 法のときは Jacobi行列を計算した上にプログラムしないといけなかったが、NLsolve を使っている限りそんな手間も不要だ．大変に楽だな．

次に、パラメータを持つ問題を扱ってみよう．例えばパラメータ $p,q$ に対して，

\[ \left\{\begin{array}{rcl} \cos^2(x) + \sin^2(y) & = & p, \cr \sin^2(x) - \cos^2(y) & = & q \end{array}\right. \]

という連立方程式を満たす近似根 $x,y$ が欲しいとしよう．

まず，この問題に対して等価な $h(\boldsymbol{x}, p, q) = \boldsymbol{0}$ という式を満たすように関数 $h$ を次のように定義しよう．

1
2
3
4


function h(u, p, q) 
    a,b = u
    return [ cos(a)^2 + sin(b)^2 - p, sin(a)^2 - cos(b)^2 - q ]
end 

試しに，適当な値を入れてこの関数が動作するかどうかチェックしてみる．

1

h([4.0,4.0], 0.5, 0.4)

2-element Array{Float64,1}:
0.5
-0.2544999661913866

確かに、ベクトル値が出力され、動作はきちんとしていそうだ．

では，上のご託宣に従って，近似根を求めてみよう．

1
2
3
4
5


p = 0.5
q = 0.4
ini_v = [4.0,4.0]

z = nls(h, p, q, ini = ini_v) # パラメータが複数でも大丈夫．

([4.486875574486246, 3.8769071064064615], true)

true と出ているので大丈夫なはずだが、この値が近似根になっていることを確認しておこう．

1

h(z[1], p, q)

2-element Array{Float64,1}:
 1.3633538742396922e-13
-1.3666845433135677e-13

確かにほぼゼロベクトルが出力されるので、OK と言って良さそうだ．

レポート

下記要領でレポートを出してみよう．

e-mail にて，
題名を 2020-numerical-analysis-report-04 として,
教官宛(アドレスは web の "TOP" を見よう)に，
自分の学籍番号と名前を必ず書き込んで，
内容はテキストでも良いし，pdf などの電子ファイルを添付しても良いので，

下記の内容を実行して，結果や解析，感想等をレポートとして提出しよう．

自分で $\sin(x) = 3 / 4$ の近似解を求めてみよう．具体的には，

二分法を用いて自分でプログラムして近似解を求める
NLsolve パッケージを使って近似解を求める

の両方をやろう．ほぼ即座にできるだろう．

非線形連立方程式の近似解も求めてみよう.
具体的には， \[ \left\{\begin{array}{rcl} x + 2y + z & = & -1, \cr x^2 + 2y^2 + z^2 & = & 10, \cr \sin(x+y+z) & = & 0.7 \end{array}\right. \] の近似解を,

NLsolve を使って
Newton 法で自力でプログラムして、

の両方で求めてみよう．

(チャレンジ課題) 自分で解法を考えよう
例えば $\sin(x) = 3 / 4$ の近似解を求める解法を「自分で創って」みよう．そして実際にプログラムをして動かして試してみよう．なお，まったく新しい解法でなく，Newton 法や二分法の改良でも良い．

まっすぐな線分でなくても良い．交差せずに滑らかに実区間 $[0,1]$ と 1対1 対応する曲線なら良い． ↩︎
REPL 環境(黒い文字だけの奴)でならば，"]" キーを押すと package 管理モードに入れて，add NLsolve と入力するだけで良い．そちらでも良いよ． ↩︎

数値計算法基礎 (2020)

04. ゼロ点求解法その他

二分法: 実質的に 1次元的な手法で，お気楽

入力が多次元の場合でも OK

ライブラリ NLsolve に頼ってみよう

パッケージの使い方

インストール

パッケージの呼び出し

NLsolve パッケージの使い方

定義した関数 `nls` の使い方

スカラー問題の場合

ベクトル問題の場合

スカラー問題をやってみる

ベクトル値問題もやってみよう

レポート

二分法: 実質的に 1次元的な手法で，お気楽

入力が多次元の場合でも OK

ライブラリ NLsolve に頼ってみよう

パッケージの使い方

インストール

パッケージの呼び出し

NLsolve パッケージの使い方

定義した関数 nls の使い方

スカラー問題の場合

ベクトル問題の場合

スカラー問題をやってみる

ベクトル値問題もやってみよう

レポート

定義した関数 `nls` の使い方