A2. 二階微分はどうよ: Newton運動方程式

Photo by Kamil Pietrzak on Unsplash

時間方向に二階微分が！

これまでは

\[ \frac{du}{dt} = F(u,t) \]

というタイプの、時間方向の微分が一階しかない時間発展問題の常微分方程式を扱ってきた．

しかしもちろんのことながら、われわれが取り組みたい問題はこういうものばかりではなく、例えば

\[ \frac{d^2 u}{dt^2} = F(u,\frac{du}{dt}, t) \]

といったような、時間方向の微分が二階の問題や、三階以上の問題も考えうる．

こういう場合にどうしたらよいか、それを学んでみよう．

いわゆる Newton 運動方程式

時間方向に二階微分が入る時間発展問題の常微分方程式といえば、高校時代に学ぶ Newton の運動方程式がまずは挙げられよう． そこで、ここではそれを扱ってみよう．

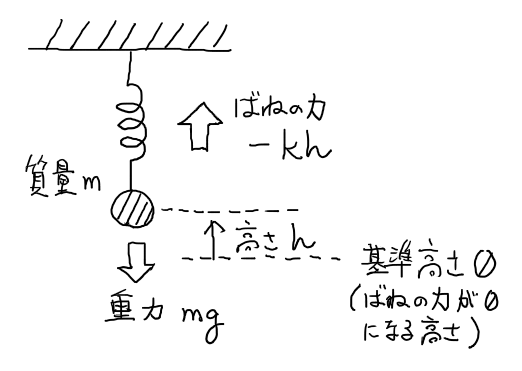
具体的には、バネでぶら下げられている重りの挙動を例として考えてみよう． バネ定数を $k$, 重りの重さを $m$, 重力定数を $g$ とすれば、重りの高さ位置 $h(t)$ $(t: $時間$)$ についての Newton の運動方程式は

\[ m \frac{d^2 h}{dt^2} = -kh -mg \]

となる． むろん、解をきちんと考えるためにはさらに初期値等の情報が必要で、例えば

\[ \left\{ \begin{array}{ccl} h(0) & = & h_{ini}, \cr \displaystyle \frac{dh}{dt}(0) & = & v_{ini} \end{array} \right. \]

などという情報を付与しないといけない．

さて、これを例に、しばらく考察を進めてみよう．

この問題は実は手計算で厳密解が求まる． 書いてしまうと， \[ \left\{ \begin{array}{ccl} h(t) & = & C \cos(\alpha t) + S \sin(\alpha t) + \beta , \cr \alpha & := & \sqrt{k/m}, \cr \beta & := & - mg/k \end{array} \right. \label{eq:strict-solution-form} \] という感じだ． ただし，定数 $C$, $S$ は初期条件で定まる量だね．

だから，上のように $h_{ini}$, $v_{ini}$ という初期条件を与える場合はさらに具体的に， \[ \left\{ \begin{array}{ccl} h(t) & = & C \cos(\alpha t) + S \sin(\alpha t) + \beta , \cr C & = & h_{ini} - \beta , \cr S & = & v_{ini}/\alpha , \cr \alpha & := & \sqrt{k/m} , \cr \beta & := & - mg/k , \cr \end{array} \right. \] と求まってしまう． まあ今回は「この厳密解を知らない体(ていと読む)で数値計算する」話になっているのでそのつもりで以下を読もう．

(計算その前に) 保存量

計算について考える前に、この系の保存量を考えてみよう． これは高校の物理で学んだ通りで、全エネルギー = 運動エネルギー ＋ 位置エネルギー が保存されるはずだ．

そして、運動エネルギーは

\[ \frac{1}{2} m \left( \frac{dh}{dt} \right)^2 \]

と表される．

位置エネルギーについては，位置エネルギー = "力の積分 on 逆らって移動した距離"" だったので

\[ \int_0^h (kx + mg) dx = \frac{1}{2} kh^2 + mgh \]

となることは覚えているだろうか？ まあそこは思い出してもらうとして、結論としてはこの計算によって全エネルギーは

\[ E(h(t)) = \frac{1}{2} m \left( \frac{dh}{dt} \right)^2 + \frac{1}{2} kh^2 + mgh \label{eq:energy-original} \]

となるわけなので、これがこの系の保存量である…はずだな．

高階微分問題への近似方法のアプローチ

さて，この問題をどう数値計算していくか，今から見ていこう． いくつかアプローチが考えられるので，先に分類を見せておこう．

それぞれ利点，欠点があるのでそのあたりに気をつけつつ，読んでいこう．

アプローチ 1: そのまま離散化

高階微分が含まれる時間発展問題へのアプローチはいくつか考えられるが、 いちばんストレートなのは

「方程式はそのままに、離散近似も素直に」

という手法だろう．

先のバネの問題に対しては，方程式はいじらずに，そして，離散化は 近似解を $h_n \cong h(n\Delta t)$, $n = 0,1, \cdots$ として

\[ \left\{ \begin{array}{ccl} \displaystyle m \left( \frac{h_{n+1} - 2h_n + h_{n-1} }{\Delta t^2} \right) & = & -k h_n - mg, \,\, n = 2, 3, \cdots , \cr \mbox{初期条件: }\, \, h_0 & \cong & h(0), \cr \mbox{初期条件: }\, \, h_1 & \cong & h(\Delta t) \end{array} \right. \]

という近似式を提案する、などだ． プログラムしやすいように少し変形すると次の式になる．

\[ \left\{ \begin{array}{ccl} h_{n+1} & = & \displaystyle \left( 2 - \frac{k\Delta t^2}{m} \right) h_n - h_{n-1} - g\Delta t^2 , \,\, n = 2, 3, \cdots , \cr \mbox{初期条件: }\, \, h_0 & \cong & h(0), \cr \mbox{初期条件: }\, \, h_1 & \cong & h(\Delta t) \end{array} \right. \]

この場合，初期条件の1つ目の具体化はあまり問題ないが，2つ目については $h(\Delta t)$ の値がわかっていないので困ってしまう． そこで，1ステップだけ他の方法で近似値を求めるなどのアイディアが必要になる． たとえば Euler 法的な近似を使うならば，まず下記のように考えて，

\[ \left\{ \begin{array}{ccl} h_0 & = & h_{ini} \, , \cr \mbox{Euler 法的に $v$ を近似: }\,\, v_{ini} & = & \displaystyle \frac{h_1 - h_0}{\Delta t} \end{array} \right. \]

これを整理した次の式を採用することになるだろう． これなら $h_{ini}$, $v_{ini}$ を使って $h_0$, $h_1$ が作れる．

\[ \left\{ \begin{array}{ccl} h_0 & = & h_{ini} \, , \cr h_1 & = & h_0 + v_{ini}\,\Delta t \end{array} \right. \]

これはあくまで「例」であって、良い離散化かどうかは全く考慮していない…

実際にやってみよう: アプローチ1

では早速，実際に動かしてみよう．

各種定数や初期値等をまず定義して…

1
2
3

m, k, g = 1.0, 1.0, 9.8 # 定数の設定
Δt = 0.1
h_ini, v_ini = 0.0, 1.0

上の初期値 h_ini, v_ini の値から， エネルギーの定義式 eq.$(\ref{eq:energy-original})$ を用いて すでに系のエネルギー値が計算できることに注意しておこう． この場合，エネルギー値は \[ E = 0.5 \] となる．確かめておこう．

さて話を戻して，次に， $h_n$ を h_curr , $h_{n-1}$ を h_old と書いて，新しい値 $h_{n+1}$ を返す関数を定義しよう．

1
2
3

function app_one(h_curr, h_old)
    return ( 2 - k*Δt^2/m ) * h_curr - h_old - g*Δt^2
end 

あとは初期条件の処理も合わせて，プログラムを全体を書いてしまおう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

# 初期条件2つ
h_old = h_ini
h_curr = h_old + v_ini * Δt

# データ記録
h_sq = [ h_old, h_curr ]

for i in 1:499 
    # 500 でも良いが，あとの例と合わせやすいのでこうしている

    h_new = app_one( h_curr, h_old )

    push!(h_sq, h_new) # データ記録
    h_curr, h_old = h_new, h_curr # 変数更新
end

近似解をプロットしよう．

手順はいつものとおり，

1

using Plots

としてから，わかりやすいように時間軸方向もデータを丁寧に用意して、

1

t_sq =  Δt * [ 0:500 ]

これまたいつものように次の命令で良い．

1

plot(t_sq, h_sq)

ふむ，悪くない数値解のように見える． 重りが振動している様子が出力されている様子だよね．

ここでこっそり，「知らない振りをしている厳密解」と比べてみよう．まずプログラムは次のような感じ．

1
2
3
4
5
6
7

function h_true(t)
    α = √(k/m)
    β = - m*g/k
    C = h_ini - β
    S = v_ini/α
    return C * cos(α*t) + S * sin(α*t) + β
end

数値解と厳密解を同時にプロットしてみよう．

1
2

plot( t_sq, h_sq ) # 数値解．こちらはデータプロット．
plot!( t_sq, h_true ) # 厳密解．こちらは関数プロット．

よほどひどい数値計算でない限り，まあ重なるよね． というわけで，「誤差」をプロットしよう．

1

plot(t_sq, h_sq .- h_true.( t_sq[1] )) # ちょっとテクニカルかな．

ふむ，近似解は結構あっているように見えたが，桁数で言えば 2桁ぐらいしか正しくないということのようだ．

上の例では，Julia の broadcast という機能を使っている．「ピリオド」がついている箇所がそうだね．
よくわからない人は，次のようにしても同じことができるのでそちらで理解しよう．

1
2

error_sq = [ h_sq[i+1] - h_true( i*Δt ) for i in 0:500 ]
plot( error_sq )

さて，この数値計算でエネルギーはどうなっただろうか． 確かめてみよう．

まず，エネルギーの計算式を作りたい…のだが， エネルギーの式 eq.$(\ref{eq:energy-original})$ を見るとわかるように，その定義には $dh/dt$ が含まれていて，$h(t)$ の近似値である $h_0, h_1, h_2, \cdots$ しか計算していない上の数値計算だと「どうやって $dh/dt$ の近似値を求めよう？」となってしまう．

まあしかたないので，「なるべく適切に近似」するように自分で決めるしかないね．

例えば，この数値計算法は(初期値の処理を除いて)時間方向に対称なので，エネルギーも時間方向に対称な近似をしたほうが適切だろうと考えて，一つの例として \[ \left( \left. \frac{dh}{dt} \right|_n \right)^2 \cong \displaystyle \frac{1}{2} \left\{ \left( \frac{h_{n+1} - h_n}{\Delta t} \right)^2 + \left( \frac{h_{n} - h_{n-1}}{\Delta t} \right)^2 \right\} \]

とし，次の式を使ってエネルギー値の近似とする方法があるね．ここではそうしておこう． \[ E_n = \displaystyle \frac{m}{4} \left\{ \left( \frac{h_{n+1} - h_n}{\Delta t} \right)^2 + \left( \frac{h_{n} - h_{n-1}}{\Delta t} \right)^2 \right\} + \frac{1}{2}kh_n^2 + mgh_n \]

これは $h_{n+1}$, $h_n$, $h_{n-1}$ の 3つの値から $t = n\Delta t$ でのエネルギー値 $E_n$ が求まるという形になっている. そこで，たとえばこれを h_new, h_curr, h_old の 3つの値をもらって E_n 相当を返す関数として作っておこう．

1
2
3
4
5
6
7
8
9

function E_n( h_new, h_curr, h_old )
    ke = (m/(4*Δt^2)) * ((h_new - h_curr)^2 + (h_curr - h_old)^2)
    # kinetic energy

    pe = (k/2) * h_curr^2 + m * g * h_curr
    # potential energy

    return  ke + pe
end

では，これを使ってエネルギー値を計算しながらもう一度計算しよう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

# 初期条件2つ
h_old = h_ini
h_curr = h_old + v_ini * Δt

# データ記録
h_sq = [ h_old, h_curr ]
E_sq = [ 0.0 ] # まだ計算できないのでダミーの数字を入れておく

for i in 1:499 
    # 500 でも良いが，あとの例と合わせやすいのでこうしている

    h_new = app_one( h_curr, h_old )

    push!(h_sq, h_new) # データ記録
    push!(E_sq, E_n(h_new, h_curr, h_old) ) # データ記録

    h_curr, h_old = h_new, h_curr # 変数更新
end

popfirst!(E_sq) # 最初のダミー数字を除去

さてエネルギーはどうかな？ まず数字を見てみよう(ちなみに，h_n よりもデータが 2つ少ないよね)．

1

E_sq

499-element Vector{Float64}:
 1.235025
 1.2350745025000003
 1.23024653235025
 1.2207337255597261
 1.206915643119367
 ⋮
 1.0859048467179022
 1.110261220668761
 1.13472017191485
 1.158305788301444
 1.1800770037347217

あれ？ 今の状況だと $E=0.5$ のはず．これはまずいな．

プロットでも確認しよう．

1

plot(E_sq)

値もおかしいし，上下に 10% ぐらいの振動もある． この様子だと，少なくともこのエネルギーの近似値はあまり信用できないなあ．

う～ん，状況をもう少し見るために，Δt の値を小さくして(誤差が小さくなると思われる)再計算して様子を見よう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

last_T = 50 
# 最終計算時間．さっきも t=50 ぐらいまで計算したので．

Δt = 0.001
# 2桁小さくしてみた．

N = Int(last_T/Δt)
# 計算回数

# 初期条件2つ
h_old = h_ini
h_curr = h_old + v_ini * Δt

# データ記録
h_sq = [ h_old, h_curr ]
E_sq = [ 0.0 ] # まだ計算できないのでダミーの数字を入れておく

for i in 1:N

    h_new = app_one( h_curr, h_old )

    push!(h_sq, h_new) # データ記録
    push!(E_sq, E_n(h_new, h_curr, h_old) ) # データ記録

    h_curr, h_old = h_new, h_curr # 変数更新
end

popfirst!(E_sq) # 最初のダミー数字を除去

まずは近似解 h_n の確認だ．

1

plot(h_sq)

さっきのグラフと比較しても，近似解は悪くなさそうだということがわかる．

一応誤差も見ておこう．

1
2

t_sq = Δt * [0:N+1]
plot(t_sq, h_sq .- h_true.( t_sq[1] ))

う～ん，誤差は 2桁小さくなっているな．Δt を2桁小さくしたら誤差も同じように2桁小さくなった，ということで，これは この計算法は精度でいえば一次精度, つまり \[ \mbox{error} \cong O(\Delta) \] ということかなあ． 計算法そのものは時間方向に対称なので二次精度 ($\mbox{error} \cong O(\Delta^2)$) なんだけど，初期値の作り方が Euler的で一次精度になってしまっているのが原因なんだろうな． あまり良くないねえ．

さて，ではエネルギーはどうだろうか． 近似エネルギー値 E_n 値をまずはみてみよう．

1

E_sq

50000-element Vector{Float64}:
 0.5049240149002502
 0.5049240197529657
 0.5049240245581272
 0.5049240293157156
 0.5049240340257121
 ⋮
 0.5049210620561304
 0.5049210784579437
 0.5049210948237981
 0.5049211111535099
 0.5049211274472656

おや？ 値がだいぶ $E = 0.5$ に近くなったな． 振動も小さくなったようだ． 初期値を引いた差をプロットしてみよう．

1

plot( E_sq .- E_sq[1] )

4桁ぐらい保たれるようになったな．まあなんとか及第点か．

全体としては，う～ん，そうだなあ，このアプローチは数値解そのものは近似は悪くなさそうだが，エネルギー値など「系の性質」をみるような量を計算してみると状況は良くないね． この場合は Δt をかなり小さくとらないとダメだねえ．

なので，このアプローチ 1 については以下のような感じだ．

• 数値計算の為の式は作りやすい．
• プログラムも簡単だ．
• 初期値の処理に困るかも…, エネルギー値の近似に困るかも… 等々，理論との整合性を保つのに困るシーンがありうる．
• 数値計算の結果は悪くないが，精度は低い．エネルギー値などはあまり良くない．エネルギー値を調べるなら Δt を相当小さくしないとダメ．

というわけで，このアプローチ 1 は「ひどく悪いわけではないが，オススメしにくいアプローチ」というところかな．

アプローチ 2: 式はそのままに，離散化に工夫を加える

アプローチ 1 の改善版として考えられるアプローチは、「方程式はそのままに、離散化は工夫して」という手法だろう． これは悪くないアプローチだが、説明が少し必要だ．いずれ時間に余裕があったならばそこで解説するとしよう．

アプローチ 3: 式を変形！ 離散化は素直に

次に考えられるアプローチは、「従属変数を新たに必要なだけ導入して方程式を一階常微分方程式に変形し、その常微分方程式に対する汎用解法を適用する」という手法だ． これはこうした問題の王道なので，以下の内容をよく理解しておこう．

話は簡単で、従属変数を新たに一つ導入すると全体の微分階数が 1階下げられるので(方程式は連立になる), これを必要なだけ繰り返せば良い． 具体的に上の例で示してみよう．

まず、従属変数として、

\[ v(t) := \frac{dh}{dt} \]

を新たに導入する．すると元の方程式そのものは

\[ m\frac{d v}{dt} = -kh -mg \]

と書き換えることができて微分階数を一つ下げられる． よって全体としては，連立ではあるが一階常微分方程式である次の形

\[ \left\{ \begin{array}{rcl} \displaystyle \frac{d h}{dt} & = & v, \cr \displaystyle m \frac{d v}{dt} & = & -kh -mg \end{array} \right. \]

に帰着できるというわけだ．

そして，この変形後の問題はこれまで見てきた一階微分方程式そのものであるので， Euler 法でも時間対称離散化でも Runge-Kutta 法でも，よく知られた汎用解法を適用できる という利点がある．これは大きいね．

この「変形後」の全エネルギーは，$h$ だけではなく $v$ も使った

\[ E(h,v) = \frac{1}{2} m v^2 + \frac{1}{2} kh^2 + mgh \]

と表現した方が良さそうだ．というのも，この式の中に微分が登場しないので扱いやすそうだからね．

実際にやってみよう: Euler 法

Euler 法だと、近似値を $h_n \cong h(n\Delta t)$, $v_n \cong v(n\Delta t)$ として, まあ普通は近似式は次のようになるかな．

\[ \left\{ \begin{array}{rcl} \displaystyle \frac{h_{n+1} - h_n}{\Delta t} & = & v_n, \cr \displaystyle m \left( \frac{v_{n+1} - v_n}{\Delta t} \right) & = & -k h_n -mg . \end{array} \right. \]

プログラムに向いた形に書き換えると次のような感じだ．

\[ \left\{ \begin{array}{rcl} h_{n+1} & = & h_n + \Delta t \, v_n, \cr v_{n+1} & = & \displaystyle v_n - \Delta t \, (\frac{k}{m} h_n + g), \end{array} \right. \]

あとはプログラミングだ．

Euler 法の 1step を関数としていつものように定義しよう．

1
2
3
4
5
6

function euler(h,v)
    h_new = h + Δt * v  
    v_new = v + Δt * (-(k/m)*h - g)

    return h_new, v_new
end

エネルギーの計算式も定義しておいて、

1

energy(h,v) = (m/2)*v^2 + (k/2)*h^2 + m*g*h

早速動かしてみようではないか！

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

Δt = 0.1 # さっき変えたので戻しておく．

h,v = h_ini, v_ini
h_sq = [h]
v_sq = [v]
E_sq = [ energy(h,v) ]

for i in 1:500
    h,v = euler(h,v)
    push!(h_sq, h)
    push!(v_sq, v)
    push!(E_sq, energy(h,v))
end

近似解をプロットしてみよう．

1

plot(h_sq)

う～ん、Euler法の欠点がもろに出ているね． 保存系なのに振幅が大きくなっている… 悪い意味で，厳密解と比較するまでもないな，こりゃ．

まあ「良くない」だろうけど念の為にエネルギーもプロットして確認しておこう．

1

plot(E_sq)

う～ん、エネルギーがすごい勢いで「増えている」．こりゃだめだ．

念のために相図も描いておこう．

1
2

plot(h_sq, v_sq)
plot!((h_ini, v_ini), marker = :circle, label = "initial pt")

本来は保存系であることが明白なのに、数値解は一周してもとに戻ってこない．やはりまずいねえ…

さて，アプローチ 1 の例と同様に，この Euler法も Δt を十分小さくするとまあ悪くない近似解を出すかもしれない，という期待はできる． 確かめよう．

まず，計算は以下のようになるね．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

last_T = 50
Δt = 0.001 # 2桁小さくしてみた
N = Int(last_T/Δt)

h,v = h_ini, v_ini
h_sq = [h]
v_sq = [v]
E_sq = [ energy(h,v) ]

for i in 1:N
    h,v = euler(h,v)
    push!(h_sq, h)
    push!(v_sq, v)
    push!(E_sq, energy(h,v))
end

まず近似解のプロットだ．

1

plot( h_sq )

数値解そのものはさっきよりはだいぶいいね． 誤差も見てみよう．

1
2

t_sq = Δt * [0:N]
plot(t_sq, h_sq .- h_true.( t_sq[1] ))

誤差はひどいね．こんなに Δt を小さくしたのに，h_n の値は2桁ぐらいしかあってないということだね．

エネルギーも見てみよう．

1

plot( E_sq )

さっきよりはマシだが，$E = 0.5$ から純粋にエネルギーが増大してしまっている． 相図で様子を確かめよう．

1
2

plot(h_sq, v_sq)
plot!((h_ini, v_ini), marker = :circle, label = "initial pt")

じりじりと軌道が大きくなっているようだな… 戻ってくるだけ，アプローチ1 の方がマシかな．

というわけで，いまのところ「アプローチ3 + Euler法」は以下のような感じかな．

• 理論との整合性はいいね．
• 数値計算のために式は簡単に作れる．
• プログラムも簡単だ．
• (上で言及してないが)実行速度も速いはず．
• ただ，数値解の誤差はでかいし，本質的に「悪い」．
• エネルギーなどの「系の性質」に関わる量の近似計算も悪いね．
• Δt を小さくすると誤差は小さくなるが，挙動が「戻ってこない」ので保存系の計算には向いてないね．

というわけで，この「アプローチ3 + Euler法」は正直おすすめできないかな． アプローチ 1 より悪いんじゃないかな．

Runge-Kutta 法なら？

というわけで、このアプローチの「汎用解法」の部分を Runge-Kutta 法に切り替えてみよう． つまり、もとの微分方程式を、左辺 = 一階微分 の形式に書き直した

\[ \left\{ \begin{array}{rcl} \displaystyle \frac{d h}{dt} & = & v, \cr \displaystyle \frac{d v}{dt} & = & \displaystyle -\frac{k}{m} h -g \end{array} \right. \]

に対して Runge-Kutta 法を適用するわけだ．

あとはいつもどおりなので、さくさくやってみよう．

まず、微分方程式の右辺を定義する．

1
2
3
4
5
6
7
8

function r(hv) 
    h,v = hv

    eq1 = v
    eq2 = - (k/m)*h - g

    return [ eq1, eq2 ]
end

そしてそれを元に Runge-Kutta 法を適用したものを作ってしまう．

1
2
3
4
5
6
7

function RK(hv)
    r1 = r(hv)
    r2 = r(hv + Δt/2 * r1)
    r3 = r(hv + Δt/2 * r2)
    r4 = r(hv + Δt * r3)
    return hv + (Δt/6) * (r1 + 2*r2 + 2*r3 + r4)
end

エネルギー計算式も呼び出しやすい形式にしておこう．

1

energy(hv) = energy(hv[1], hv[2])

あとは実際に計算するだけだ．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

Δt = 0.1 # 値を元に戻しておく

hv = [ h_ini, v_ini ]
hv_sq = copy(hv)
E_sq = [ energy(hv) ]

for i in 1:500
    hv = RK(hv)
    hv_sq = hcat(hv_sq, hv)
    push!(E_sq, energy(hv))
end

プロットしやすいように結果を切り出して…

1
2

h_sq = hv_sq[1, :]
v_sq = hv_sq[2, :]

プロットする．

1

plot(h_sq)

おお、これは最初から悪くない．悪くないぞ！

誤差もみてみよう．

1
2

t_sq = Δt * [0:500]
plot(t_sq, h_sq .- h_true.( t_sq[1] ))

だんだん大きくなっているのは気になるが，誤差の値は小さいね．h の値は 5桁ぐらい正しい，ということなので，うん，悪くないね．

エネルギーもプロットしよう．

1

plot(E_sq)

一方的にさがる傾向はあるが，3桁ぐらいはなんとか保っているか．Δtを小さくしたわけではないので，まあ悪くないというところかな． もう少し良くてもいいかなあとも思うが．

相図も描いてみよう．

1
2

plot(h_sq, v_sq)
plot!((h_ini, v_ini), marker = :circle, label = "initial pt")

ふむ、目で見る限り図の上では一周して戻ってきていると言ってよさそうだ．悪くないね．

というわけで「アプローチ3 + Runge-Kutta法」は，

• 理論との整合性はいいね．
• 数値計算のための式作成は簡単だ．
• プログラムも簡単だ．
• (言及してないが)実行速度は 「Euler法に比べ4倍遅いだけ」で，結構速いだろう．
• 数値解の誤差はけっこう小さいぞ．
• エネルギーなどの系の性質に関する量の近似計算も悪くない．
• 保存系だと，数値計算の状況もほぼきちんと「戻ってくる」．

という感じなので，この「アプローチ3 + Runge-Kutta法」は間違いなく「オススメの方法」だね．

アプローチ 4: 式を変形！離散化も工夫するぞ！

最後に次に考えられるアプローチは、

• 従属変数を新たに必要なだけ導入して方程式を一階常微分方程式に変形
• その常微分方程式に対する 特別な 解法を設計、適用

という手法で、これもまあ王道の一つといえよう．

この場合の 特別 というのはもちろん文脈依存なので、以下に「エネルギー保存性を再現するという意味で特別な」例を示すのでそれを見て雰囲気をつかもう．

まずは、先に示したように、 $v = dh/dt$ という従属変数を一つ新たに導入したときの全エネルギーは

\[ E(h,v) = \frac{1}{2} m v^2 + \frac{1}{2} k h^2 + mgh \]

となるはずだ．

そして、離散化版のエネルギーについては、ある時点 $t = n\Delta t$ での数値解 $h_n, v_n$ に対してやはりそっくりな式

\[ E_d(h_n, v_n) = \frac{1}{2} m v_n^2 + \frac{1}{2} k h_n^2 + mg h_n \]

であると定義しよう．

そして、天下りであるが、例えば、次のような数値計算式で近似値 $h_{n+1}, v_{n+1}$ を計算すると、$E_d$ は変化しない. つまり、$E_d(h_{n+1}, v_{n+1}) = E_d(h_n, v_n)$ となる．

\[ \left\{ \begin{array}{rcl} \displaystyle \frac{h_{n+1} - h_n}{\Delta t} & = & \displaystyle \frac{v_{n+1} + v_n}{2}, \cr \displaystyle \frac{v_{n+1} - v_n}{\Delta t} & = & \displaystyle -\frac{k}{m} \left( \frac{h_{n+1} + h_n}{2} \right) - g \end{array} \right. \]

この数値計算方法は以前も紹介した「構造保存数値解法」だ．なぜうまくいくかはそのときのレポート課題同様，考えてみよう．

こいつは幸いにも線形な式なので、キレイに変形できてしまう． やってみると、まず、簡単のために $\tau = \Delta/2$ とおいてから，

\[ \left\{ \begin{array}{rcl} \displaystyle h_{n+1} - \tau v_{n+1} & = & \displaystyle h_n + \tau v , \cr \displaystyle \frac{k}{m}\tau h_{n+1} + v_{n+1} & = & \displaystyle -\frac{k}{m}\tau h_n + v_n -2\tau g \end{array} \right. \]

となり、これは線形代数の記号では

\[ \left( \begin{array}{cc} 1 & -\tau \cr \displaystyle \frac{k}{m}\tau & 1 \end{array} \right) % \left( \begin{array}{c} h_{n+1} \cr v_{n+1} \end{array} \right) = \left( \begin{array}{cc} 1 & \tau \cr \displaystyle -\frac{k}{m}\tau & 1 \end{array} \right) \left( \begin{array}{c} h_n \cr v_n \end{array} \right) - \left( \begin{array}{c} 0 \cr 2\tau g \end{array} \right) \]

となる. よって、定数部分をわかりやすく

\[ A = \left(\begin{array}{cc} 1 & -\tau \cr \displaystyle \frac{k}{m}\tau & 1 \end{array}\right), \]

\[ B = \left(\begin{array}{cc} 1 & \tau \cr \displaystyle -\frac{k}{m}\tau & 1 \end{array}\right), \]

\[ \boldsymbol{b} = \left(\begin{array}{c} 0 \cr 2\tau g \end{array}\right) \]

とおくと、この数値計算式は

\[ A \, \left( \begin{array}{c} h_{n+1} \cr v_{n+1} \end{array} \right) = B \, \left( \begin{array}{c} h_n \cr v_n \end{array}\right) - \boldsymbol{b} \]

という、連立一次方程式で書けることになる． 計算上，右辺は既知のベクトルになるので，この連立一次方程式を解けば $(h_{n+1}, v_{n+1})$ が手に入るというシンプルな形であることがわかる．

さてあとはプログラムだ．

まず必要な記号の定義をしよう． 行列やベクトルは、下記のように、手書きの数式と同じように書いておくと紛れがないのでなるべくそうしよう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

τ = Δt/2

A = [ 1       -τ
     (k*τ)/m   1 ]

B = [ 1        τ
      -(k*τ)/m 1 ]

b = [ 0
      2τ*g ]

すると、この近似計算式の 1step 分はいきなり次のように書けてしまう．

1

onestep(hv) = A \ (B*hv - b)

逆行列 $A^{-1}$ を使っていないことに注意しよう．連立一次方程式を解いて答えを求めるために逆行列を計算するのは愚の骨頂というもので、理由がない限りやってはいけない．スカラーの場合だって、$24 / 3 = 24 * 0.333333.. = 8$ なんて計算手順だと計算量も多いし不要な誤差も入ってくるのがわかるだろう？

さて、あとはいつものように計算するだけだ．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

Δt = 0.1 # 念の為に

hv = [ h_ini, v_ini ]
hv_sq = copy(hv)
E_sq = [ energy(hv) ]

for i in 1:500
    hv = onestep(hv)
    hv_sq = hcat(hv_sq, hv)
    push!(E_sq, energy(hv))
end

プロット用にデータを切り出して、

1
2

h_sq = hv_sq[1, :]
v_sq = hv_sq[2, :]

まずは近似解そのものをプロット．

1

plot(h_sq)

うむ．まあうまくいっているようだな．

誤差もみてみよう．

1
2

t_sq = Δt * [0:500]
plot(t_sq, h_sq .- h_true.( t_sq[1] ))

う～ん，誤差についてはあまり良くないね．h としては2桁ぐらいしか合ってないね．

ではエネルギーはどうだろう．

1

plot(E_sq)

GKS: Possible loss of precision in routine SET_WINDOW

値の変化が乏しすぎてプロットに警告が出ている． というわけで初期値からのズレをプロットさせよう．

1

plot( E_sq .- E_sq[1] )

おお！ エネルギー値は 11桁ほど保たれているぞ．ふむ、これは良い．

そして少し面白い．というのも, 数値解としては厳密解からそれなりにずれているのに，エネルギー値はほぼ正しく保存している，ということだからねえ．

一応、相図もプロットしておこう．明らかに，目で見る範囲ではきれいに戻ってくると思うぞ．

1
2

plot(h_sq, v_sq)
plot!((h_ini, v_ini), marker = :circle, label = "initial pt")

というわけで、このアプローチ4の「構造保存数値解法」だと不思議な良さがあるね．こんな感じだ．

• 理論との整合性はいいね．
• 数値計算のための式作成はどうなっている？ (考えてみよう)
• プログラムはまあ簡単な方かな．
• (言及してないが)実行速度は少し遅そうだ．非線形問題なら非線形連立方程式を解く必要があるからね．
• 数値解の誤差はそんなに小さいわけではないね．
• エネルギーなどの系の性質に関する量の近似計算はびっくりするぐらい良い．
• 保存系だと，数値計算の状況もきちんと「戻ってくる」．

という感じなので，この「アプローチ4」もまあ「オススメ」して良さそうかな．

問題はどうやってこの謎の近似式を作成するか，だね． それには構造保存数値解法の勉強が必要なので，検索してみるといいだろう．