00.数値計算の 2つの有限性 • Daisuke Furihata (降籏大介)

コンピュータ計算の「二つの有限性と誤差」

数値解析とは大雑把に言って「数学で書かれた問題をコンピュータで具体例を計算する」もの．その際，まあ一般的に 2種類の誤差が発生するのだ．

それを，積分 \[ I \defeq \int_a^b f(x) dx \] の代わりに，下記の台形則で近似計算して $I_d$ を求めるという例を通じて説明しよう． \[ I_d \defeq \left\{ \half f_0 + \sum_{k=1}^{N-1} f_k + \half f_N \right\} \Delta x , \] ただし，$N$ は正整数で，$\Delta x \defeq (b-a)/N$, $f_k \defeq f(a + k\Delta x)$ だ．

この近似を図にすると

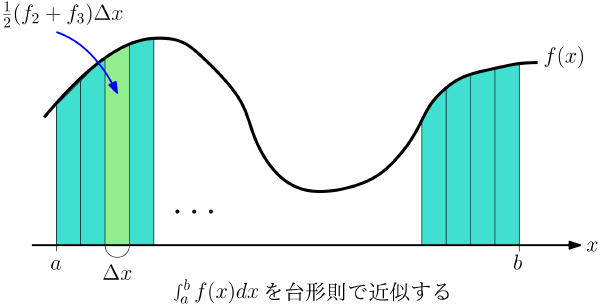
という感じだ．図中の台形の面積を足し合わせて，全体積分の近似とするというやつだな．

さてこのとき，全体の計算誤差は $I - I_d$ だと思うだろ？違うんだ．それでは足りない.

実は，$I_d$ を計算する過程において，$f_k$ を求めるときや，それらの足し算をするとき，そして $\Delta x$ を掛けるときにも誤差が発生するのだ．

だから，コンピュータで計算して実際に求まる $I_d$ の値を $I_d^{\dagger}$ と書いて区別して，全体の誤差を $\epsilon$ とすると \[ \epsilon \defeq \left| I_d^{\dagger} - I \right| \] と定義されることになる．これは \[ \epsilon = \left| I_d^{\dagger} - I \right| = \left| {\color{red} I_d^{\dagger} - I_d} + {\color{blue} I_d - I} \right| \] と書き換えることができて，それぞれ誤差の由来別(後述)に ${\color{red} I_d^{\dagger} - I_d}$ と ${\color{blue} I_d - I}$ とを考えることができる．

この問題の場合，これらはそれぞれ次のような評価ができる(詳細は省略だ).

\begin{eqnarray} {\color{red} I_d^{\dagger} - I_d} & \cong & O(N), \cr {\color{blue} I_d - I} & \cong & O(1/N^2) \end{eqnarray}

ということは計算量 $N$ を増やすと ${\color{red} I_d^{\dagger} - I_d}$ が増えてしまうし，計算量 $N$ を減らすと ${\color{blue} I_d - I}$ が増えてしまう．

つまり，この例の場合，

計算量をあまり増やしても減らしても良くない

のだ．これは

誤差を一番小さくする適切な計算量がある

ことを意味していて，そして

誤差を無限にゼロに近づけていくことは原理的に出来ない

ことさえ意味している．

そして，この例はかなり一般化できて，上の2つの誤差は以下のような(名前と)性質を持っているのだ．

丸め誤差: 上の例では ${\color{red} I_d^{\dagger} - I_d}$ にあたる誤差．計算過程それぞれで計算結果が「メモリで用意した桁数を超えてしまい，その分の情報を切り捨てる」ことによって発生する誤差．

計算機のメモリが有限であり，実数を格納できないため起きる誤差

と言える．
計算一回ごとに丸め誤差が発生するので，全体の計算量が増えると当然丸め誤差は蓄積して大きくなってしまう．
打切り誤差: 上の例では ${\color{blue} I_d - I}$ にあたる誤差．連続的な数式を，コンピュータで実際に計算可能な有限の計算量の近似式で置き換えることによって発生する誤差．

計算機の計算速度が有限であり，極限が計算できないため起きる誤差

と言える．
計算回数を増やして極限に近づけば小さくなるタイプの誤差であるので，計算量が増えると打ち切り誤差は小さくなる．

全体の誤差はこの合計に相当するので，上の例同様，下図のような関係になる．

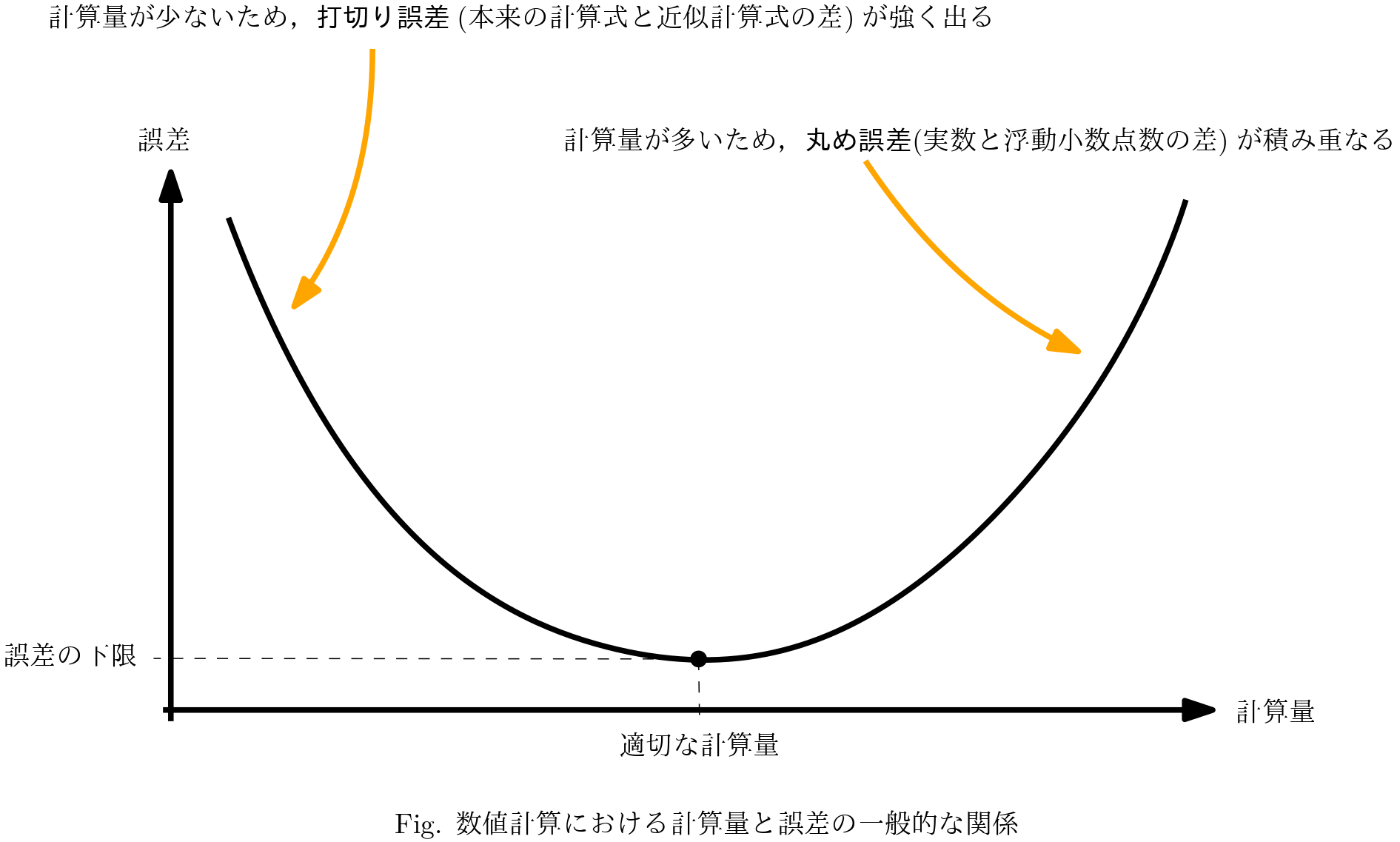
つまり，計算機をぶん回して大量に計算すれば良いというものではなくて，「近似計算方法を定めると，それによる誤差の下限と，それを達成する適切な計算回数が定まってしまう」という一般的な関係があるのだ．

しかもこれは上で述べた計算機がもつ2つの有限性に依るものなので，いまのところこの一般論を変えることは原理的に不可能だ¹．

だからわれわれは，なにも考えずに計算するのではなく，「なるべく適切な近似計算方法」を考案・選択し，「この誤差曲線を下げる」という，そもそも論を考えないといけない．それには結局「数学的にきちんと考える」ということが必要で，「計算機が速くても、結局は使う人間の数学的能力が効いてきちゃうよ」というお話になってしまう．

この授業では，こうした背景をもとに，コンピュータで数学的な対象の具体例を計算するにあたってどのように考え，プログラムをしていけばよいか，を学んでいくこととなる．

原理的に計算速度が無限だとも言える量子コンピュータには期待しているけれども，われわれが生きているうちに実用レベルに達するだろうか… ↩︎