Volterra の被食者-捕食者モデル方程式の計算にチャレンジ

前回まで大変シンプルな，単独のスカラー値常微分方程式を対象としてきた．まあ悪くなかったが，解もシンプルでちょっとつまらないと感じた人も居ただろう．

そこで，今回は，挙動もそれなりに興味深い連立常微分方程式である Volterra の被食者-捕食者モデル方程式を対象として数値計算に取り組んでみよう．

対象問題はスカラー値常微分方程式 → 連立常微分方程式 → 偏微分方程式という流れでつながる．まあそういうもうのか、と思って今はこの流れについていこう．

さて、以前モデリングのところで紹介したように、Volterra の被食者-捕食者モデル方程式は、時間変数を $t$, 被食者数を関数 $u(t)$ で、捕食者数を関数 $v(t)$ で表すとして以下のような非線形の常微分微分方程式で表されるものだった．

\[ \left\{\begin{array}{rcl} \displaystyle \frac{du}{dt} & = & - C_1 \, uv + D_1 \, u, \cr \displaystyle \frac{dv}{dt} & = & C_2 \, uv - D_2 \, v . \end{array}\right. \]

ただし、わかりやすいように、係数 $C_1$, $C_2$, $D_1$, $D_2$ は全て定数で、かつ、正の値であるとして考えよう．

このモデル方程式に従って計算するとどうなるか、たいへん大雑把なところは以前解説したが、今回はこれを自分で実際に計算してみよう．

まあまずは簡単な Euler 法で

離散時間の近似解を $u_n \cong u(n\Delta t)$, $v_n \cong v(n\Delta t)$, と書くとして、Euler スキームは次のようになるだろう．

\[ \left\{\begin{array}{rcl} \displaystyle \frac{u_{n+1} - u_n}{\Delta t} & = & - C_1\, u_n v_n + D_1\, u_n , \cr \displaystyle \frac{v_{n+1} - v_n}{\Delta t} & = & C_2\, u_n v_n - D_2\, v_n . \end{array}\right. \]

これを変形してプログラムの中で使いやすい形、つまり、新しい値 = 古い値による計算 という形に直すと次のようになる．

\[ \left\{\begin{array}{rcl} u_{n+1} & = & \left(1 + \Delta t \left( D_1 - C_1 v_n \right) \right)\, u_n , \cr % v_{n+1} & = & \left(1 + \Delta t \left( - D_2 + C_2 u_n \right) \right)\, v_n . \end{array}\right. \]

というわけで Euler 法による近似式はこれでよさそうだ．

次に、用いる定数だが、とりあえず $C_1 = $ $C_2 = $ $D_1 = $ $D_2 = 1.0$, $u(0) = v(0) = 0.7$, としておこう．あとは、近似のために発生したパラメータ $\Delta t$ だが、まあ最初は $\Delta t = 0.05$ ぐらいでやってみよう．

では、プログラムだ．まず定数を設定して、

1
2
3


C1 = C2 = D1 = D2 = 1.0
u0 = v0 = 0.7
Δt = 0.05

次に、Euler スキームによる時間 1ステップ分の発展を関数として定義する．

1
2
3
4
5


function euler(u,v)
    u_new = (1 + Δt * (  D1 - C1*v ) ) * u
    v_new = (1 + Δt * ( -D2 + C2*u ) ) * v
    return u_new, v_new 
end

早速、初期値を試しに入れて、動作するかどうか確かめてみよう

1

euler(u0,v0)

 (0.7104999999999999, 0.6895)

とりあえず動きそうなので,思い切って 500ステップほど動かしてみようか．

1
2
3
4
5
6
7


u,v = u0, v0        # 初期値を入れて…
uv_sq = [ u0 v0 ]  # グラフを描きたいので、データをとっておこう

for i in 1:500
    u,v = euler(u,v)
    uv_sq = vcat(uv_sq, [ u v ])  # データを追加
end

結果がきちんと出ているか、単純に数字をまずちょっと眺めてみよう．

1

uv_sq

501×2 Array{Float64,2}:
0.7       0.7
0.7105    0.6895
0.721531  0.679519
0.733092  0.670058
…略…
0.355027  1.07067
0.353772  1.03614
0.353133  1.00266
0.353086  0.970234

うん、結果が数字として出ていて，エラーにはなっていないようだ．では、早速グラフで様子を見てみよう．

1
2
3
4
5
6
7
8


using Plots

default( legend = :outertopright, xlabel = "time t", ylabel = "number" )

t_sq = Δt * [0:500]
plot(t_sq, uv_sq, label = ["魚 🐟" "鮫 🦈"], fontfamily="Meiryo" )
# 上の fontfamily = は絵文字対応フォント指定(Windowsの場合)．
# MacOS の場合は Hiragino かな？

svg

青線が $u_n$ (魚 🐟 に相当)で、赤線が $v_n$ (サメ 🦈 に相当)だね．

さて、計算結果の内容をチェックしよう．グラフをみるとだんだん振幅が大きくなっているけどこの挙動は信用して良いものだろうか？

こういうときは，計算結果に影響を与えそうなパラメータをいじってみるとよい．今回の場合，$\Delta t$ を小さくして、全体の様子が変化しないかチェックしてみるということになるね．

上のグラフと比べたいので、同じ時間( $t=25.0$ )ぐらいまで計算することにしよう．すると次のような感じかな．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


lastT = 25   # 計算を終える時間(おおよそ)を設定．
Δt = 0.01    # Δt をさっきの 1/5 と，小さめに設定し直す．
N = round(Int, lastT/Δt)   # 最終時間ステップは整数に．

# 計算ステップ数を N に直し，あとは前と同様に．
u,v = u0, v0
uv_sq = [ u0 v0 ]

for i in 1:N
    u,v = euler(u,v)
    uv_sq = vcat(uv_sq, [ u v ])
end

として計算して、グラフを早速描いてみる．

1
2


t_sq = Δt * [0:N]
plot(t_sq, uv_sq, label = ["魚 🐟" "鮫 🦈"], fontfamily="Meiryo" )

svg

んん？随分変わってしまったな．振幅が余り変わらなくなった．どうやら, 以前同様にこの問題でも Euler スキームは ($\Delta t$ が大きい時はとくに)信用ならないようだ．あとでもう少し信用できそうな方法で計算し直そう(→ レポート問題).

相図をみてみよう

(以前も紹介したが)相図というのは，系の状況を表す従属変数「のみ」で描いたグラフを言う．

今確認したように Euler 法の結果はあまり信用ならないけれども、$\Delta t$ が小さいならばまあまったく外れというわけでもなさそうなので、まずはこの Euler 法の結果を使って相図を作り、様子を見てみよう．なにか見えてくるものがあるかもしれない．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


u_sq = uv_sq[:,1] # データの 1列目 = 魚の近似値の列．
v_sq = uv_sq[:,2] # データの 2列目 = サメの近似値の列．

plot(u_sq, v_sq)
plot!((u0,v0), marker = :circle, fontfamily="Meiryo",
  aspect_ratio = 1, legend = false,
  xaxis = "魚 🐟", yaxis = "鮫 🦈" )
# aspect_ratio は縦横の軸の比率．

annotate!(u0,v0, ("初期値", :bottom, :left)) # 好きな場所に注釈を書ける

svg

どうやら、相図の上では、ぐるぐると反時計回りに周っている状態のようだ．円とはすこし違った歪んだ形のようではあるが．

相図上の軌道の形

ちなみに、この「ぐるぐる周っている軌道」の形、つまり、軌道を数式で表す方法などは理論的にわかるものなのだろうか？それがわかれば，系の挙動が数式で陽に表せたということになり，未来も厳密に予測できるなど，得られるものは多いだろう．

実は、一般に、相図上の軌道を式で表すことは数学的になかなか難しい問題で、「初等関数では表せないことが証明されている」ようなケースも有るぐらいだ．

そしてさらに、この Volterra モデルの場合は「大変ラッキーなことに」この軌道を数式できちんと書けるのだ！詳しいことは次回の授業で少しまじめに解説しよう．

漁業の影響を見てみよう

さて，この Volterra モデルは漁業の影響をうまく説明したものだった．それをみてみよう．これがこのモデルのいちばん重要なポイントであるので、丁寧に考えながらやろう．

まず、モデルの数式は、漁業の影響係数 $E > 0$ を用いて、漁業「有り」だと次のようになると考えるとよさそうだ、と Volterra さんは考えた．

\[ \left\{\begin{array}{rcl} \displaystyle \frac{du}{dt} & = & - C_1\, uv + D_1\, u - E\, u, \cr \displaystyle \frac{dv}{dt} & = & C_2\, uv - D_2\, v - E\, v . \end{array}\right. \]

そこで、この数式をやはり近似して、計算してみよう．

なお、この係数 $E$ はとりあえず $E = 0.5$ としておこう．

Euler 法で…

先の Eulerスキームを一部変えるだけでいいはずだ．次のようになるだろう．

\[ \left\{\begin{array}{rcl} \displaystyle \frac{u_{n+1} - u_n}{\Delta t} & = & - C_1 u_n v_n + D_1 u_n - E u_n, \cr \displaystyle \frac{v_{n+1} - v_n}{\Delta t} & = & C_2 u_n v_n - D_2 v_n - E v_n . \end{array}\right. \]

先と同様に、プログラムに使いやすいように書き直すとたとえば次のようになるだろう．

\[ \left\{\begin{array}{rcl} u_{n+1} & = & \left(1 + \Delta t \left( D_1 - E - C_1 v_n \right) \right)\, u_n, \cr % v_{n+1} & = & \left(1 + \Delta t \left( - D_2 - E + C_2 u_n \right) \right)\, v_n . \end{array}\right. \]

実際にその 1ステップ分を関数としてプログラムすると以下のような感じになるだろう．

1
2
3
4
5


function euler_fishing(u,v,E)
    u_new = (1 + Δt * (  D1 - E - C1*v ) ) * u
    v_new = (1 + Δt * ( -D2 - E + C2*u ) ) * v
    return u_new, v_new
end

実際に動かしてみよう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


E = 0.5

lastT = 25
Δt = 0.01
N = round(Int, lastT/Δt)   # 最終時間ステップは整数に．

u,v = u0, v0
uv_f_sq = [ u0 v0 ]

for i in 1:N
    u,v = euler_fishing(u,v,E)
    uv_f_sq = vcat(uv_f_sq, [ u v ])
end

無事に動いたら、これを早速グラフで見てみよう．

1
2


t_sq = Δt * [0:N]
plot(t_sq, uv_f_sq, label = ["魚 🐟" "鮫 🦈"], fontfamily="Meiryo" )

svg

んんん？これは随分変わったな．早速相図を描いてみよう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


u_f_sq = uv_f_sq[:,1]
v_f_sq = uv_f_sq[:,2]

default(aspect_ratio = 1, legend = false,
  xaxis = "魚 🐟", yaxis = "鮫 🦈", fontfamily = "Meiryo" )
# 以降，楽をするためにデフォルト設定してしまえ．

plot(u_f_sq, v_f_sq)
plot!((u0,v0), marker = :circle)
annotate!( u0, v0, ("初期値", :top, :left))

svg

おお，だいぶ変わったな．

さらによく見て見るために，比べてみよう．変化を見たいので、漁業効果の入っていないデータと一緒に描いてみよう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


default( legend = :outertopright )

# 漁業効果無しのケースをプロットして、
plot(u_sq, v_sq, label = "漁業無し")

# 次に漁業効果有りのケースを描き足して、
plot!(u_f_sq, v_f_sq, label = "漁業有り")

# 初期値も描き足す
plot!((u0,v0), marker = :circle, label = false )
annotate!( u0, v0, ("初期値", :left))

svg

以前の授業で解説したように，漁業が行われると、相図の上での軌跡の中心が右下にずれる ことがわかる．ついでに、軌跡も大きくなるようだ．

これは、モデルの説明のときにも示したように、

「漁業を行うと魚の量がかえって増える現象」をうまく説明できている

ようにみえ、Volterra モデルの妥当性を示していると言える．

さて、じつは、もとの Volterra モデルの常微分方程式の不動点(時間変化しない (u,v)点)は、この「軌跡の中心」とでもいうべき点なのだ．というのも，この方程式では，軌道の「平均」を計算すると，この不動点と一致するのだ．

チャレンジ: それぞれの軌道の中心点相当である不動点を，モデルの常微分方程式から導出してみよう(答えはすぐ下)．

さて，この軌道中心点相当である不動点は、それぞれのケースで実際に計算すると

漁業なし… 中心 $\displaystyle = \left(\frac{D_2}{C_2}, \frac{D_1}{C_1}\right)$,

漁業あり… 中心 $\displaystyle = \left(\frac{D_2 + E}{C_2}, \frac{D_1 - E}{C_1}\right)$

となる．そこでこれも相図に描き込んでみよう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


plot(u_sq, v_sq, label = "漁業無し")

# 次に漁業効果有りのケースを描き足して、
plot!(u_f_sq, v_f_sq, label = "漁業有り")

# 初期値
plot!((u0,v0), marker = :circle, label = false )
annotate!( u0, v0, ("初期値", :left))

# それぞれの軌道中心
plot!((D2/C2,D1/C1), marker = :circle, label = false)
annotate!( D2/C2,D1/C1, ("中心", :left))

plot!(((D2 + E)/C2,(D1 - E)/C1), marker = :circle, label = false )
annotate!( (D2 + E)/C2, (D1 - E)/C1, ("中心", :left))

svg

なんとなく、いろいろと分かってきたようなきがするのではないだろうか．

かなりグラフが「ダサく」なってきた．自分でもっとかっこいいグラフにしておこう．

リアルタイムに漁業の影響の大きさをいろいろ変えて、相図の様子の変化をみてみよう

Interact package を使うとパラメータをマウスで変化させつつリアルタイム処理ができる．これを使って、漁業の影響をグラフで直接みてみよう．

まずは Package の使用宣言だ．

1

using Interact

Interact の使い方は以前示したように @manipulate マクロに続けて for 文を書けば良い．今回の場合はまず以下のようにしてみよう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


default( ylims = (-0.5, 4.5), aspect_ratio = :none,
   xlabel = "time t", ylabel = "number" )
# グラフの描画範囲を統一することで見やすくする．
# この数字は，教官がさきにおおよそ計算したおいたもの．

@manipulate for E in 0.0:0.01:0.8

    # ここから end まではこれまでと本質的に同じ．
    u,v = u0, v0
    uv_f_sq = [ u0 v0 ]
    
    for i in 1:N
        u,v = euler_fishing(u,v,E)
        uv_f_sq = vcat(uv_f_sq, [ u v ])
    end

    plot(t_sq, uv_f_sq, label = ["魚 🐟" "鮫 🦈"], fontfamily="Meiryo" )
end

すると，下図のようにマウスで漁業係数 $E$ をコントロールできるバーが jupyter 上に現れるので，これを動かして，漁業効果の大小で全体の挙動がどう変わるか見てみよう．

バーを掴んで動かしていろいろ見てみると，下記のようなことがわかってくる．

漁業の影響が多少ならば、魚も増えてサメも減り，良いことばかりのように見えるが…
漁業の影響が強くなると「全体挙動の時間周期が長くなる」ため，漁業的には「不漁と大漁」の間の期間が長くなり，経済的にも不安定に
漁業の影響が強くなると「サメの数の最小値が小さくなりゼロに近づく」「サメが減りすぎる期間が大きくなる」ことからサメの絶滅が危惧される．これは魚増殖のブレーキがなくなることなので，「魚が増えすぎて環境破壊へ」という危険性の増大を意味する．
そう，直感と異なり，漁業は魚ではなくサメの絶滅をもたらしかねないのだ．

など，漁業による思わぬ影響が見えてくるだろう¹．

さて、@manipulate のところを @gif と変えるだけで、今度はアニメーションを作ることが出来る．やってみよう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


@gif for E in 0.0:0.01:0.8

    # ここから end まではこれまでと本質的に同じ．
    u,v = u0, v0
    uv_f_sq = [ u0 v0 ]
    
    for i in 1:N
        u,v = euler_fishing(u,v,E)
        uv_f_sq = vcat(uv_f_sq, [ u v ])
    end

    plot(t_sq, uv_f_sq, label = ["fish" "shark"] )
    # @gif マクロは font に対してあまり自由度はないようなので alphabet 表記で．

    annotate!(2.5, 4.0, ("E = $E", :left))
    # 漁業効果の強さも表示しておく
end

すると，

┌ Info: Saved animation to 
│   fn = c:\home\julia-programs\v1.6\tmp.gif
└ @ Plots c:\julia\PKG\v1.6\packages\Plots\1RWWg\src\animation.jl:114

といったようなメッセージが出ることから，tmp.gif という名前で gif ファイルがどのフォルダにできているかがわかる．中身は下のようになっているだろう．

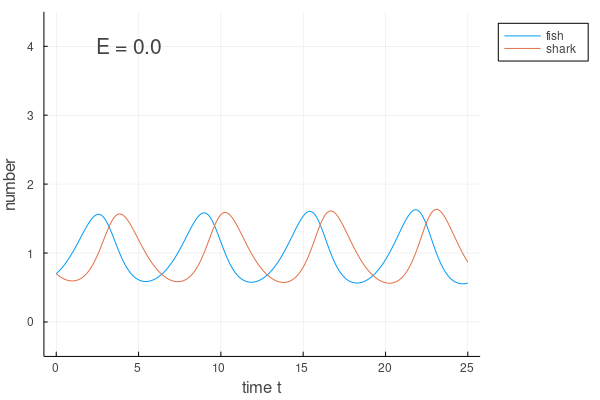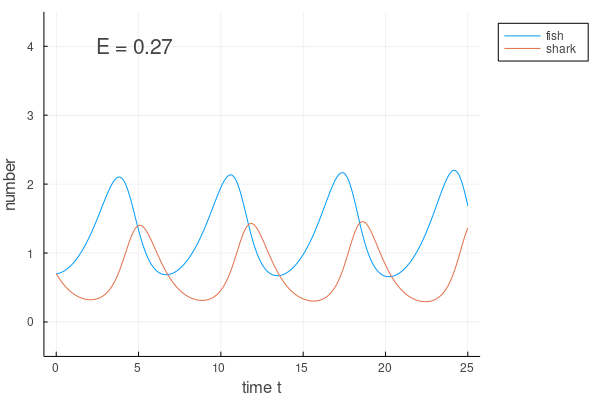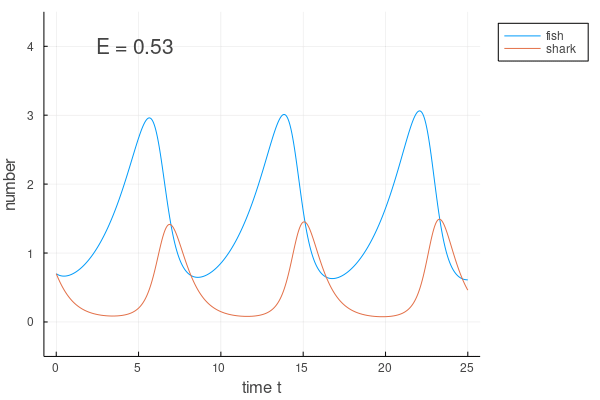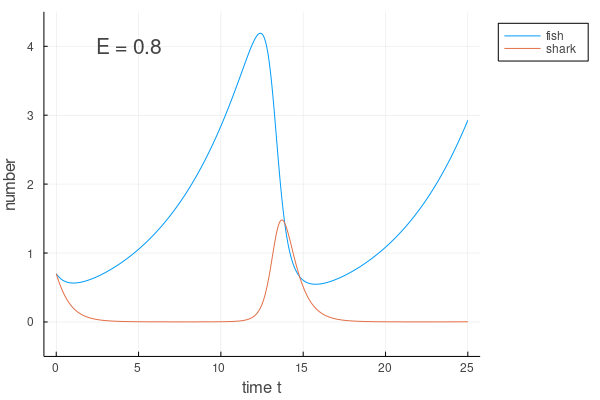
シチュエーションによっては、こうしたアニメーションのほうが様子を上手く掴めたりするので、上手に使っていくとよいだろう．

相図も同様に，@manipulate等の作業をやってみよう．以下のような感じだ．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


default( xlims = (0.3, 4.5), ylims = (0.0, 1.8),
  xlabel = "fish", ylabel = "shark",
  legend = :topright )
# グラフの描画範囲を統一することで見やすくする．
# この数字は，さきにおおよそ教官が計算したおいたものによる．

@manipulate for E in 0.0:0.01:0.8

    # ここから end まではこれまでと本質的に同じ．
    u,v = u0, v0
    uv_f_sq = [ u0 v0 ]
    
    for i in 1:N
        u,v = euler_fishing(u,v,E)
        uv_f_sq = vcat(uv_f_sq, [ u v ])
    end
    
    u_f_sq = uv_f_sq[:,1]
    v_f_sq = uv_f_sq[:,2]
    
    plot(u_sq, v_sq, label = "漁業無し")
    plot!(u_f_sq, v_f_sq, label = "漁業有り")
    plot!((u0,v0), marker = :star, lab = "初期値")
    plot!((D2/C2,D1/C1), marker = :circle, label = false ) 
    plot!(((D2 + E)/C2,(D1 - E)/C1), marker = :circle, label = false ) 
end

これも同様に，@manipulate を @gif に変えてアニメーションを作ってみよう．
ただし，日本語等のフォントはやはり選べないと思うので，label はアルファベット表記にしておこう．

レポート

下記要領でレポートを出してみよう．

e-mail にて，
題名を 2021-numerical-analysis-report-07 として,
教官宛(アドレスは web の "TOP" を見よう)に，
自分の学籍番号と名前を必ず書き込んで，
内容はテキストでも良いし，pdf などの電子ファイルを添付しても良いので，

下記の内容を実行して，結果や解析，感想等をレポートとして提出しよう．

漁業効果無し，有りの両方の Volterraモデルに対して、時間方向に対称なスキームを自分で作って計算してみよう．

この問題で時間対称なスキームを作ると、時間ステップを 1ステップ進めるのに連立非線形方程式を解かないといけない形になるはずだ．その解法にもしも Newton 法を使おうとすると、スカラー値常微分方程式よりも少しばかり手強いかもしれない．そうした場合は、Newton 法よりも NLsolve package を使ったほうが楽だろうね．
同様に，漁業効果無し，有りの両方で、Runge-Kutta スキームを自分で作って計算してみよう．

やってみるとわかるが、時間方向に対称なスキームを作ることに比べると Runge-Kutta 法を用いることは格段に容易だ．実感しよう．
上の2つの計算方法による数値解それぞれに対して相図をつくり，軌道がどのようになっているか，Euler 法の相図と比べてみよう．

もちろん，あくまで「モデルが正しいと仮定するならば」という前提のもとでの話だ． ↩︎

数値計算法基礎 (2021)

07. 連立常微分方程式にチャレンジ