sample: 構造保存数値解法

さて，sample コード: Euler 法 と同じ問題について、今度は構造保存数値スキームを作ってみるぜ． 数値計算での構造保存ってのは，元の問題が持つ数学的な性質を数値計算でもきちんと再現しよう！ ってことの謂で，その着目する性質の背景，つまり，数学的な構造を数値計算で再現することになるんでこう呼ばれるのよ．

さて，堅苦しいことはともかく，まずは対象となる「方程式の構造」とやらを探ってみるか．

散逸性，保存性

面倒なことはまあおいといて，解のもつ保存量やら散逸量やらをチェックしてみればまあ悪く無いやろ，ということで，その方向で調べてみよう．

幸い、この偏微分方程式は以下のように変数変換すると、その性質がわかりやすい形に変形できる． まず、両辺を $u$ で割ると \begin{equation} \mbox{ もとの偏微分方程式 } \Longleftrightarrow \frac{1}{u} \pdrv{u}{t} = \pdrv{^2 u}{x^2} \end{equation} となるが、左辺については \begin{equation} \frac{1}{u} \pdrv{u}{t} = \pdrv{}{t} \left( \log(u) \right) \end{equation} であるので、$v = \log(u) $ とおくと見通しが良くなりそうやね． よって、そうしよう． すると， \begin{equation} \mbox{ もとの偏微分方程式 } \Longleftrightarrow \pdrv{v}{t} = \pdrv{^2 \left( e^v \right) }{x^2} \end{equation} となる． そして、明らかに、変分導関数に対して \begin{equation} e^v = \ddrv{ \left( e^v \right) }{v} \end{equation} であるので、結局、 \begin{equation} \mbox{ もとの偏微分方程式 } \Longleftrightarrow \pdrv{v}{t} = \pdrv{^2}{x^2} \left( \ddrv{ \left( e^v \right) }{v} \right) \label{eq:structure-pde} \end{equation} となる． すると、次の量

1. $ I[v] \mbox{ } \defeq \mbox{ } \int_0^L e^v \dx, $
2. $ M[v] \mbox{ } \defeq \mbox{ } \int_0^L v \dx $

に対して，自動的に一般に以下のことが言える．

1. $ I[v] $ は本質的に散逸量である
2. $ M[v] $ は本質的に保存量である

「本質的に」ってのは，大雑把に言えば，境界項を無視して，っつう意味やね． 今回のノイマン境界条件の場合はこのストーリーで出てくる境界項は全部消えてしまうので，掛け値なしにこれらは散逸量/保存量なわけだ．

確かにこれらのことが言えることは、念の為に話を $ u $ の表現に戻して次のように計算して確かめられる(もちろん $ v $ でやっても良い)． \begin{equation} \drv{}{t} I[u] = \int \pdrv{u}{t} \dx = \int u \pdrv{^2 u}{x^2} \dx = \left[ u \pdrv{u}{x} \right]_0^L - \int \left( \pdrv{u}{x} \right)^2 \dx = - \int \left( \pdrv{u}{x} \right)^2 \dx \leq 0. \end{equation}

\begin{equation} \drv{}{t} M[u] = \int \pdrv{}{t} \log(u) \dx = \int \frac{1}{u} \pdrv{u}{t}\dx = \int \pdrv{^2 u}{x^2} \dx = \left[ \pdrv{u}{x} \right]_0^L = 0. \end{equation}

というわけで，この問題が持つ散逸量と保存量がこうやって見つかったわけだ． よって、素直に考えれば，これらの散逸性、保存性を再現するような数値解法をデザインすることが構造保存解法として狙うモノ，ってことになるかな．

構造保存数値スキーム

上で見つけた散逸性と保存性は，数学的には，方程式が式 $(\ref{eq:structure-pde})$ の形で書かれていることに起因するんだな． こういう風に方程式が変分導関数で記述されていることによって示される散逸性や保存性は，数値計算で再現することができる． その方法は離散変分導関数法って呼ばれてるが，まあ，この名前は長いから，これより後はこれを Discrete Variational Derivative Method の頭文字をつなげて DVDM と呼ぶぜ．

さて，DVDM のご託宣に従えば，この場合最も実直な DVDM スキームは

\begin{equation} \frac{\vP - \v}{\Dt} = \dd{k}{2} \left( \drv{e^v}{(\vP,\v)} \right), \mbox{ ただし } \v \defeq \log(\u) \label{eq:dvdm-scheme} \end{equation}

ってことになるな． ちなみに右辺の $d/d()$ ってのは差分商ってやつで，関数 $f(x)$ に対して

\begin{eqnarray} \drv{f}{(a,b)} & \defeq & \frac{f(a) - f(b)}{a-b}, \mbox{ when } a \neq b, \newline % & \defeq & \left.\drv{f}{x}\right|_{x=a}, \mbox{ when } a = b \end{eqnarray}

が定義になるかな．

境界条件の離散化については sample: Euler 法 に書いたものと同じでいい． そしてこのとき、このスキーム $(\ref{eq:dvdm-scheme})$ は $I, M$ の離散版

\begin{eqnarray} \mbox{散逸量 } I_d [\bm{u}^{(n)}] & \defeq & {\sum_{k=0}^N}” \u \Dx , \newline \mbox{保存量 } M_d [\bm{u}^{(n)}] & \defeq & {\sum_{k=0}^N}” \log(\u) \Dx \end{eqnarray}

について、その散逸性と保存性を保つ、っちゅうわけだ． ちなみに ${\sum}” $ ってのは台形則やね．足すときに、端っこの値だけ $ 1 / 2 $ を掛けるってやつだ．

まあ、こうしたストーリについて、詳しくは DVDM がらみの解説でも探して読んでくれ．

あと、式 $(\ref{eq:dvdm-scheme})$ を $u$ の式に書きなおして，

\begin{equation} \frac{\log(\uP) - \log(\u)}{\Dt} = \dd{k}{2} \left( \frac{\uP - \u }{\log(\uP) - \log(\u)} \right) \end{equation}

という感じにしてこれで計算してもいいかもしれんな． まあ今回は 式 $(\ref{eq:dvdm-scheme})$ の方が素直な形なので，これでプログラムしてみよう．

プログラム

さて，上の式 $(\ref{eq:dvdm-scheme})$ をほぼそのままプログラムにしてみると次のような感じになる． こんな簡単に書いて動くものなのかしらん．

###
using ForwardDiff

### 各種パラメータ
const L = 2.0
const N = 200
const Dx = L/N

const T = 1.0
const Dt = 10.0^(-3)
const N_time = Int(round(T/Dt))
const skip_time = div(N_time,10)

const gamma_r = Dt/(Dx^2)

const data_fname = "data.dat"
const I_fname    = "I.dat"
const M_fname    = "M.dat"

const Newton_Criterion = 10.0^(-6)

### 注意: 次のマクロについては素人は理解できなくても問題ないので、内容は気にしなくて良い．
###       こうすると「素直にプログラムが書けて」「バグが出る可能性を減らせる」だけの話．
###
### Julia 言語での配列の添字は 1 からだが、数式での離散関数の添字は(境界端がゼロなため) 0 からになる．
### このズレに基づくトラブルに悩まされないように、離散関数 u(k) = (プログラム) @U(u,k) = 配列 u[k+1] となるようにマクロ @U を用意する．
### マクロは結果ではなくて式を返すので、この @U(u,k) は実行前に u[k+1] そのものに変換される．つまり、「代入も可能」である!
macro U(v, k)
  # Expr(:ref, v, eval( eval(k) + 1 ) ) でもいいが、ちょっとだけ遅いかも(測定できないと思うが). まあ好みの範囲．
  Expr(:ref, v, Expr(:call, +, k, 1) )
end

### 初期値を決める関数．境界条件に合っている．
function u0(x)
  A0 = 1.0; A1 = 2.0; B2 = 0.3;
  A0 + A1 - A1 * cos(pi*x/L) + B2*cos(2*pi*2x/L)
  end

### 近似解の値の出力. こういうのは用意しておくと良いねえ．
function result_out(v, time, data_f, I_f, M_f)
  println(data_f, "\n## time = $(time)")

  for k in 0:N
    println(data_f, @U(v,k) )
  end

  println(I_f, time, " ", I(v) )
  println(M_f, time, " ", M(v) )

end

### 散逸量 I[u] を計算する．
function I(v)
  I = sum(v) # いったん全部足して、
  I = I - 0.5*( @U(v,0) + @U(v,N)) # 台形則なので一番端の重みは半分．
  return Dx * I
end

### 保存量 M[u] を計算する．
function M(v)
  M = sum(map(log, v)) # いったん全部足して、
  M = M - 0.5 * ( log(@U(v,0)) + log(@U(v,N)) ) # 台形則なので一番端の重みは半分．
  return Dx * M
end

### exp の差分商式
function dexp(a,b)
  if a != b
    return ( exp(a)-exp(b) )/( a - b )
  else
    return exp(a)
  end
end

### DVDMスキームそのものの式．現在値と次ステップの値をもらって、本来ゼロになるべき量．
function scheme(vp,v)

  f = similar(vp)

  # 本来の方程式+BC の構成は DAE(代数微分方程式)に近い．数値的には DAE は解きにくいことで有名で厄介だ．
  # よって、解くときは方程式に境界条件を繰り込んで、純粋な微分方程式に近い形に直したほうが、数値的には安定して解きやすい．
  # その結果が以下のとおりで、最初と最後の式が境界条件を受けて変形する．
  @U(f,0) = @U(vp,0) - @U(v,0) - 2 * gamma_r * ( dexp( @U(vp,1), @U(v,1) ) - dexp( @U(vp,0), @U(v,0) ) )
  @U(f,N) = @U(vp,N) - @U(v,N) - 2 * gamma_r * ( dexp( @U(vp,N-1), @U(v,N-1) ) - dexp( @U(vp,N), @U(v,N) ) )

  # 残りの式
  for k in 1:N-1
    @U(f,k) = @U(vp,k) - @U(v,k) - gamma_r * ( dexp( @U(vp,k+1), @U(v,k+1) ) - 2 * dexp( @U(vp,k), @U(v,k) ) + dexp( @U(vp,k-1), @U(v,k-1) ))
  end

  return f

end

### Newton 法でスキームの解を求める．Jacobian を求めるのに自動微分を使っている．なんて楽なんだ…
function Newton!(vp::Array{Float64,1}, v::Array{Float64,1})

  local i = 1
  local w = similar(vp)

  func(w) = scheme(w, v)
  # 実際に v のときの Jacobian を計算．実質的にこれは単なる命名であって、実際はあとで遅延評価される．
  j = jacobian(func)

  while true

    # 十分にベクトル f がゼロに近ければ終了
    if sum(abs, func(vp)) < Newton_Criterion
      println("Final Newton loop number: ", i) # 最終的な Newton 反復の回数をみておこう．
      return vp # 本来は返さなくてももとの vector が書き換わらないといけないんだが．
    end

    # Newton 反復．これを教科書通りに 1行でプログラムにできる日が来るとは感動的だなあ．
    vp = vp - j(vp) \ func(vp)
    i += 1

  end

end

### 以下、メイン文
println("Program Started.")

# 時間測定開始!
tic() 

# 現在ステップ、次ステップの近似解の入れ物を用意
u = zeros( N+1 ) # ゼロで埋めた配列．N+1 が本来計算すべき値の個数.
# 初期値代入
for k in 0:N
  @U(u, k) = u0( k*Dx )
  end

up = similar(u)
up = copy(u) # 初期は中身を近くしておく．
up = up + (0.0001 .* randn(N+1)) # が，差分商の微分を考えると全く同じはよろしくないので少しずらす．

# 計算は v = log(u) 相当でやるので, それらを用意する．
lu = log(u)
lup = log(up)

# ファイル open
data_file = open(data_fname, "w")
I_file = open(I_fname, "w")
M_file = open(M_fname, "w")

result_out(u, 0.0, data_file, I_file, M_file)

### 時間発展
for loop = 1:N_time

  # Newton 法で 1step 計算する．
  lup = Newton!(lup, lu)

  # 毎回出力するとデータが多すぎるので、skip_time ステップごとに出力する．
  if mod(loop, skip_time) == 0
    up = exp(lup) # 必要なときだけ u = exp(v) に戻す
    result_out(up, loop*Dt, data_file, I_file, M_file)
    end

  # u と up の中身交換(正確にはポインタを交換してるだけ)
  lu, lup = lup, lu 

end

# ファイル close
close(data_file)
close(I_file)
close(M_file)

# 時間測定終了! 実際に計算してみると、さすがに Euler 法より遅いけど，実は Crank-Nicolson 法とほぼ同じ計算時間だな．
s = toq()
# 計算にかかった時間を報告
println("Program ended.")
println("# elapsed time: ", s, " seconds")

なんとまともに動くんだな，これが． 差分商の定義に場合分けが入っていたりして数値計算にとって嫌な予感がする問題なだけに，ちょっと拍子抜けだ．

というわけで結果を見てみよう． まずは近似解そのもの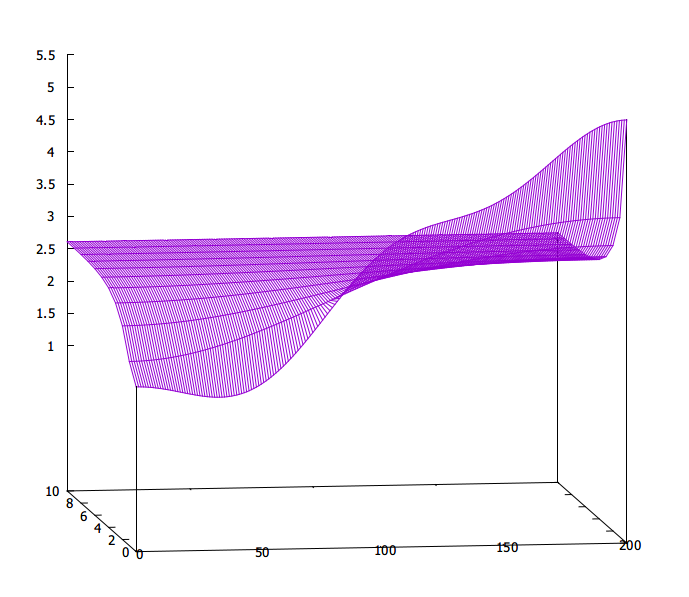． まあ，綺麗に出ますわな． で，次は散逸量 $I_d$ の時間変化をグラフにしてみてみましょ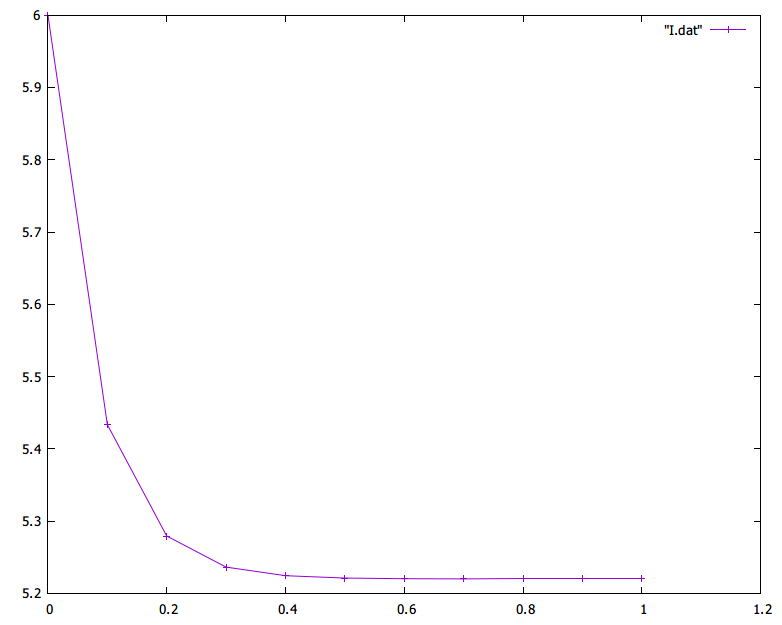． これも綺麗に散逸していますな． でもまあ、ここまでは，他の解法でも同じような結果が出せるので、そう変わらないな．

で，次の保存量の保存性がどれだけくっきり見えるかがポイント． ということで見てみよう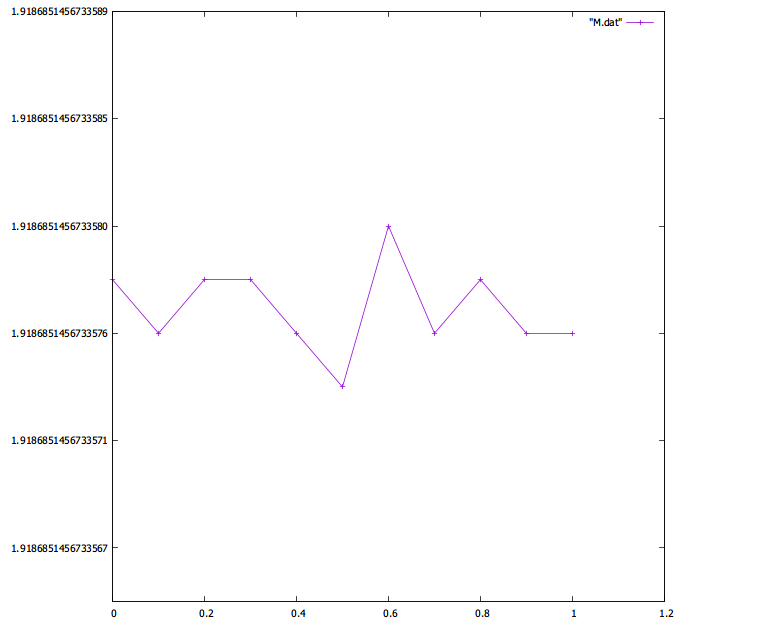． う～む… 正直これはすごい．他の解法といい意味で桁が違うな ¹ ． 倍精度でのマシンイプシロン程度しか揺れとらん． 構造保存ってのはいいねえ…