さて、sample コード: Euler 法 と同じ問題について、Crank-Nicolson スキームを作ってプログラムしてみましょか． CN スキームは、Euler 法の右辺を、「時間ステップが新しいもののみで構成した右辺」と「時間ステップが今のもののみで構成した右辺」の平均に置き換えたもの、と思えばまず間違いない．簡単だな！
では、まず、離散化した関数に相当する $ \u \cong u(k \Dx, n \Dt)$ を用意する．範囲は先のものと同じ $ \Dx = L/N $, $ k = 0,1, \cdots, N $, $ n = 0,1, \cdots . $ でいいな．
次に、境界条件の離散化も同じなんだけど(面倒なので書き写さない)、ちょっとここでひとつ考えておきたいことがある． というのは、そもそも、もともとの問題は 偏微分方程式 + 境界条件 という形式をしてる． で、今回の境界条件であるノイマン境界条件は「境界すぐ近くで、内側の値と外側の値がほぼ同じ」という、離散的には代数的な式に相当することを言っているわけなので、今回の問題は離散的には微分方程式と代数方程式が混じった DAE(代数微分方程式)によく似た構成になってしまっている．
で、非線形な DAE は数値的に解こうとするとかなりたちが悪いことで有名なので、こいつをそのままプログラムに持ち込むことは 大荷物をもって平日朝に千代田線に乗ることと同じぐらい避けたい ．
幸い、今回のような簡単な問題では、境界条件の影響を方程式自身に繰り込んでしまうことが出来るので、そうしよう． こうすると、問題全体が連立微分方程式の形から逸れないので、数値的にはだいぶ安定して解けるはずだ． 実際に境界条件を込めたこの結果は、式で書くと次のような感じ．ん～．
\begin{eqnarray} \frac{\uP -\u}{\Dt} & = & \uP \left( \frac{ u_{k+1}^{(n+1)} - \uP }{\Dx^2} \right) + \u \left( \frac{ u_{k+1}^{(n)} - \u }{\Dx^2} \right), \mbox{ for } k = 0, \newline % \frac{\uP -\u}{\Dt} & = & \frac{1}{2}\left( \uP \dd{k}{2} \uP + \u \dd{k}{2} \u \right), \mbox{ for } k = 1,2,\cdots, N-1, \newline % \frac{\uP -\u}{\Dt} & = & \uP \left( \frac{ u_{k-1}^{(n+1)} - \uP }{\Dx^2} \right) + \u \left( \frac{ u_{k-1}^{(n)} - \u }{\Dx^2} \right), \mbox{ for } k = N. \end{eqnarray}
$ \{ \u \}_{k=0}^{N} $ が既知のときに、上の連立方程式をなんとかして解いて $ \{ \uP \}_{k=0}^{N} $ を求めるのがプログラムの主な仕事になるわけだ．
非線形性はどうするね？
さて、弱いとはいえ上の連立方程式には非線形性があるので、なんとかして解く方法を考えないといけない． 便利なパッケージはいろいろあるのでいくらでも楽をすることはできそうだけど、1 まあ今回は、教科書的に Newton 法を用いて頑張ってみよう．
プログラムで間違えないように、Newton 法のおさらいをしておくぜ． まず、上の連立方程式を左辺から右辺を引いて $\bm{f} (\bm{v}) = \bm{0}$, ただし、$\bm{v} = \left\{ \uP \right\}_{k=0}^N$ と書きなおして、この $\bm{v}$ を求める問題だ、ととらえるわけだな． で、解でない $\bm{v}$ を使うともちろん $\bm{f}(\bm{v}) \neq \bm{0}$ なので、この $\bm{v}$ を $\bm{v} + \bm{\delta v}$ に修正して $\bm{f}(\bm{v} + \bm{\delta v}) \cong \bm{0}$ になるように $\bm{\delta v}$ を計算して、これを修正量として利用すればいい．
幸いこの式を Taylor 展開すれば $\bm{0} \cong \bm{f}(\bm{v}) + J(\bm{v}) \bm{\delta v}$ となるので、 \begin{equation} \bm{\delta v} \cong - J(\bm{v})^{-1} \bm{f}(\bm{v}) \label{eq:newton} \end{equation} として具体的に $\bm{\delta v}$ を計算することが出来、これを所望するだけ繰り返して $\bm{f}(\bm{v}) = \bm{0}$ に近づけるのが Newton 法ということになるな．
この際、 Jacobi行列 $J(\bm{v})$ の計算と, 連立一次方程式を解く操作 $(\ref{eq:newton})$ が必要になるけれども、 Jacobi行列の計算は 自動微分をしてくれる ForwardDiff パッケージ におまかせできるし、 連立一次方程式を解く操作は Julia がもともとその機能を持っているので問題ない． ちなみに、パッケージ ForwardDiff の使い方は 簡単な解説 を書いたんで、そこでも読んでくれ．
やってみるぜ
すると、プログラムは次のような感じになるかな 2 ．
###
using ForwardDiff
### 各種パラメータ
const L = 2.0
const N = 200
const Dx = L/N
const T = 1.0
const Dt = 10.0^(-3)
const N_time = Int(round(T/Dt))
const skip_time = div(N_time,10)
const gamma_r = Dt/(Dx^2)
const data_fname = "data.dat"
const I_fname = "I.dat"
const M_fname = "M.dat"
const Newton_Criterion = 10.0^(-11)
### 注意: 次のマクロについては素人は理解できなくても問題ないので、内容は気にしなくて良い．
### こうすると「素直にプログラムが書けて」「バグが出る可能性を減らせる」だけの話．
###
### Julia 言語での配列の添字は 1 からだが、数式での離散関数の添字は(境界端がゼロなため) 0 からになる．
### このズレに基づくトラブルに悩まされないように、離散関数 u(k) = (プログラム) @U(u,k) = 配列 u[k+1] となるようにマクロ @U を用意する．
### マクロは結果ではなくて式を返すので、この @U(u,k) は実行前に u[k+1] そのものに変換される．つまり、「代入も可能」である!
macro U(v, k)
# Expr(:ref, v, eval( eval(k) + 1 ) ) でもいいが、ちょっとだけ遅いかも(測定できないと思うが). まあ好みの範囲．
Expr(:ref, v, Expr(:call, +, k, 1) )
end
### 初期値を決める関数．境界条件に合っている．
function u0(x)
A0 = 1.0; A1 = 2.0; B2 = 0.3;
A0 + A1 - A1 * cos(pi*x/L) + B2*cos(2*pi*2x/L)
end
### 近似解の値の出力. こういうのは用意しておくと良いねえ．
function result_out(v, time, data_f, I_f, M_f)
println(data_f, "\n## time = $(time)")
for k in 0:N
println(data_f, @U(v,k) )
end
println(I_f, time, " ", I(v) )
println(M_f, time, " ", M(v) )
end
### 散逸量 I[u] を計算する．
function I(v)
I = sum(v) # いったん全部足して、
I = I - 0.5*( @U(v,0) + @U(v,N)) # 台形則なので一番端の重みは半分．
return Dx * I
end
### 保存量 M[u] を計算する．
function M(v)
M = sum(map(log, v)) # いったん全部足して、
M = M - 0.5 * ( log(@U(v,0)) + log(@U(v,N)) ) # 台形則なので一番端の重みは半分．
return Dx * M
end
### Crank-Nicolson スキームそのものの式．現在値と次ステップの値をもらって、本来ゼロになるべき量．
function scheme(vp,v)
f = similar(vp)
# 本来の方程式+BC の構成は DAE(代数微分方程式)に近い．数値的には DAE は解きにくいことで有名で厄介だ．
# よって、解くときは方程式に境界条件を繰り込んで、純粋な微分方程式に近い形に直したほうが、数値的には安定して解きやすい．
# その結果が以下のとおりで、最初と最後の式が境界条件を受けて変形する．
@U(f,0) = @U(vp,0) - gamma_r * @U(vp,0) * ( @U(vp,1) - @U(vp,0) ) - @U(v,0) - gamma_r * @U(v,0) * ( @U(v,1) - @U(v,0) )
@U(f,N) = @U(vp,N) - gamma_r * @U(vp,N) * ( @U(vp,N-1) - @U(vp,N) ) - @U(v,N) - gamma_r * @U(v,N) * ( @U(v,N-1) - @U(v,N) )
# 残りの式
for k in 1:N-1
@U(f,k) = @U(vp,k) - 0.5 * gamma_r * @U(vp,k) * ( @U(vp,k+1) - 2 * @U(vp,k) + @U(vp,k-1) ) - @U(v,k) - 0.5 * gamma_r * @U(v,k) * ( @U(v,k+1) - 2 * @U(v,k) + @U(v,k-1) )
end
return f
end
### Newton 法でスキームの解を求める．Jacobian を求めるのに自動微分を使っている．なんて楽なんだ…
function Newton!(vp::Array{Float64,1}, v::Array{Float64,1})
local i = 1
local w = similar(vp)
func(w) = scheme(w, v)
# 実際に v のときの Jacobian を計算．実質的にこれは単なる命名であって、実際はあとで遅延評価される．
j = jacobian(func)
while true
# 十分にベクトル f がゼロに近ければ終了
if sum(abs, func(vp)) < Newton_Criterion
println("Final Newton loop number: ", i) # 最終的な Newton 反復の回数をみておこう．
return vp # 本来は返さなくてももとの vector が書き換わらないといけないんだが．
end
# Newton 反復．これを教科書通りに 1行でプログラムにできる日が来るとは感動的だなあ．
vp = vp - j(vp) \ func(vp)
i += 1
end
end
### 以下、メイン文
# 時間測定開始!
tic()
# 現在ステップ、次ステップの近似解の入れ物を用意
u = zeros( N+1 ) # ゼロで埋めた配列．N+1 が本来計算すべき値の個数.
# 初期値代入
for k in 0:N
@U(u, k) = u0( k*Dx )
end
up = similar(u)
up = copy(u) # 初期は中身を同じにしておく．
# ファイル open
data_file = open(data_fname, "w")
I_file = open(I_fname, "w")
M_file = open(M_fname, "w")
result_out(u, 0.0, data_file, I_file, M_file)
### 時間発展
for loop = 1:N_time
# 1step 計算する．本当は Newton! 関数の中で up が書き換えられているはずだが、なんかおかしいな．convert のせいか？
up = Newton!(up, u)
# 毎回出力するとデータが多すぎるので、skip_time ステップごとに出力する．
if mod(loop, skip_time) == 0
result_out(up, loop*Dt, data_file, I_file, M_file)
end
# u と up の中身交換(正確にはポインタを交換してるだけ)
u, up = up, u
end
# ファイル close
close(data_file)
close(I_file)
close(M_file)
# 時間測定終了! 実際に計算してみると、さすがに Euler 法よりだいぶ遅いな．
s = toq()
# 計算にかかった時間を報告
println("# elapsed time: ", s, " seconds")
プログラムのポイントは、やっぱり、Jacobi行列を手で計算してその式を入力しているような部分が存在しないで済んでいるところかな． Newton 法が実質的に 1行で書けてしまう のは正直自分でもびっくりだ．
あと、Euler法に比べると $\Dt$ が随分大きく取れることにも注目したい．かなり安定だ な．
で、こいつのファイル名が cn.jl とすると、実行するには
julia cn.jl
とでもすればいい．Euler 法のとき同様に、近似解データと、散逸量 $I_d$, 保存量 $M_d$ の時間経過のデータがファイルに吐き出される．
それぞれ gnuplot でグラフにしてみると、
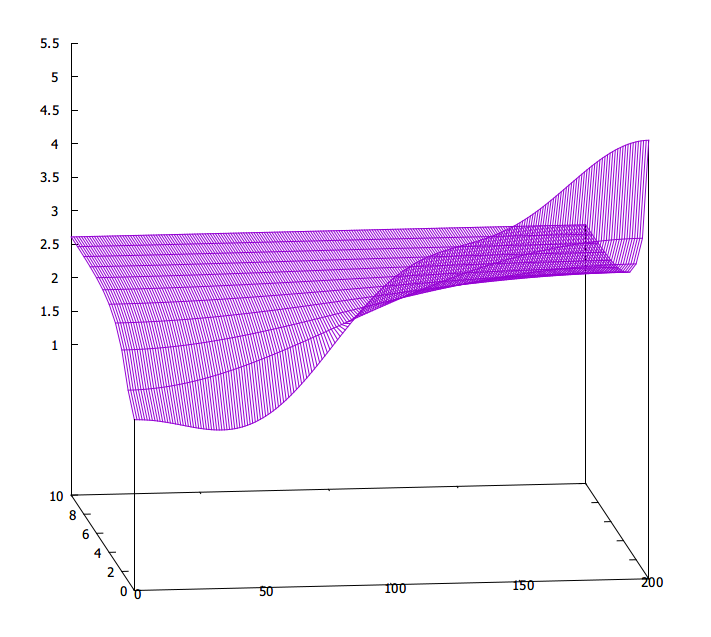が近似解で、
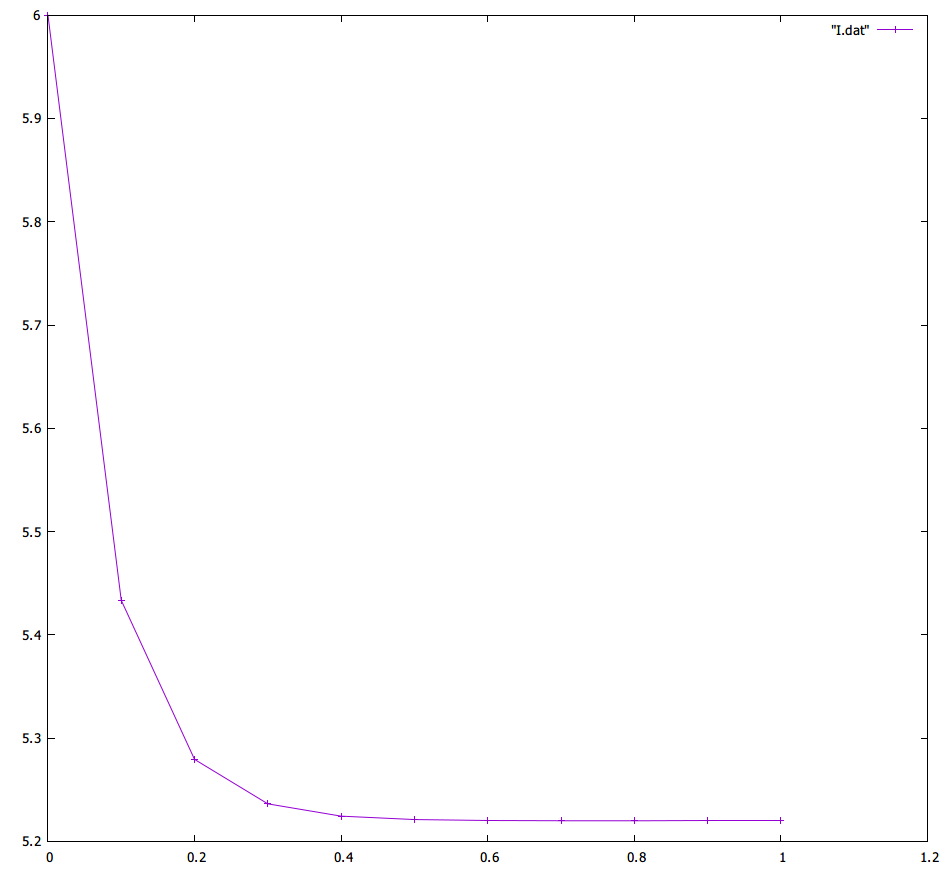が散逸量 $I_d$,
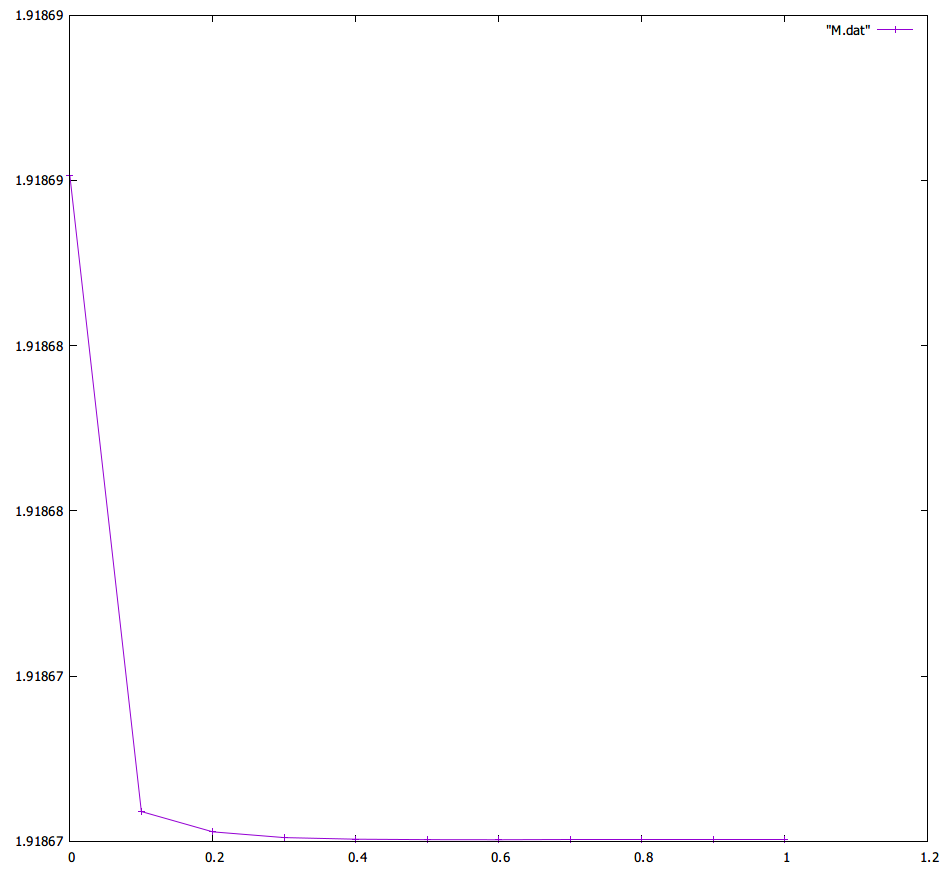が保存量 $M_d$ になる．
ん～、悪くない、いや、まったく実に悪くないねえ．さすがだ．