問題設定
空間変数を $x$, 時間変数を $t$ として、関数 $u(x,t)$ に対する偏微分方程式 \begin{equation} \pdrv{u}{x} = u \pdrv{^2 u}{x^2} \mbox{ } \mbox{ in } \mbox{} \Omega = [0, L] \end{equation} が対象問題.
ただし、境界条件はノイマンゼロ境界条件、すなわち、 \begin{equation} \pdrv{u}{x} = 0 \mbox{ at } x = 0, L \end{equation} としてあって、 初期値は \begin{equation} u(x, 0) = u_0(x) \end{equation} で与える.
また、初期値は正、つまり、 \begin{equation} u_0(x) > 0 \mbox{ for } {}^{\forall} x \mbox{ in } \Omega. \end{equation} である.
このとき、この問題に対する解 $u(x,t)$ の近似解を計算で求めることがわれわれのやりたいこと、になるな.
まあまずは安直な Euler 法でもいかが?
まず、関数を離散化して、 $ \u \cong u(k \Dx, n \Dt)$ としておく. ただし、 $ \Dx = L/N $, $ k = 0,1, \cdots, N $, $ n = 0,1, \cdots . $ だな.
そして、Euler 数値解法は、ごく単純にもとの偏微分方程式を近似した \begin{equation} \frac{\uP - \u}{\Dt} = \u \cdot \dd{k}{2} \left( \u \right) \mbox{ for } k = 0,1, \cdots, N . \end{equation} がまあ妥当かな.ちなみに $\dd{k}{2}$ ってのは普通の二階中心差分作用素だな.
この式の右辺に、$k = 0$ のときに未定義の量 $ u_{-1}^{(n)} $ が、$ k = N $ のときには同様に未定義の $ u_{N+1}^{(n)} $ が登場するが、この二つの量の扱いは境界条件を実現することで決まる.あとできちんと扱うのでそれまで放置.
さて、この式の中で、未知な $ \uP $ を左辺に、既知な $ \u $ を右辺に移項すると、つぎのように書き換えられる.
\begin{equation}
\uP = \u + \frac{\Dt}{\Dx^2} \cdot \u \cdot \left( \ur - 2\u + \ul \right)
\mbox{ for }
k = 0,1, \cdots, N .
\end{equation}
これをもとにプログラムを組む.
そして、境界条件だけど、ノイマン境界条件を離散化したものもごく素直に一階中心差分 $\dd{k}{1}$ を使って
\begin{equation}
\dd{k}{1} \u = 0
\mbox{ at }
k = 0, N.
\end{equation}
とするのがまあ自然だろうな.ちなみにこの境界条件はもっとわかりやすく変形すると、
\begin{equation}
u_{-1}^{(n)} = u_{1}^{(n)},
u_{N+1}^{(n)} = u_{N-1}^{(n)},
\end{equation}
となるので、こっちの方で意識しとくと良さそうだ.
これで先の「未定義な量 2つ」の定義が定まり、安心して問題を解けることになる.
プログラムは、例えば以下の様な感じになるだろう.使っている言語はもちろん Julia である.
ちょっとマクロで工夫したところがあるが、そもそも、もう少しスマートなやり方があるはずだ! というか無かったら泣きたい.
# 各種パラメータ
const L = 2.0
const N = 200
const Dx = L/N
const T = 0.8
const Dt = 10.0^(-5)
const N_time = Int(round(T/Dt))
const skip_M = div(N_time,10)
const gamma = Dt/(Dx^2)
const data_fname = "data.dat"
const I_fname = "I.dat"
const M_fname = "M.dat"
###
### 注意: 次のマクロについては素人は理解できなくても問題ないので、内容は気にしなくて良い.
### こうすると「素直にプログラムが書けて」「バグが出る可能性を減らせる」だけの話.
###
### Julia 言語での配列の添字は 1 からだが、数式での離散関数の添字は(境界の外があるので) -1 からになる.
### このズレに基づくトラブルに悩まされないように、離散関数 u(k) = (プログラム) @U(u,k) = 配列 u[k+2] となるようにマクロ @U を用意する.
### マクロは結果ではなくて式を返すので、この @U(u,k) は実行前に u[k+2] そのものに変換される.つまり、「代入も可能」である!
macro U(u, k)
# Expr(:ref, :u, eval( eval(k) + 2 ) ) でもいいが、ちょっとだけ遅いかも(測定できないと思うが). まあ好みの範囲.
Expr(:ref, :u, Expr(:call, +, k, 2) )
end
### 初期値を決める関数.境界条件に合うようにしておいた.
function u0(x)
A0 = 1.0; A1 = 2.0; B2 = 0.3;
A0 + A1 - A1 * cos(pi*x/L) + B2*cos(2*pi*2x/L)
end
### ノイマン境界条件を満たすように境界の「外」の解の値を設定する. 配列 v をもらって、一番外側の値を修正する.
function BC!(v)
@U(v, -1) = @U(v, 1)
@U(v, N+1) = @U(v, N-1)
return nothing
end
### 近似解の値の出力. こういうのは用意しておくと良いねえ.
function result_out(u, time, data_f, I_f, M_f)
println(data_f, "\n## time = $(time)")
for k in 0:N
println(data_f, @U(u,k) )
end
println(I_f, time, " ", I(u) )
println(M_f, time, " ", M(u) )
end
### 散逸量 I[u] を計算する.
function I(u)
I = sum(u) # いったん全部足して、
I = I - ( @U(u,-1) + @U(u,N+1) ) # 外側の値は境界条件用のダミーなので削除、
I = I - 0.5*( @U(u,0) + @U(u,N)) # 台形則なので一番端の重みは半分.
return Dx * I
end
### 保存量 M[u] を計算する.
function M(u)
M = sum(map(log, u)) # いったん全部足して、
M = M - ( log(@U(u,-1)) + log(@U(u,N+1)) ) # 外側の値は境界条件用のダミーなので削除、
M = M - 0.5 * ( log(@U(u,0)) + log(@U(u,N)) ) # 台形則なので一番端の重みは半分.
return Dx * M
end
### 時間ステップを一つ進める計算 u -> up
function nextstep!(up:: Array{Float64,1}, u:: Array{Float64,1})
# function nextstep!(up, u) でも十分動く.上のように型を宣言しておくと動作が早い、というだけの話.
# 高速なコードにしたければ, 下の計算部分を次のものに取り替える.
# v_m = u[1]
# v = u[2]
# for k in 0:N
# v_p = @U(u, k+1)
# @U(up, k) = v + gamma * v *( v_m - 2v + v_p )
# v_m, v = v, v_p
# end
for k in 0:N
v_m = @U(u, k-1)
v = @U(u ,k)
v_p = @U(u, k+1)
@U(up, k) = v + gamma * v *( v_m - 2v + v_p )
end
BC!(up) # 境界条件処理をする.これを忘れると、次のステップから値がおかしくなる.
end
### 以下、メイン文
# 時間測定開始!
tic()
# 現在ステップ、次ステップの近似解の入れ物を用意
u = zeros( N+1 +2 ) # ゼロで埋めた配列.N+1 が本来計算すべき値の個数で、+2 は境界外部の、境界条件を満たすための偽の値が二つあるため.
up = zeros( length(u) ) # 同じ長さの、ゼロで埋めた配列.
# 初期値代入
for k in 0:N
@U(u, k) = u0( k*Dx )
end
BC!(u)
# ファイル open
data_file = open(data_fname, "w")
I_file = open(I_fname, "w")
M_file = open(M_fname, "w")
result_out(u, 0.0, data_file, I_file, M_file)
### 時間発展
for loop = 1:N_time
# Euler 法で 1step 計算する.
nextstep!(up,u)
# 毎回出力するとデータが多すぎるので、skip_M ステップごとに出力する.
if mod(loop, skip_M) == 0
result_out(up, loop*Dt, data_file, I_file, M_file)
end
# u と up の中身交換(正確にはポインタを交換してるだけ)
u, up = up, u
end
# 時間測定終了!
s = toq()
# 計算にかかった時間を報告
println("# elapsed time: ", s, " seconds")
# ファイル close
close(data_file)
close(I_file)
close(M_file)
これを julia を呼べる環境でシェルから
julia euler_simple.jl
として実行すると、 計算結果そのものが data.dat というファイルに、 散逸量 $ I[u] = \int u \dx$ を離散化した量の時間経過が I.dat というファイルに、 保存量 $ M[u] = \int \log(u) \dx$ を離散化した量の時間経過が M.dat というファイルに出力される.
詳細はともかく、プログラムを読んでみて、時間ステップ幅 $ \Delta t $ が非常にちいさくとってあることには注意すべし. 実際にこれらのパラメータを変えて動かしてみるとわかるが、時間ステップ幅 $ \Delta t $ が大きいと計算結果がふっとんでしまって、計算が続けられない. つまり、 Euler 法は不安定になりやすい のである.
ちなみに、これらの積分量の離散化は素直に台形則を使って \begin{equation} I_d[u] \mbox{ } \defeq \mbox{ } {\sum_{k=0}^N}” u_k \Dx, M_d[u] \mbox{ } \defeq \mbox{ } {\sum_{k=0}^N}” \log(u_k) \Dx \end{equation} としている.
そして、計算結果を gnuplot で splot すると
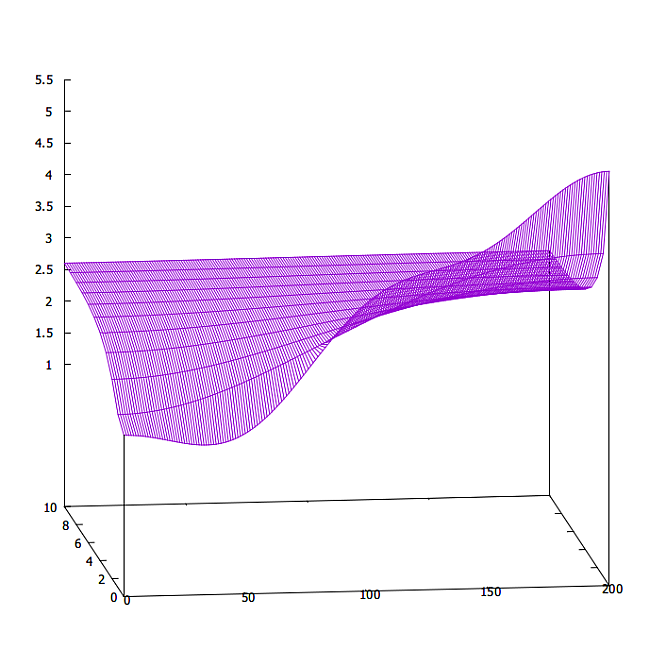 という感じになる.
手前が初期値で、奥へ向かって時間発展している.だんだんなめらかになっているのがよくわかる.
という感じになる.
手前が初期値で、奥へ向かって時間発展している.だんだんなめらかになっているのがよくわかる.
散逸量 $I_d$ の時間変化をグラフにしてみると
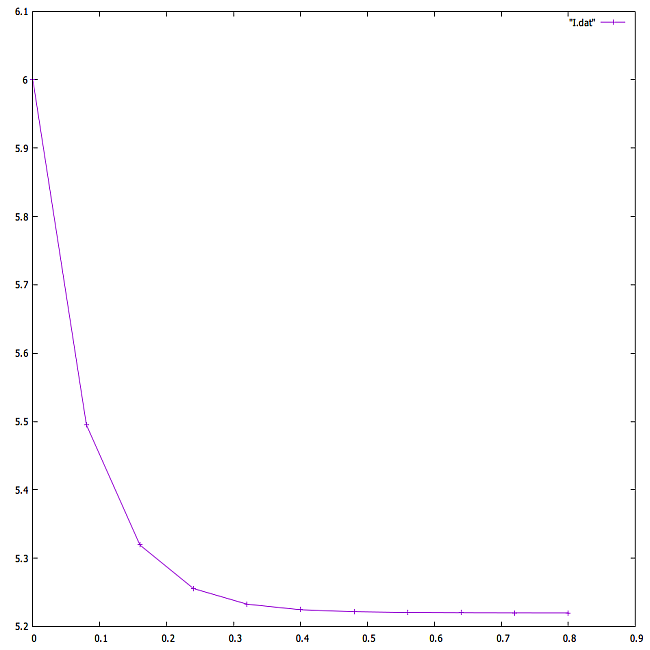 という感じで、まあ確かに散逸しているんだけど、Euler 法だからなあ、あんまり信用出来ないなあ、ということで保存量もチェックしてみる.
保存量 $M_d$ の時間変化をグラフにしてみると、
という感じで、まあ確かに散逸しているんだけど、Euler 法だからなあ、あんまり信用出来ないなあ、ということで保存量もチェックしてみる.
保存量 $M_d$ の時間変化をグラフにしてみると、
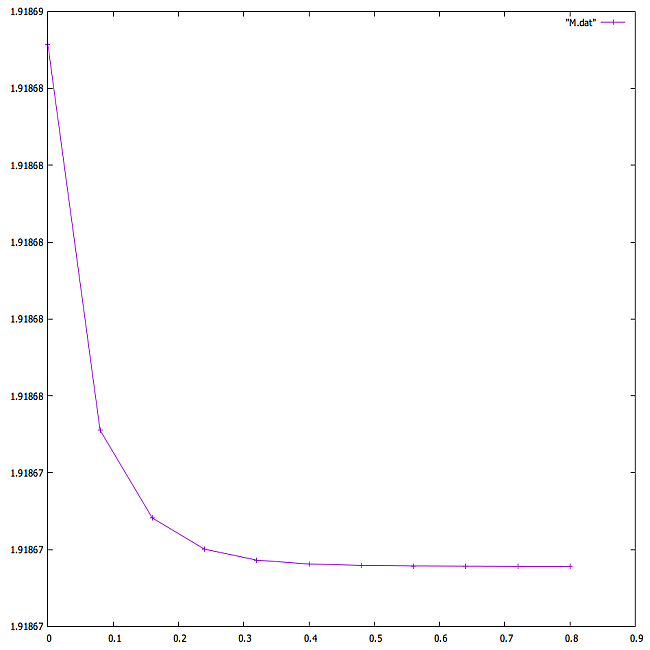 という感じで、おやまあ、わるくないかな.
グラフだけだと結構変化が大きいように見えるけど 1 、縦軸の数字を読むと、これはほぼ保存していると言って良さそうだ.
あとは、$\Dt$ をこんなに小さくとらなくても安定して計算可能ならば嬉しいんだがなあ.
という感じで、おやまあ、わるくないかな.
グラフだけだと結構変化が大きいように見えるけど 1 、縦軸の数字を読むと、これはほぼ保存していると言って良さそうだ.
あとは、$\Dt$ をこんなに小さくとらなくても安定して計算可能ならば嬉しいんだがなあ.
- 最初プログラムにバグが有って、5% 程度減ってるようにみえたときは やっぱり Euler 法はあんまり信用出来ないなあ、なんて思ったりした.ごめん. [return]