数値解析のための個々の話をつなげるために、ここで一つ、Julia を使って、「通しで」いろいろやってみよう. 対象は、ごく簡単なものだけれども、
- 非線形
- 連立
な常微分方程式を扱ってみよう.
Volterra モデル
これは、被食者数を $u(t)$ で、捕食者数を $v(t)$ で表すとして、 以下のような非線形の常微分微分方程式で表されるモデル方程式で、WW-I 時代の実測データを解釈するために作り出された、由緒正しいモデルと言える.
\begin{equation} \left\{\begin{array}{rcl} \displaystyle \frac{du}{dt} & = & - C_1 uv + D_1 u, \cr \displaystyle \frac{dv}{dt} & = & C_2 uv - D_2 v \end{array}\right. \end{equation}
ただし、係数 $C_1$, $C_2$, $D_1$, $D_2$ は全て定数で正としておこう.
相図等についてはあとでチェックするとして、まずはこいつに従って計算してみよう.
まあまずは簡単な Euler 法で
離散時間の近似解を $u_n \cong u(n\Delta t)$, $v_n \cong v(n\Delta t)$, と書くとして、Euler スキームは次のようになるだろう.
\begin{equation} \left\{\begin{array}{rcl} \displaystyle \frac{ u_{n+1} - u_n}{\Delta t} & = & - C_1 u_n v_n + D_1 u_n , \cr \displaystyle \frac{ v_{n+1} - v_n}{\Delta t} & = & C_2 u_n v_n - D_2 v_n \end{array}\right. \end{equation}
これを分かりやすく書き直すと次のようになる.
\begin{equation} \left\{\begin{array}{rcl} u_{n+1} & = & u_n - \Delta t C_1 u_n v_n + \Delta t D_1 u_n = (1 + \Delta t D_1 - \Delta t C_1 v_n ) u_n, \cr % v_{n+1} & = & v_n + \Delta t C_2 u_n v_n - \Delta t D_2 v_n = (1 - \Delta t D_2 + \Delta t C_2 u_n ) v_n \end{array}\right. \end{equation}
定数などを、 $C_1 = $ $C_2 = $ $D_1 = $ $D_2 = 1.0$, $u(0) = v(0) = 0.7$, $\Delta t = 0.05$ としてやってみよう.
まず定数を設定して、そのあとにスキームを関数として定義しよう.
C1 = C2 = D1 = D2 = 1.0 # こういう記法が許されるのが、Julia の地味にいいところ.
u0 = v0 = 0.7
Δt = 0.05
function euler(u,v)
u_new = (1 + Δt*D1 - Δt*C1*v) * u
v_new = (1 - Δt*D2 + Δt*C2*u) * v
u,v = u_new, v_new
return u, v
end
初期値を試しに入れて、動作するかどうか確かめてみよう
euler(u0,v0)
(0.7105,0.6895)
うまくいきそうなので,思い切って 500ステップほど動かしてみようか.
u,v = u0, v0
uv_sq = [ u0, v0 ]
for i in 1:500
u,v = euler(u,v) # これで時間発展させて、
uv_sq = hcat(uv_sq, [u,v]) # あとでグラフを描くために、データを配列に追加して録っておく
end
結果をまずちょっと眺めてみて、
uv_sq
2×501 Array{Float64,2}:
0.7 0.7105 0.721531 0.733092 0.745186 … 0.353772 0.353133 0.353086
0.7 0.6895 0.679519 0.670058 0.661116 1.03614 1.00266 0.970234
グラフにしてみよう
using Plots
gr() # Plots/gr を使う準備をして…
plot(uv_sq')
# 行列を与えると、縦ベクトルを別々のグラフとして描いてくれる.ちなみに,' で行列を転置している.
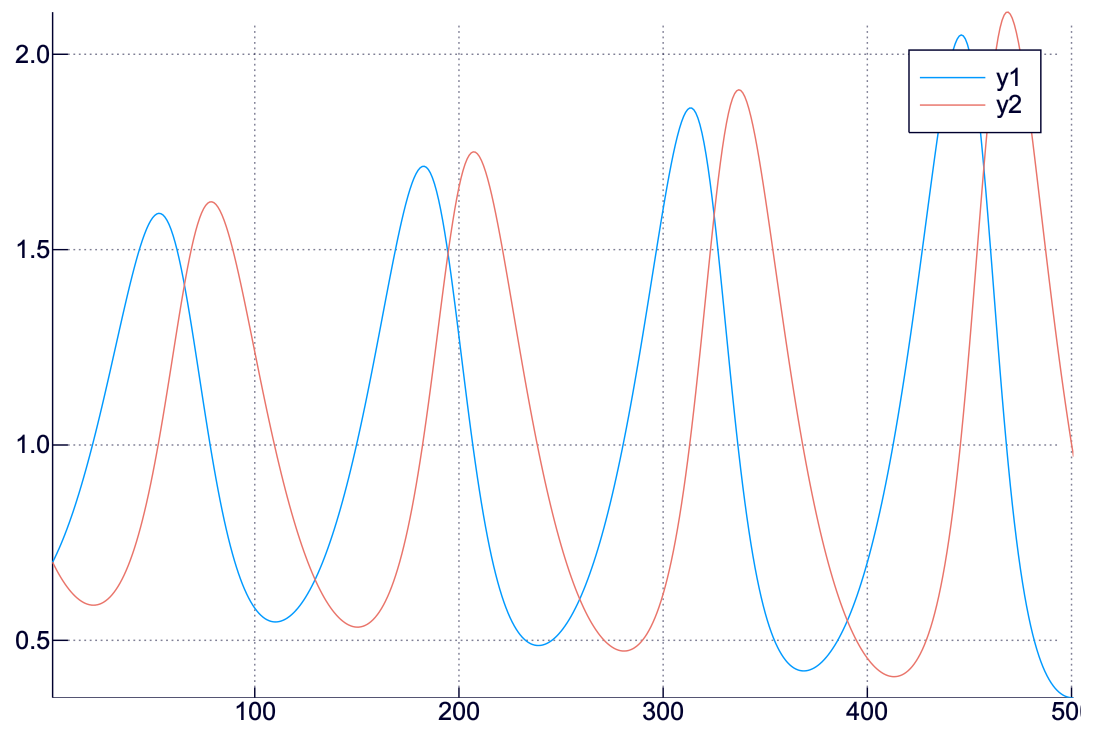 青線が $u_n$ で、赤線が $v_n$ だね.
青線が $u_n$ で、赤線が $v_n$ だね.
横軸が $t$ にあっていないとわかりにくいので、ちゃんとしてみよう.
t_sq = [0:Δt:500*Δt]
plot(t_sq, uv_sq')
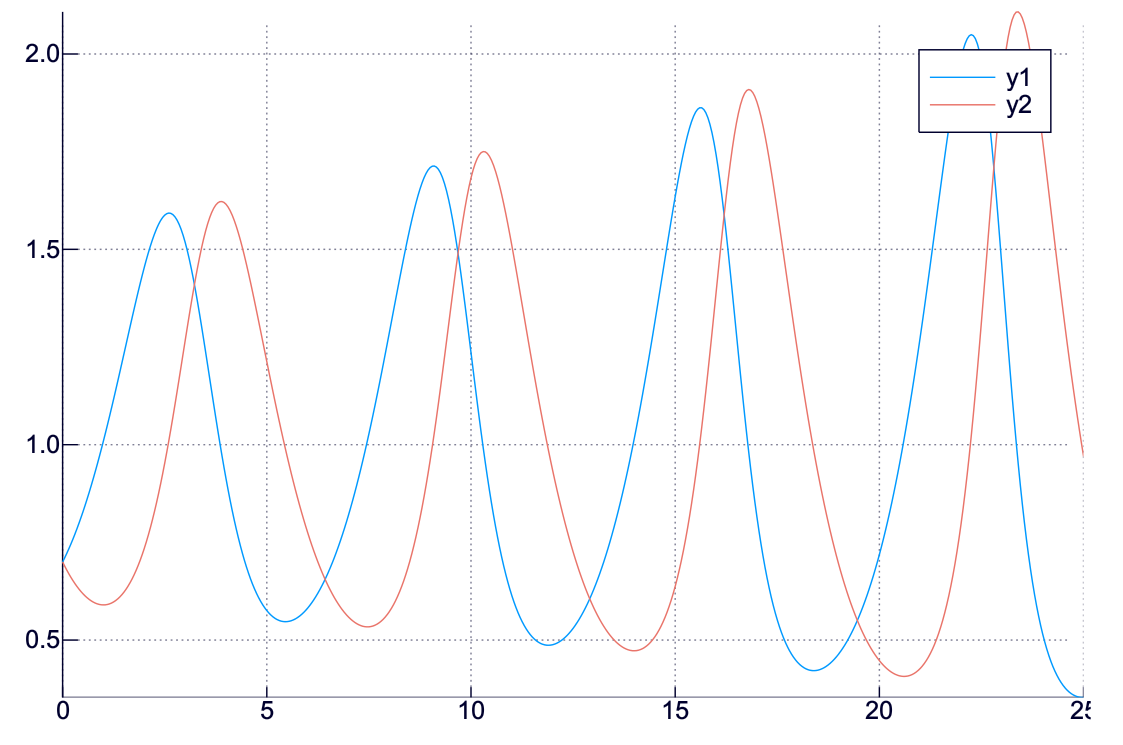 ふ〜む、だんだん振幅が大きくなっているけど本当かな?
ちょっと $\Delta t$ を小さくしてみて、変化したりしないかチェックしてみよう.
ふ〜む、だんだん振幅が大きくなっているけど本当かな?
ちょっと $\Delta t$ を小さくしてみて、変化したりしないかチェックしてみよう.
上のグラフと比べるには、同じ時間($t=25.0$)まで計算すればいいだろうから、そういう風に変更しよう.
Δt = 0.01
lastT = 25
N = Int(lastT/Δt)
u,v = u0, v0
uv_sq = [ u0, v0 ]
for i in 1:N
u,v = euler(u,v)
uv_sq = hcat(uv_sq, [u,v])
end
t_sq = 0:Δt:lastT
plot(t_sq, uv_sq')
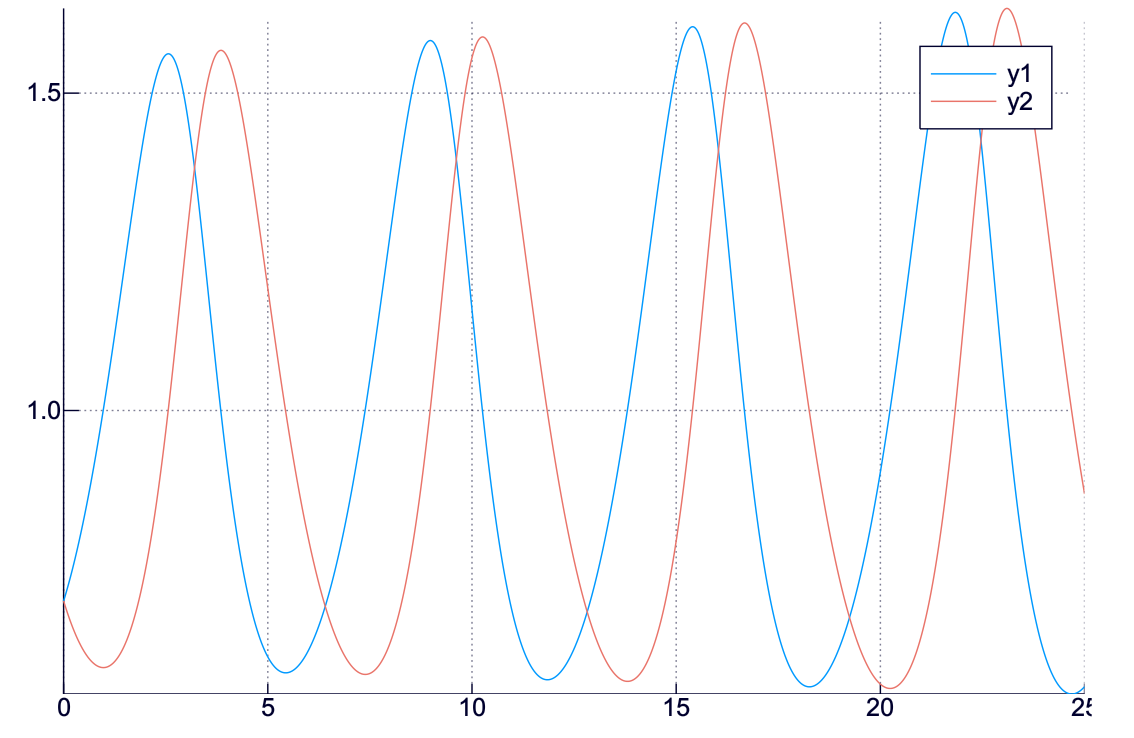 んん? 随分変わったぞ? 振幅が余り変わらなくなった.どうやら Euler スキームはこの問題だと少し信用ならないようだな.もう少し信用できそうな方法で計算し直そう.
んん? 随分変わったぞ? 振幅が余り変わらなくなった.どうやら Euler スキームはこの問題だと少し信用ならないようだな.もう少し信用できそうな方法で計算し直そう.
時間方向に対称なスキームを作って動かしてみる
Euler スキームは信用ならないようなので、もう少しまともなスキームを作ってみよう. いろんな考え方があるが、まあ、まずは時間方向に対称なスキームを作るのが、手がかりのないときのセオリーかな.
対称なスキームと言っても作り方は無数にバリエーションが有るが、ここでは単純に次のようなものを考えてみよう.
\begin{equation} \left\{\begin{array}{rcl} \displaystyle \frac{ u_{n+1} - u_n}{\Delta t} & = & \displaystyle - C_1 \left( \frac{ u_{n+1} v_{n+1} + u_n v_n }{2} \right) + D_1 \left( \frac{ u_{n+1} + u_n }{2} \right), \cr \displaystyle \frac{ v_{n+1} - v_n}{\Delta t} & = & \displaystyle C_2 \left( \frac{ u_{n+1} v_{n+1} + u_n v_n }{2} \right) - D_2 \left( \frac{v_{n+1} + v_n}{2} \right) \end{array}\right. \end{equation}
これは次のように書き直せるので、 \begin{equation} \left\{\begin{array}{rcl} 0 & = & \displaystyle \left( 1 + \frac{\Delta t}{2} \left( - D_1 + C_1 v_{n+1} \right) \right) u_{n+1} + \left( -1 + \frac{\Delta t}{2} \left( - D_1 + C_1 v_{n} \right) \right) u_{n} , \cr 0 & = & \displaystyle \left( 1 + \frac{\Delta t}{2} \left( D_2 - C_2 u_{n+1} \right) \right) v_{n+1} + \left( -1 + \frac{\Delta t}{2} \left( D_2 - C_2 u_{n} \right) \right) v_{n} \end{array}\right. \end{equation} $u_n, v_n$ を既知として、この連立非線形方程式を解いて $u_{n+1}, v_{n+1}$ を求めれば時間ステップを一つ進めることが出来る.
それには、NLsolve パッケージの nlsolve() を使えば良いので、次のような感じになるだろう.
まずパッケージの使用宣言をして、
using NLsolve
それから、0 になって欲しい(連立)方程式を以下のように定義しておいて、
function symm(u_new, u_curr)
up, vp, u, v = u_new[1], u_new[2], u_curr[1], u_curr[2]
half = Δt/2
r = similar(u_new)
r[1] = ( 1 + half * ( - D1 + C1*vp ) )*up + ( -1 + half * ( -D1 + C1*v ) )*u
r[2] = ( 1 + half * ( D2 - C2*up ) )*vp + ( -1 + half * ( D2 - C2*u ) )*v
return r
end
これを満たす近似解を求めるようにスキームを関数として定義する.このあたりのご託宣は NLsolve: 非線形方程式の求根 package に説明してあるので読むといいだろう.
function symmetric(u_curr)
u_new = nlsolve( (vin,vout)->vout.=symm(vin,u_curr), u_curr, autodiff=true ).zero
return u_new
end
初期値を試しに入れて、動作するかどうか確かめてみよう.
symmetric([u0, v0])
2-element Array{Float64,1}:
0.710763
0.689762
うん、Euler スキームの解とほぼ同じで、おかしくはなさそうだ.
よって、これも同様に 500ステップほどすすめてみよう.
u = [ u0, v0 ] # 現在値を u としよう.最初はもちろん初期値だ.
u_sq = copy(u) # これはデータ記録用の配列.
for i in 1:500
u = symmetric(u) # スキームによって時間発展.
u_sq = hcat(u_sq, u) # 配列に追加していく.
end
結果の数字を眺めてみよう.
u_sq
2×501 Array{Float64,2}:
0.7 0.710763 0.722051 0.733865 0.746205 … 0.603713 0.606901 0.610638
0.7 0.689762 0.680049 0.67086 0.662195 0.903499 0.885843 0.868681
変では無さそうだ.ではグラフを描いてみよう.
plot(u_sq')
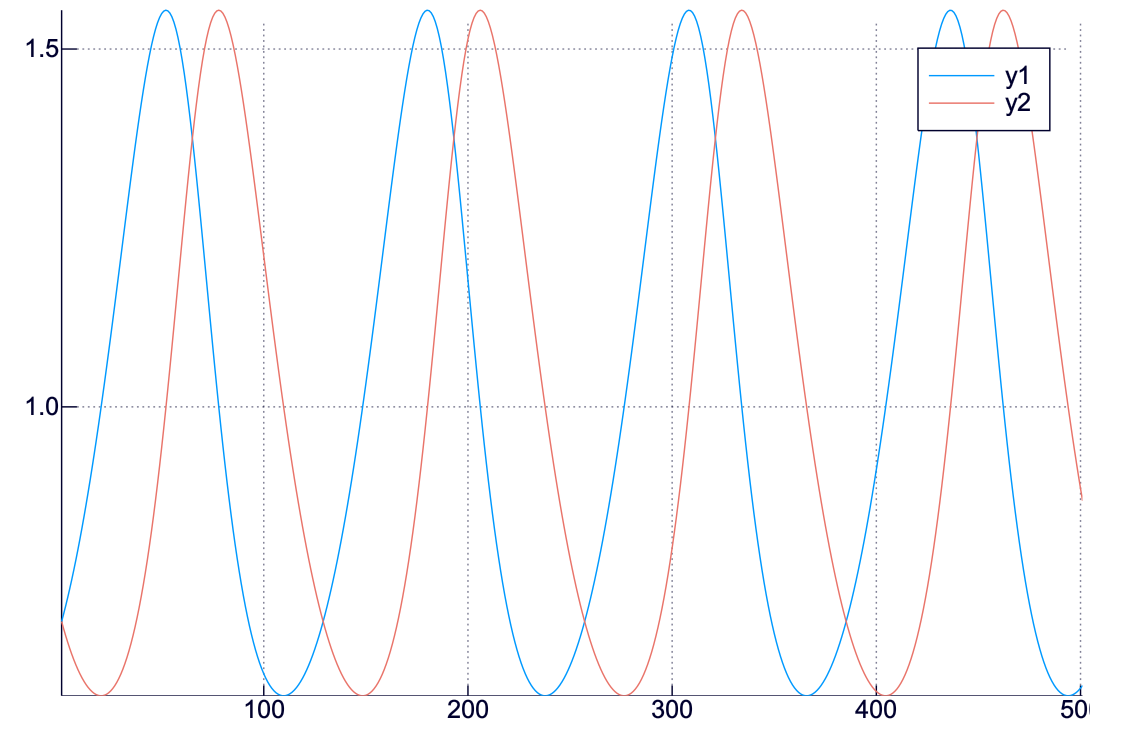 おお! 大変きれいに振幅が揃っている! おそらく、これはかなり「良い近似解」であると期待してよいのではないだろうか? そんな雰囲気が漂ってくるというものだ.
おお! 大変きれいに振幅が揃っている! おそらく、これはかなり「良い近似解」であると期待してよいのではないだろうか? そんな雰囲気が漂ってくるというものだ.
相図をみてみよう
結果がそこそこまっとうそうなので、この結果を相図にして、様子を見てみよう.なにか見えてくるものがあるかもしれない.
us, vs = u_sq[1,:], u_sq[2,:]
plot(us, vs, aspect_ratio = 1)
# aspect_ratio は、縦横の軸目盛りの比率の指定.1 にすると、縦横の縮尺が一致する.
plot!((u0,v0), marker = :circle, lab = "initial value")
# lab に指定した文字列は、legend に現れる
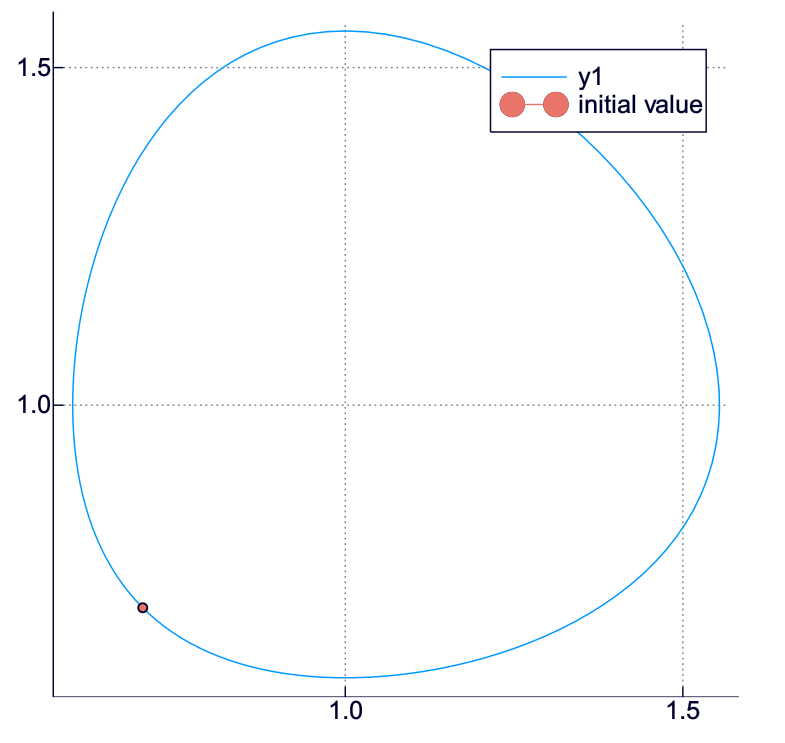 うん、この相図からは、系がきれいに「元へ戻ってくる」ことがみてとれる.
うん、この相図からは、系がきれいに「元へ戻ってくる」ことがみてとれる.
漁業の影響を見てみよう
漁業の影響がどう出るか、Volterra モデルで見てみよう. これがこのモデルの「キモ」であるので、注意深く考えながらやろう.
まず、モデルの数式は、漁業の影響係数 $E > 0$ を用いて、次のようになる.
$\left\{\begin{array}{rcl} \displaystyle \frac{du}{dt} & = & - C_1 uv + D_1 u - E u, \cr \displaystyle \frac{dv}{dt} & = & C_2 uv - D_2 v - E v \end{array}\right.$
そこで、この係数 $E$ を $E = 0.5$ として以下、計算してみよう.
$E$ があることによる影響は、$D_1, D_2$ の変化と同じなので、漁業影響ありのスキームは簡単に以下のように作ることが出来る.
E = 0.5
function symm_fishing(u_new, u_curr, E)
up, vp, u, v = u_new[1], u_new[2], u_curr[1], u_curr[2]
half = Δt/2
r = similar(u_new)
r[1] = ( 1 + half * ( - D1 + E + C1*vp ) ) * up + ( -1 + half * ( -D1 + E + C1*v ) ) * u
r[2] = ( 1 + half * ( D2 + E - C2*up ) ) * vp + ( -1 + half * ( D2 + E - C2*u ) ) * v
return r
end
function symmetric_fishing(u_curr, E)
u_new = nlsolve( (vin,vout)->vout.=symm_fishing(vin,u_curr,E), u_curr, autodiff=true ).zero
return u_new
end
初期値を入れて、挙動を見てみよう.
symmetric_fishing([u0, v0], E)
2-element Array{Float64,1}:
0.69351
0.672442
うん、変では無さそうだ.では早速、これも 500ステップすすめてみよう.
u = [ u0, v0 ] # 現在値を u としよう.最初はもちろん初期値だ.
uf_sq = copy(u) # これはデータ記録用の配列.
for i in 1:500
u = symmetric_fishing(u, E) # スキームによって時間発展.
uf_sq = hcat(uf_sq, u) # 配列に追加していく.
end
結果を覗いてみると、
uf_sq
2×501 Array{Float64,2}:
0.7 0.69351 0.688013 0.683455 0.679788 … 0.762046 0.771829 0.78208
0.7 0.672442 0.645775 0.620009 0.595149 0.249395 0.240418 0.231879
ふむ、変なことは起きていなさそうな気配だ.では、グラフを見てみよう.
plot(uf_sq')
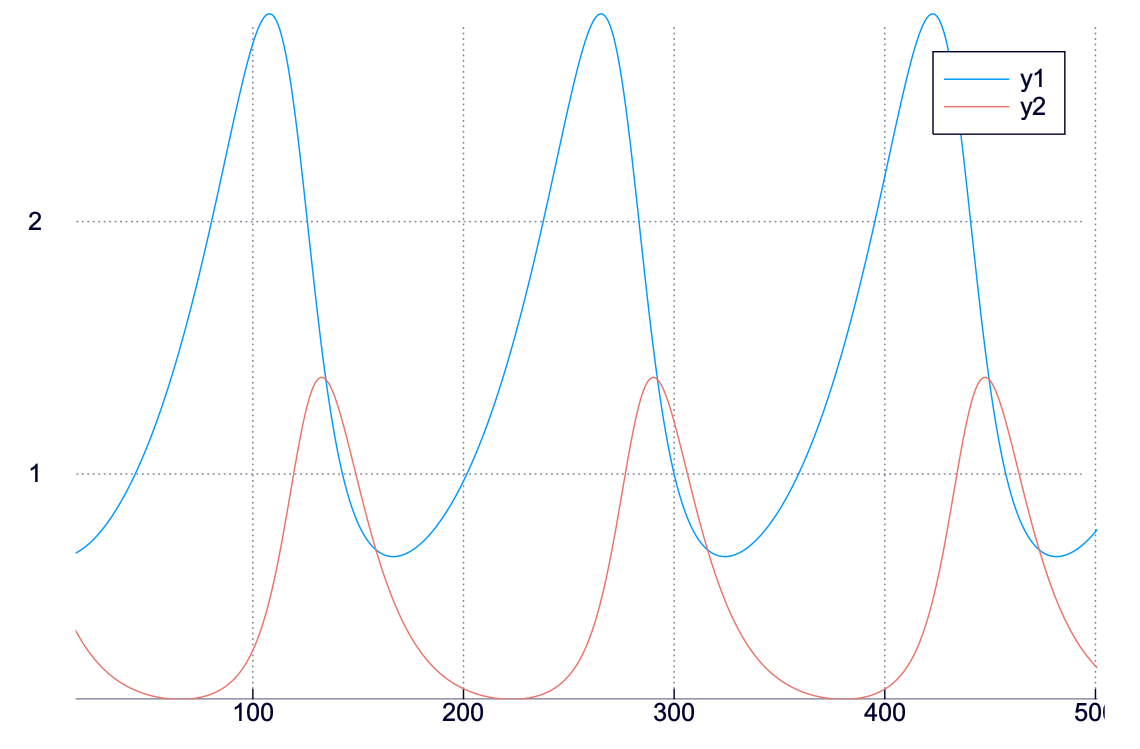 んんん? これは随分変わったな.早速相図を描いてみよう.
んんん? これは随分変わったな.早速相図を描いてみよう.
ufs = uf_sq[1,:]
vfs = uf_sq[2,:]
plot(ufs, vfs, aspect_ratio = 1)
plot!((u0,v0), marker = :circle, lab = "initial value")
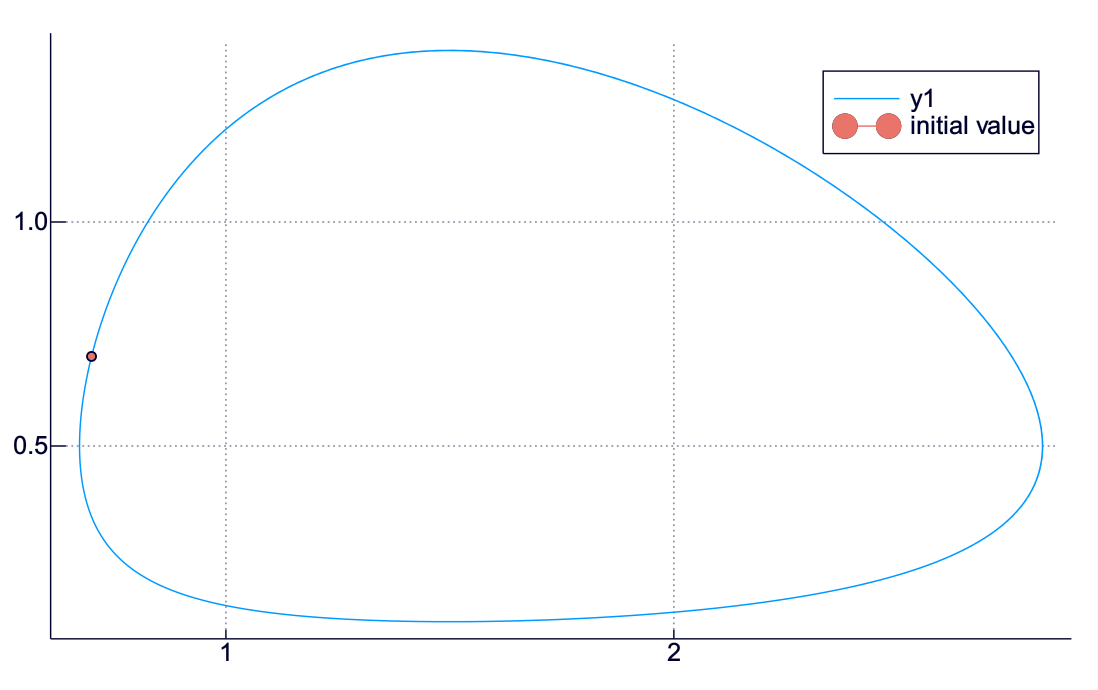 やはり系は「元へ戻ってくる」保存系のようだ.
やはり系は「元へ戻ってくる」保存系のようだ.
漁業による影響変化を見たいので、漁業効果の入っていないデータと一緒に描いてみよう.
plot(us, vs, aspect_ratio = 1)
plot!(ufs, vfs)
plot!((u0,v0), marker = :circle, lab = "initial value")
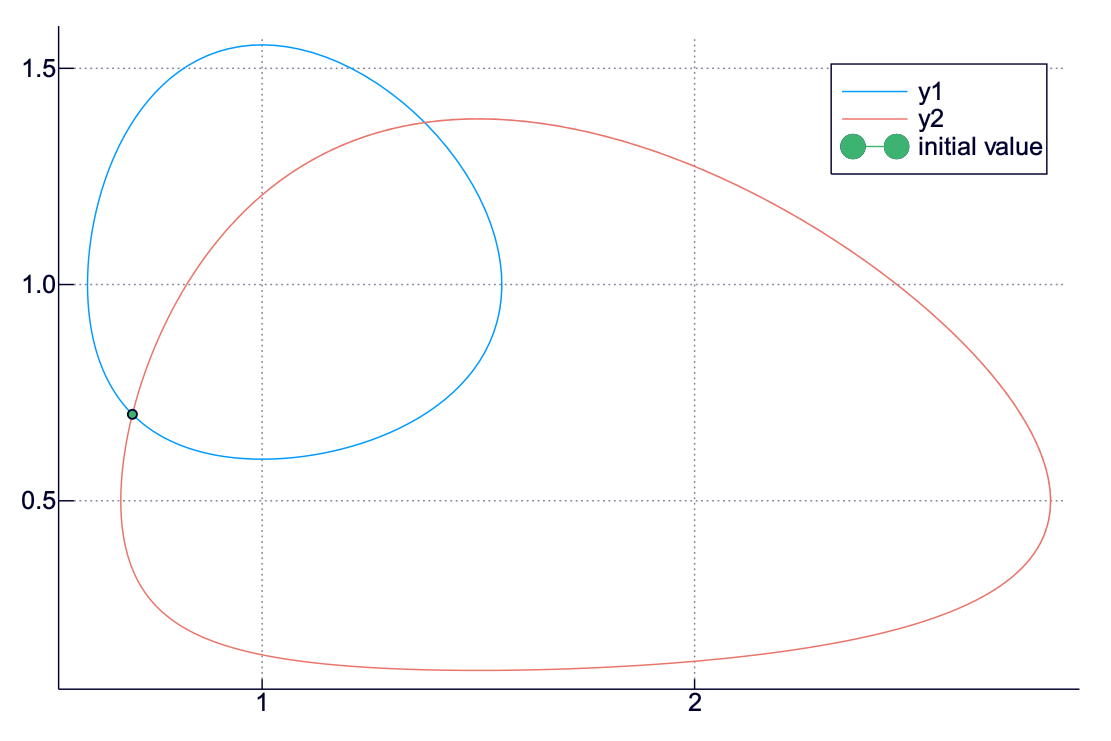
どうやら、漁業が行われると、相図の上での軌跡の中心相当の点が右下にずれるようだ.
じつはこの「軌跡の中心相当の点」は幸いにも手計算で求めることが出来て、
漁業なし… 中心 $\displaystyle = \left(\frac{D_2}{C_2}, \frac{D_1}{C_1}\right)$,
漁業あり… 中心 $\displaystyle = \left(\frac{D_2 + E}{C_2}, \frac{D_1 - E}{C_1}\right)$
ということがわかっている.そこでこれも相図に描き込んでみよう.
plot(us, vs, aspect_ratio = 1)
plot!(ufs, vfs)
plot!((u0,v0), marker = :circle, lab = "initial value")
plot!((D2/C2,D1/C1), marker = :circle, lab = "center without fishing")
plot!(((D2 + E)/C2,(D1 - E)/C1), marker = :circle, lab = "center with fishing")
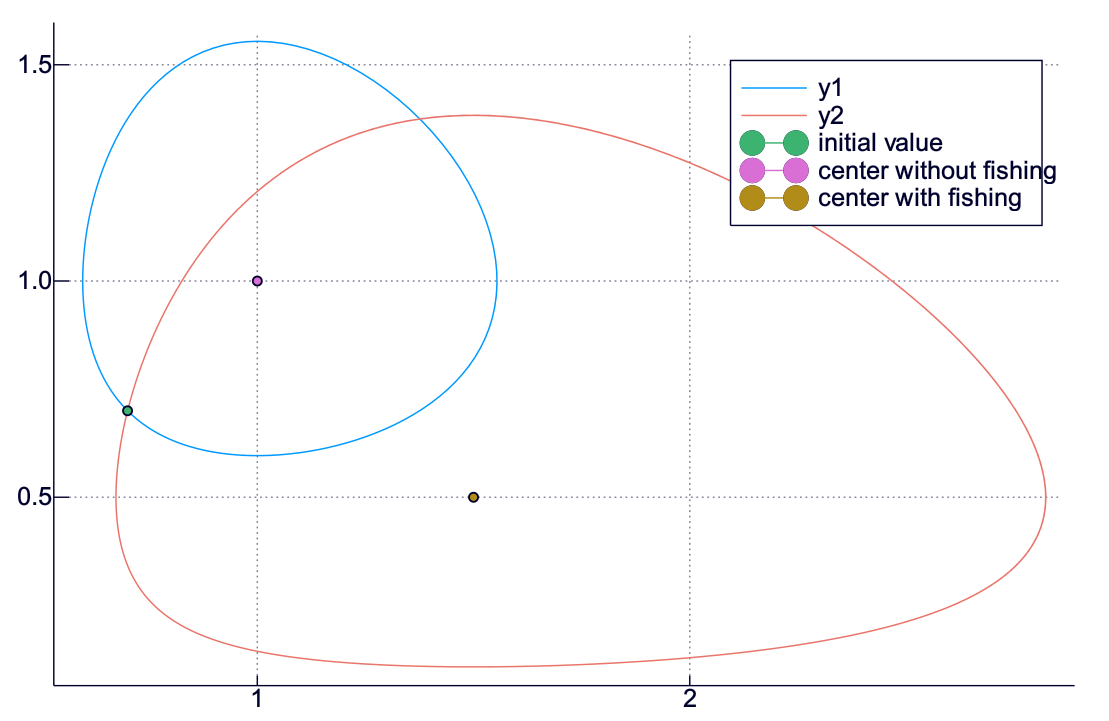 なんとなく、いろいろと分かってきたようなきがするのではないだろうか.
なんとなく、いろいろと分かってきたようなきがするのではないだろうか.
漁業の影響の大きさをいろいろ変えてみてみよう
リアルタイムでパラメータ変化による影響を見ることが出来る, Interact パッケージを使えば良いわけだ. Interact パッケージについては、 Interact: GUI を使って計算パラメータをリアルタイムで変化させる package に解説を書いたので、そこを参照して欲しい.
まずパッケージの使用宣言をして、
using Interact
あとは、普通に、「$E$ が変わったらやり直したいこと」を @manipulate for ... end の中に書くだけだ.
@manipulate for E in 0.0:0.01:0.99
u = [ u0, v0 ] # 現在値を u としよう.最初はもちろん初期値だ.
uf_sq = copy(u) # これはデータ記録用の配列.
for i in 1:500
u = symmetric_fishing(u, E) # スキームによって時間発展.
uf_sq = hcat(uf_sq, u) # 配列に追加していく.
end
ufs = uf_sq[1,:]
vfs = uf_sq[2,:]
plot(us, vs, aspect_ratio = 1)
plot!(ufs, vfs)
plot!((u0,v0), marker = :circle, lab = "initial value")
plot!((D2/C2,D1/C1), marker = :circle, lab = "center without fishing")
plot!(((D2 + E)/C2,(D1 - E)/C1), marker = :circle, lab = "center with fishing")
end
すると、下図のように、$E$ をマウスで変更できるスライダーと共に図が描かれ、リアルタイムで変化が見られる.
もちろん、スムースさはコンピュータの計算速度に依存するが…
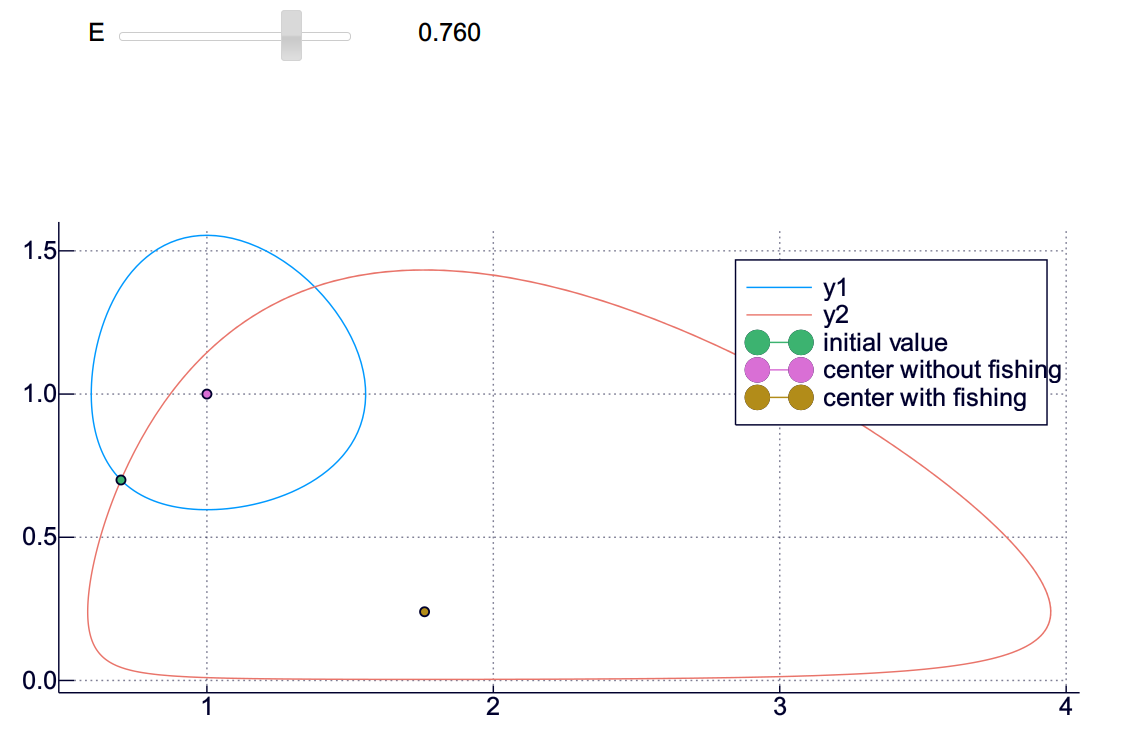
どうだろう、ごく簡単な問題について、ごく簡単な作業をやってみたが、数値解析に Julia を使う感覚が少しわかってきたのではないだろうか.