¼ø¶È»ñÎÁ/12
´Ø¿ô¤ÎËâË¡: ºÆµ¢ÄêµÁ †
¸½Âå¤Î¥³¥ó¥Ô¥å¡¼¥¿¤Î¹âµé¸À¸ì¤Î´Ø¿ô¤Ç¤Ï¡¤¼«Ê¬¼«¿È¤òÄêµÁ¤Ë»È¤¦¡ÖºÆµ¢ÄêµÁ¡×¤È¤¤¤¦ËâË¡¤¬»È¤¨¤ë¡¥
¤½¤ì¤Ë¤Ä¤¤¤Æ³Ø¤Ü¤¦¡¥
 sum(n) := 1 + 2 + ... + n ¤È¤¤¤¦´Ø¿ô¤òºÆµ¢ÄêµÁ¤ò»È¤Ã¤ÆÄêµÁ¤·¤Æ¤ß¤ë¤Î¤Ç¡¤°Ê²¼¤ÎÎ㤫¤éÍý²ò¤·¤è¤¦¡¥
sum(n) := 1 + 2 + ... + n ¤È¤¤¤¦´Ø¿ô¤òºÆµ¢ÄêµÁ¤ò»È¤Ã¤ÆÄêµÁ¤·¤Æ¤ß¤ë¤Î¤Ç¡¤°Ê²¼¤ÎÎ㤫¤éÍý²ò¤·¤è¤¦¡¥
¤Þ¤º¡¤ÂоݤȤʤë´Ø¿ô¤ò¼«Ê¬¼«¿È¤ò¸Æ¤Ó½Ð¤¹·Á¤Ç¡Ö¿ô³ØŪ¤Ë¡×ÄêµÁ¤·¤Ê¤ª¤¹¡¥
¤³¤Î sum ¤ÎÎã¤À¤È¡¤(n ¤òÀµÀ°¿ô¤È¤·¤Æ)¼¡¤Î¤è¤¦¤Ë¤Ç¤¤ë¤³¤È¤ò¤Þ¤ºÍý²ò¤·¤è¤¦¡¥
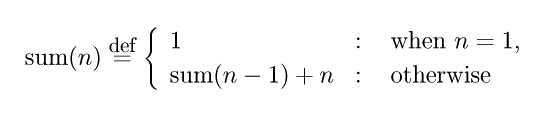
 º¸ÊÕ¤òÄêµÁ¤¹¤ë¼°¤Ç¤¢¤ë±¦Êդˡ¤º¸ÊÕ¤ÈƱ¤¸ sum ´Ø¿ô¤¬Åо줷¤Æ¤¤¤ë¤³¤È¤ËÃåÌܤ¹¤Ù¤·¡¥
º¸ÊÕ¤òÄêµÁ¤¹¤ë¼°¤Ç¤¢¤ë±¦Êդˡ¤º¸ÊÕ¤ÈƱ¤¸ sum ´Ø¿ô¤¬Åо줷¤Æ¤¤¤ë¤³¤È¤ËÃåÌܤ¹¤Ù¤·¡¥
¤³¤ÎºÆµ¢ÄêµÁ¤¬¡Ö°ÕÌ£¤ò»ý¤Ä¡×¤Ë¤Ï°Ê²¼¤Î¥Ý¥¤¥ó¥È¤¬Ëþ¤¿¤µ¤ì¤Æ¤¤¤ë¤³¤È¤¬É¬ÍפǤ¢¤ë¡¥¤è¤¯¹Í¤¨¤Æ¤ß¤è¤¦¡¥
- º¸ÊÕ¤ò±¦ÊÕ¤ÇÃÖ¤´¹¤¨¡¤¤µ¤é¤Ë±¦ÊÕ¤ÇÃÖ¤´¹¤¨¡Ä ¤È³¤±¤Æ¤¤¤±¤ë·Á¤Ë¤Ê¤Ã¤Æ¤¤¤ë¡¥
- ÃÖ´¹¤¨¤Î·«¤êÊÖ¤·¤¬¡Öɬ¤º½ª¤ï¤ë¡×¤è¤¦¤Ë¤Ê¤Ã¤Æ¤¤¤ë¡§¤³¤ÎÎã¤À¤È¡¤É¬¤º n=1 ¤Î¾ì¹ç¤ËÅþ㤹¤ë¤è¤¦¤Ë¤Ê¤Ã¤Æ¤¤¤ë¡¥
 ÄêµÁÃÖ´¹¤¨¤Î·«¤êÊÖ¤·¤¬¡Ö½ª¤ï¤é¤Ê¤¤¡×ÄêµÁ¤ò¹Ô¤Ã¤¿¾ì¹ç¡¤¥×¥í¥°¥é¥à¤Ï±Ê±ó¤ËÄä»ß¤·¤Ê¤¤! ɬ¤ºÄêµÁ¤¬ºÇ½ªÅª¤Ë´°·ë¤¹¤ë¤è¤¦¤ËÃí°Õ¤·¤ÆÄêµÁ¤·¤è¤¦¡¥
ÄêµÁÃÖ´¹¤¨¤Î·«¤êÊÖ¤·¤¬¡Ö½ª¤ï¤é¤Ê¤¤¡×ÄêµÁ¤ò¹Ô¤Ã¤¿¾ì¹ç¡¤¥×¥í¥°¥é¥à¤Ï±Ê±ó¤ËÄä»ß¤·¤Ê¤¤! ɬ¤ºÄêµÁ¤¬ºÇ½ªÅª¤Ë´°·ë¤¹¤ë¤è¤¦¤ËÃí°Õ¤·¤ÆÄêµÁ¤·¤è¤¦¡¥
¤µ¤Æ¡¤ºÆµ¢ÄêµÁ¤Î°ÕÌ£¤Ï¤ï¤«¤Ã¤¿¤È¤·¤Æ¡¤¤³¤ì¤ò¥×¥í¥°¥é¥à¤ÇÍøÍѤ¹¤ë¤Ë¤Ï¤É¤¦¤¹¤ë¤«¤ò³Ø¤Ü¤¦¡¥ ¼Â¤Ï»È¤¤Êý¤Ï´Êñ¤Ç¡¤¡Ö¤Û¤Ü¤½¤Î¤Þ¤Þ¡×½ñ¤±¤ÐÎɤ¤¡¥ Î㤨¤Ð¤³¤ÎÎã¤Î¾ì¹ç¤Ï¥×¥í¥°¥é¥à¤ò½ñ¤¯¤È¼¡¤Î¤è¤¦¤Ê´¶¤¸¤Ë¤Ê¤ë¡¥
 ¤µ¤Æ¡¤¤³¤ì¤ÇÆ°¤¯¤Î¤À¤í¤¦¤«? ¼ÂºÝ¤Ë»î¤·¤Æ¤ß¤è¤¦¡¥
¾å¤ÎºÆµ¢ÄêµÁ¤ò»È¤Ã¤Æ¡¤sum(10) ¤Ê¤É¤¬³Î¤«¤ËÀµ¤·¤¤¿ô»ú¤Ë¤Ê¤ë¤³¤È¤ò³Îǧ¤·¤Æ¤ß¤è¤¦¡¥
¤µ¤Æ¡¤¤³¤ì¤ÇÆ°¤¯¤Î¤À¤í¤¦¤«? ¼ÂºÝ¤Ë»î¤·¤Æ¤ß¤è¤¦¡¥
¾å¤ÎºÆµ¢ÄêµÁ¤ò»È¤Ã¤Æ¡¤sum(10) ¤Ê¤É¤¬³Î¤«¤ËÀµ¤·¤¤¿ô»ú¤Ë¤Ê¤ë¤³¤È¤ò³Îǧ¤·¤Æ¤ß¤è¤¦¡¥
ºÆµ¢ÄêµÁ¤Î¤Ê¤Ë¤¬´ò¤·¤¤¤Î¡© †
ºÆµ¢ÄêµÁ¤ÎºÇÂç¤ÎÍøÅÀ¤Ï¤Ä¤®¤Î¤â¤Î¤Ç¤¢¤ë¡¥
¤è¤¯¹Í¤¨¤ì¤ÐÉԻ׵Ĥʤ³¤È¤Ç¤Ï¤Ê¤¤¡¥·«¤êÊÖ¤·¤ÆÄêµÁ¤òŬÍѤ¹¤ì¤Ð¤¤¤Ä¤«É¬¤º´°·ë¤¹¤ëÄêµÁ¤Ê¤Î¤À¤«¤é¡¤¥³¥ó¥Ô¥å¡¼¥¿¤¬¤½¤¦¤·¤Æ¤¯¤ì¤ë¤À¤±¤Ê¤Î¤À¡¥ ¤·¤«¤·¡¤¤³¤ì¤¬¼ÂºÝ¤Ï¤È¤Æ¤âÊØÍø¤Ê¤³¤È¤¬Â¿¤¤¤Î¤À¡¥°Ê²¼¡¤Îã¤ÇÍý²ò¤·¤è¤¦¡¥
¥æ¡¼¥¯¥ê¥Ã¥É¤Î¸ß½üË¡ †
Æó¤Ä¤ÎÀµÀ°¿ô n, m (n >= m) ¤ÎºÇÂç¸øÌó¿ô¤ò¹Í¤¨¤è¤¦¡¥
¤³¤Î»þ¡¤¿ô³ØŪ¤Ë¼¡¤ÎÀ¼Á¤¬À®¤êΩ¤Ä(ÃΤé¤Ê¤¤¿Í¤ÏÄ´¤Ù¤è¤¦)¡¥
(mod ¤Ï¡Ö;¤ê¡×¤È¤¤¤¦°ÕÌ£¤À¤Í)
¤è¤Ã¤Æ¡¤¤³¤ì¤ò»È¤¦¤ÈÆó¤Ä¤ÎÀµÀ°¿ô n, m (n >= m) ¤ÎºÇÂç¸øÌó¿ô¤òµá¤á¤ë´Ø¿ô gcd(n,m) ¤Ë¤Ä¤¤¤Æ¼¡¤Î¤è¤¦¤ÊºÆµ¢ÄêµÁ¼°¤¬À®¤êΩ¤Ä¡¥
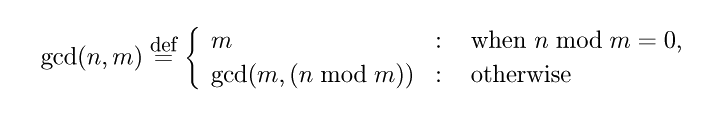
 ¤³¤Î¼°¤¬ºÆµ¢ÄêµÁ¤Î¾ò·ï¤òËþ¤¿¤·¤Æ¤¤¤ë¤³¤È¤ò³Îǧ¤·¤è¤¦.
¤³¤Î¼°¤¬ºÆµ¢ÄêµÁ¤Î¾ò·ï¤òËþ¤¿¤·¤Æ¤¤¤ë¤³¤È¤ò³Îǧ¤·¤è¤¦.
¤³¤ì¤ò¤½¤Î¤Þ¤Þ¥×¥í¥°¥é¥ß¥ó¥°¤¹¤ë¤È°Ê²¼¤Î¤è¤¦¤Ë¤Ê¤ë¡¥¤¿¤À¤·¡¤(n >= m) ¤È¤¤¤¦¾ò·ï¤òÇ°¤Î¤¿¤á¤Ë³Î¼Â¤Ë¤·¤Æ¤ª¤³¤¦¡¥¤½¤Î¤¿¤á¤Ë¤Á¤ç¤Ã¤È¤À¤±½èÍý¤¬É¬ÍפÀ¤¬¤É¤¦¤ä¤Ã¤Æ¤¤¤ë¤«¤Ï²¼¤Î¥×¥í¥°¥é¥à¤òÆɤ⤦¡¥
 ¤³¤ì¤Ç¼ÂºÝ¤ËÎ㤨¤Ð 120 ¤È 45 ¤ÎºÇÂç¸øÌó¿ô 15 ¤¬Àµ¤·¤¯µá¤Þ¤ë¤³¤È¤ò³Îǧ¤·¤è¤¦¡¥
¤³¤ì¤Ç¼ÂºÝ¤ËÎ㤨¤Ð 120 ¤È 45 ¤ÎºÇÂç¸øÌó¿ô 15 ¤¬Àµ¤·¤¯µá¤Þ¤ë¤³¤È¤ò³Îǧ¤·¤è¤¦¡¥
 ¤³¤ÎºÆµ¢ÄêµÁ¤ò¡Ö»È¤ï¤º¤Ë¡×ºÇÂç¸øÌó¿ô¤òµá¤á¤ë¥×¥í¥°¥é¥à¤¬¤É¤ì¤¯¤é¤¤ÌÌÅݤʤâ¤Î¤Ë¤Ê¤ë¤«ÁÛÁü¤·¤è¤¦.
¤³¤ÎºÆµ¢ÄêµÁ¤ò¡Ö»È¤ï¤º¤Ë¡×ºÇÂç¸øÌó¿ô¤òµá¤á¤ë¥×¥í¥°¥é¥à¤¬¤É¤ì¤¯¤é¤¤ÌÌÅݤʤâ¤Î¤Ë¤Ê¤ë¤«ÁÛÁü¤·¤è¤¦.
¤Ê¤ª¡¤ÅÓÃæ¤Î·Ð²á¤¬¤è¤¯Ê¬¤«¤é¤Ê¤¤¤È¤¤¤¦¿Í¤Ï¡¤¼¡¤Î¤è¤¦¤ËÅÓÃæ·Ð²á¤ò½ÐÎϤ¹¤ë¤è¤¦¤Ë¿ô¹ÔÉÕ¤±²Ã¤¨¤¿¥×¥í¥°¥é¥à¤òÆ°¤«¤·¤Æ¤ß¤ë¤ÈÎɤ¤¡¥
ºÆµ¢ÄêµÁ¤È¥ë¡¼¥×Áàºî¤È¤Î´Ø·¸ †
for ¤ä while ¤Ê¤É¤Î¥ë¡¼¥×¤Ç¤Ï¥ë¡¼¥×¤¬½ª¤ï¤Ã¤Æ¤«¤éºÆ¤Ó¥ë¡¼¥×¤ËÆþ¤ëÆ°ºî¤¬¼ç¤ÊÆ°ºî¤À¤¬¡¤¤³¤ì¤Ï¼«Ê¬¼«¿È¤ò¸Æ¤Ó½Ð¤¹ºÆµ¢ÄêµÁ¤ÈËܼÁŪ¤Ë¤ÏƱ¤¸¹Ô°Ù¤À¡¥
¤È¤¤¤¦¤³¤È¤Ï¡¤¥ë¡¼¥×·×»»¤ÏºÆµ¢ÄêµÁ¤Ç½ñ¤¤Ê¤ª¤¹¤³¤È¤¬¤Ç¤¤ë¤Ï¤º¤À¤·¡¤µÕ¤â¤Þ¤¿¿¿¤Î¤Ï¤º¤À¡¥
¤Ä¤Þ¤ê¡¤
¤È¤¤¤¦¤³¤È¤Ë¤Ê¤ë¡¥
 (»þ´Ö¤Ë;͵¤Î¤¢¤ë¿Í¸þ¤±) ¥æ¡¼¥¯¥ê¥Ã¥É¤Î¸ß½üË¡¤òºÆµ¢ÄêµÁ¤ò»È¤ï¤º¤Ë¥×¥í¥°¥é¥ß¥ó¥°¤·¤Æ¤ß¤è¤¦¡¥
(»þ´Ö¤Ë;͵¤Î¤¢¤ë¿Í¸þ¤±) ¥æ¡¼¥¯¥ê¥Ã¥É¤Î¸ß½üË¡¤òºÆµ¢ÄêµÁ¤ò»È¤ï¤º¤Ë¥×¥í¥°¥é¥ß¥ó¥°¤·¤Æ¤ß¤è¤¦¡¥
ºÆµ¢¤È¥ë¡¼¥×¡¤¤É¤Ã¤Á¤¬ÆÀ? †
ºÆµ¢ÄêµÁ¤È¥ë¡¼¥×·×»»¤¬ËܼÁŪ¤ËƱ¤¸¤Ê¤é¡¤¤É¤Á¤é¤òÁª¤Ö¤Ù¤¤«¤È¤¤¤¦ÌäÂ꤬¤Ç¤Æ¤¯¤ë¡¥
¤³¤ì¤Ë¤Ä¤¤¤Æ¤Ï¡¤Æó¤Ä¤Î»ëÅÀ¤¬¤¢¤ë¡¥
¤Þ¤º¡¤¥×¥í¥°¥é¥à¤Î¤ï¤«¤ê¤ä¤¹¤µ¤À¤¬¡¤¤³¤ì¤ÏÌäÂê¤Ë¤è¤ë¡¥
¥æ¡¼¥¯¥ê¥Ã¥É¤Î¸ß½üË¡¤Ê¤É¤ÏºÆµ¢ÄêµÁ¤¬¤ï¤«¤ê¤ä¤¹¤¤¤¬¡¤¼ê½ç¤ò¼¨¤µ¤ì¤ÆÍý²ò¤¹¤ë¤è¤¦¤Ê¥¿¥¤¥×¤Î·×»»¤Ï¥ë¡¼¥×¤ÎÊý¤¬¤ï¤«¤ê¤ä¤¹¤¤¤À¤í¤¦¡¥
Â礤¯½ñ¤¤¤Æ¤ª¤¯¤È¡¤
¼¡¤Ë¡¤·×»»¤Î®¤µ¤ä¥³¥ó¥Ô¥å¡¼¥¿¤Ë¤«¤«¤ëÉé²Ù¤Ë¤Ä¤¤¤Æ¤Ç¤¢¤ë¤¬¡¤
¼«Ê¬¼«¿È¤ò²¿²ó¤â¸Æ¤Ó½Ð¤¹»ÅÁȤ߾塤¹©É×̵¤·¤À¤ÈºÆµ¢ÄêµÁ¤ÎÊý¤¬Éé²Ù¤¬¹â¤¤¡¥
¤³¤ì¤òÂ礤¯½ñ¤¤¤Æ¤ª¤¯¤È¡¤
¤È¤Ê¤ë¡¥ ·ë¶É¡¤¥á¥ê¥Ã¥È¤â¥Ç¥á¥ê¥Ã¥È¤â¤¢¤ë¤Î¤Ç¡¤ºÆµ¢ÄêµÁ¤ò»È¤¦¤Ù¤¤«¤É¤¦¤«¤Ï¥±¡¼¥¹¥Ð¥¤¥±¡¼¥¹¤È¤¤¤¦¤³¤È¤Ë¤Ê¤ë¡¥
º£Æü¤ÎÁí»Å¾å¤² †
-
 ³¬¾è´Ø¿ô(factorial) n! ¤òºÆµ¢ÄêµÁ¤ò»È¤Ã¤Æ´Ø¿ô¤È¤·¤Æ¥×¥í¥°¥é¥à¤·¤è¤¦¡¥
³¬¾è´Ø¿ô(factorial) n! ¤òºÆµ¢ÄêµÁ¤ò»È¤Ã¤Æ´Ø¿ô¤È¤·¤Æ¥×¥í¥°¥é¥à¤·¤è¤¦¡¥
¤¿¤À¤·¡¤°Ê²¼¤Î¾ò·ï¤ò¤ß¤¿¤¹¤è¤¦¤Ë¤·¤è¤¦¡¥- 0! = 1, 1! = 1 ¤È¤¹¤ë¡¥
- µ¯Æ°»þ¤ËÀµÀ°¿ô¥Ñ¥é¥á¡¼¥¿ n (30¤°¤é¤¤¤òÁÛÄê)¤¬Í¿¤¨¤é¤ì¡¤0!, 1!, 2!,... n! ¤Þ¤Ç¤ò½ÐÎϤ¹¤ë¤â¤Î¤È¤¹¤ë¡¥
- ¥×¥í¥°¥é¥à¤Ï¡¤ºÆµ¢ÄêµÁ¤òÍѤ¤¤Æ·×»»¤¹¤ë¤È¤¹¤ë¡¥
¶ñÂÎŪ¤Ë¤Ï¡¤Î㤨¤Ð¥×¥í¥°¥é¥à¤Î¥Õ¥¡¥¤¥ë̾¤¬ factorial.rb ¤À¤È¤¹¤ë¤È¡¤ruby -w factorial.rb 20
¤È¤·¤Æ¼Â¹Ô¤¹¤ë¤È¡¤0! = 1 1! = 1 2! = 2 3! = 6 4! = 24 5! = 120 6! = 720 7! = 5040 8! = 40320 9! = 362880 10! = 3628800 11! = 39916800 12! = 479001600 13! = 6227020800 14! = 87178291200 15! = 1307674368000 16! = 20922789888000 17! = 355687428096000 18! = 6402373705728000 19! = 121645100408832000 20! = 2432902008176640000
¤È¤¤¤¦·ë²Ì¤¬¤Ç¤ë¤è¤¦¤Ë¤·¤í¡¤¤È¤¤¤¦¤³¤È¤Ë¤Ê¤ë¡¥
-
 Fibonacci ¿ôÎó F_0, F_1, F_2, ... ¤ò·×»»¤·¤Æ½ÐÎϤ¹¤ë¥×¥í¥°¥é¥à¤òºÆµ¢ÄêµÁ¤Ç½ñ¤³¤¦(Fibonacci ¿ôÎó¤ÎÄêµÁ¤òÃΤé¤Ê¤¤¿Í¤ÏÄ´¤Ù¤è¤¦)¡¥
¤¿¤À¤·¡¤°Ê²¼¤Î¾ò·ï¤òËþ¤¿¤¹¤â¤Î¤È¤¹¤ë¡¥
Fibonacci ¿ôÎó F_0, F_1, F_2, ... ¤ò·×»»¤·¤Æ½ÐÎϤ¹¤ë¥×¥í¥°¥é¥à¤òºÆµ¢ÄêµÁ¤Ç½ñ¤³¤¦(Fibonacci ¿ôÎó¤ÎÄêµÁ¤òÃΤé¤Ê¤¤¿Í¤ÏÄ´¤Ù¤è¤¦)¡¥
¤¿¤À¤·¡¤°Ê²¼¤Î¾ò·ï¤òËþ¤¿¤¹¤â¤Î¤È¤¹¤ë¡¥
- F_0 = 0, F_1 = 1 ¤È¤¹¤ë.
- µ¯Æ°»þ¤ËÀµÀ°¿ô¥Ñ¥é¥á¡¼¥¿ n (30¤°¤é¤¤¤òÁÛÄê)¤¬Í¿¤¨¤é¤ì¡¤F_0, F_1, F_2,... F_n ¤Þ¤Ç¤ò½ÐÎϤ¹¤ë¤â¤Î¤È¤¹¤ë¡¥
- ¥×¥í¥°¥é¥à¤Ï¡¤ºÆµ¢ÄêµÁ¤òÍѤ¤¤Æ·×»»¤¹¤ë¤È¤¹¤ë¡¥
¶ñÂÎŪ¤Ë¤Ï¡¤Î㤨¤Ð¥×¥í¥°¥é¥à¤Î¥Õ¥¡¥¤¥ë̾¤¬ fibonacci.rb ¤À¤È¤¹¤ë¤È¡¤ruby -w fibonacci.rb 30
¤È¤·¤Æ¼Â¹Ô¤¹¤ë¤È¡¤F_0 = 0 F_1 = 1 F_2 = 1 F_3 = 2 F_4 = 3 F_5 = 5 F_6 = 8 F_7 = 13 F_8 = 21 F_9 = 34 F_10 = 55 F_11 = 89 F_12 = 144 F_13 = 233 F_14 = 377 F_15 = 610 F_16 = 987 F_17 = 1597 F_18 = 2584 F_19 = 4181 F_20 = 6765 F_21 = 10946 F_22 = 17711 F_23 = 28657 F_24 = 46368 F_25 = 75025 F_26 = 121393 F_27 = 196418 F_28 = 317811 F_29 = 514229 F_30 = 832040
¤È¤¤¤¦·ë²Ì¤¬¤Ç¤ë¤è¤¦¤Ë¤·¤í¡¤¤È¤¤¤¦¤³¤È¤Ë¤Ê¤ë¡¥
 (¾åµé¼Ô¸þ¤±) ºÆµ¢ÄêµÁ¤Ç¤¢¤ê¤Ê¤¬¤é¡Ö¼Â¹Ô®ÅÙ¤¬Â®¤¤¡×¥×¥í¥°¥é¥à¤ò½ñ¤¤¤Æ¤ß¤è¤¦¡¥¤É¤¦¤¹¤ì¤Ð¤è¤¤¤À¤í¤¦¤«.
(¾åµé¼Ô¸þ¤±) ºÆµ¢ÄêµÁ¤Ç¤¢¤ê¤Ê¤¬¤é¡Ö¼Â¹Ô®ÅÙ¤¬Â®¤¤¡×¥×¥í¥°¥é¥à¤ò½ñ¤¤¤Æ¤ß¤è¤¦¡¥¤É¤¦¤¹¤ì¤Ð¤è¤¤¤À¤í¤¦¤«.
¥ì¥Ý¡¼¥È †
°Ê²¼¤Î²ÝÂê¤Ë¤Ä¤¤¤Æ¡¤¤¢¤¿¤¦¤«¤®¤ê¸ÌÀ¤ÊÄ´ºº¤È¹Í»¡¤È¼Â¹Ô¤ò¤·¡¤
ExpMath1-Report-12
¤È¤¤¤¦Âê̾¤ò¤Ä¤±¤Æ e-mail ¤Ë¤Æ¶µ´±¤Ë¥ì¥Ý¡¼¥È¤È¤·¤ÆÄó½Ð¤»¤è¡¥¤Ê¤ª¡¤³Æ¼«¤Î
- ½ê°(³ØÉô¡¤³Ø²Ê)
- ³ØÀÒÈÖ¹æ
- ³Øǯ
- »á̾
¤ò½ñ¤¯¤Î¤ò˺¤ì¤Ê¤¤¤è¤¦¤Ë.
 ¼«Ê¬¤Î¥ì¥Ý¡¼¥ÈºîÀ®¥Ä¡¼¥ë¥»¥Ã¥È¤òµºÜ¤»¤è(¤â¤Á¤í¤ó¡¤º£²ó¤Î¥ì¥Ý¡¼¥È¤â¤½¤Î¥Ä¡¼¥ë¥»¥Ã¥È¤ò»È¤Ã¤ÆºîÀ®¤¹¤ë¤³¤È)¡¥
¼«Ê¬¤Î¥ì¥Ý¡¼¥ÈºîÀ®¥Ä¡¼¥ë¥»¥Ã¥È¤òµºÜ¤»¤è(¤â¤Á¤í¤ó¡¤º£²ó¤Î¥ì¥Ý¡¼¥È¤â¤½¤Î¥Ä¡¼¥ë¥»¥Ã¥È¤ò»È¤Ã¤ÆºîÀ®¤¹¤ë¤³¤È)¡¥
¥ì¥Ý¡¼¥È²ÝÂê †
- ¼Â½¬Åù¤Ç½Ð¤Æ¤¤¿ÌäÂêÅù¤ËÂФ·¤Æ¤Î¡¤¼«Ê¬¤Î²òÅú¥×¥í¥°¥é¥à¤È¡¤¤½¤Î·ë²Ì¤ò¼¨¤»¡¥
- 1. ¤Î¥×¥í¥°¥é¥à¤ò¡Ö¾ÜºÙ¤Ë¡×²òÀ⤻¤è¡¥
about Icons, ClipArts †
For details, see
 this.
this.
