小さな問題では余り気にならないが、少し規模が大きくなってくると、少しでも計算が速い方がいい.
そのあたり、ごくごく簡単に、気づいたことを書いておこう.
そもそも論でもっと速い計算法が他にあるかも?
計算量が画期的に小さいアルゴリズムが他にないか、が最初に考えるべきことだろうなあ. 例えば、ガウス が 10歳のときのエピソードで有名な、整数を小さい方から足していくだけの問題 \begin{equation} \sum_{k=1}^n = \frac{n(n+1)}{2} \end{equation} は、左辺の式のとおりに計算すると $n-1$ 回の足し算が必要だけれども、右辺ならば足し算が 1回、掛け算が 1回、割り算が 1回 で済むので、大きな $n$ では右辺のやり方で計算する方が計算量が小さい.
「え? 当たり前だろ」と思うかもしれないけれども、これまで計算速度のことで相談された経験では、半分以上のケースで「その計算方法がどれくらいマシなのか」を全く検討した形跡がなかったので、そもそも論としてここから始めたほうが良さそうだ.
速い遅いは、実測してみないとね
意外な思い込みがあったりするので、速さが気になるときは実測データと照らし合わせながら検討していく必要がある. こうした用途には、BenchmarkTools package が Julia 開発者界隈ではよく使われている (例: Julia 0.5 Highlights) ので、これを使うようにしていくと良さそうだ.
では、使ってみよう.(このパッケージをインストールしていない人は Pkg.add("BenchmarkTools") してから) まずは使用宣言.
using BenchmarkTools
使い方は簡単で、実行する関数の前に @benchmark とつけるだけでいい.
上の足し算を例として以下のようにやってみよう.
direct_sum(n) = sum(k for k in 1:n)
bino(n) = n*(n+1)/2
として、左辺と右辺とをそれぞれ関数にしておこう. 次に、確認だ.
direct_sum(10), bino(10)
(55,55.0)
確かに動作は正しいようだ.
では、それぞれの測定を行ってみよう.まずは左辺だ.
a = @benchmark direct_sum(100) # 再利用できるように、結果に名前 "a" をつけておく
BenchmarkTools.Trial:
memory estimate: 48.00 bytes
allocs estimate: 2
--------------
minimum time: 65.443 ns (0.00% GC)
median time: 70.149 ns (0.00% GC)
mean time: 80.453 ns (6.71% GC)
maximum time: 7.369 μs (95.80% GC)
--------------
samples: 10000
evals/sample: 1000
time tolerance: 5.00%
memory tolerance: 1.00%
ふ~む、平均で 80ns かかるんだなあ. では、右辺はどうかな.
b = @benchmark bino(100) # この結果にも名前をつけておこう
BenchmarkTools.Trial:
memory estimate: 0.00 bytes
allocs estimate: 0
--------------
minimum time: 2.138 ns (0.00% GC)
median time: 2.139 ns (0.00% GC)
mean time: 2.386 ns (0.00% GC)
maximum time: 180.504 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 1000
time tolerance: 5.00%
memory tolerance: 1.00%
こちらの平均は 2ns というところか.
平均だけ見るなら、この結果に mean()を適用すれば良いので(BenchmarkTools のマニュアル を読むと、この結果の処理のしかた、便利ないろんなコマンド等が載っている), 次のような感じだ.
mean(a)
BenchmarkTools.TrialEstimate:
time: 80.453 ns
gctime: 5.394 ns (6.71%)
memory: 48.00 bytes
allocs: 2
time tolerance: 5.00%
memory tolerance: 1.00%
mean(b)
BenchmarkTools.TrialEstimate:
time: 2.386 ns
gctime: 0.000 ns (0.00%)
memory: 0.00 bytes
allocs: 0
time tolerance: 5.00%
memory tolerance: 1.00%
結果を比較するコマンド ratio() もあるので試してみよう.
ratio( mean(a), mean(b) )
BenchmarkTools.TrialRatio:
time: 33.72418729022912
gctime: Inf
memory: Inf
allocs: Inf
time tolerance: 5.00%
memory tolerance: 1.00%
この場合、平均で右辺のほうが34倍弱速い、ということになりそうだ. $n$ を変えるとどうなるか、ちょっと見てみようか.
そのために、この結果のオブジェクトがどうなっているのか、ちょっと調べておこう.
オブジェクトの構造は dump() で次のように見ることが出来る.
dump(mean(a))
BenchmarkTools.TrialEstimate
params: BenchmarkTools.Parameters
seconds: Float64 5.0
samples: Int64 10000
evals: Int64 1000
overhead: Float64 0.0
gctrial: Bool true
gcsample: Bool false
time_tolerance: Float64 0.05
memory_tolerance: Float64 0.01
time: Float64 80.45271460000002
gctime: Float64 5.3943826
memory: Int64 48
allocs: Int64 2
すると、time 要素に時間が入っているようだ.よって .time をつければ取り出せるはず.試しておこう.
mean(a).time
80.45271460000002
これでうまくいきそうなので、例えば次のようにして、様子を見ることができそうだ(計算時間はちょっとかかる).
d_sq, b_sq = [], []
for n in 10:5:100
a = @benchmark direct_sum($(n)) # マクロの展開を上手にやっていないようなので、$ を使って「変数埋め込み」を明示しておく
b = @benchmark bino($(n))
push!(d_sq, mean(a).time)
push!(b_sq, mean(b).time)
end
using Plots
gr()
plot( 10:5:100, hcat(d_sq, b_sq) )
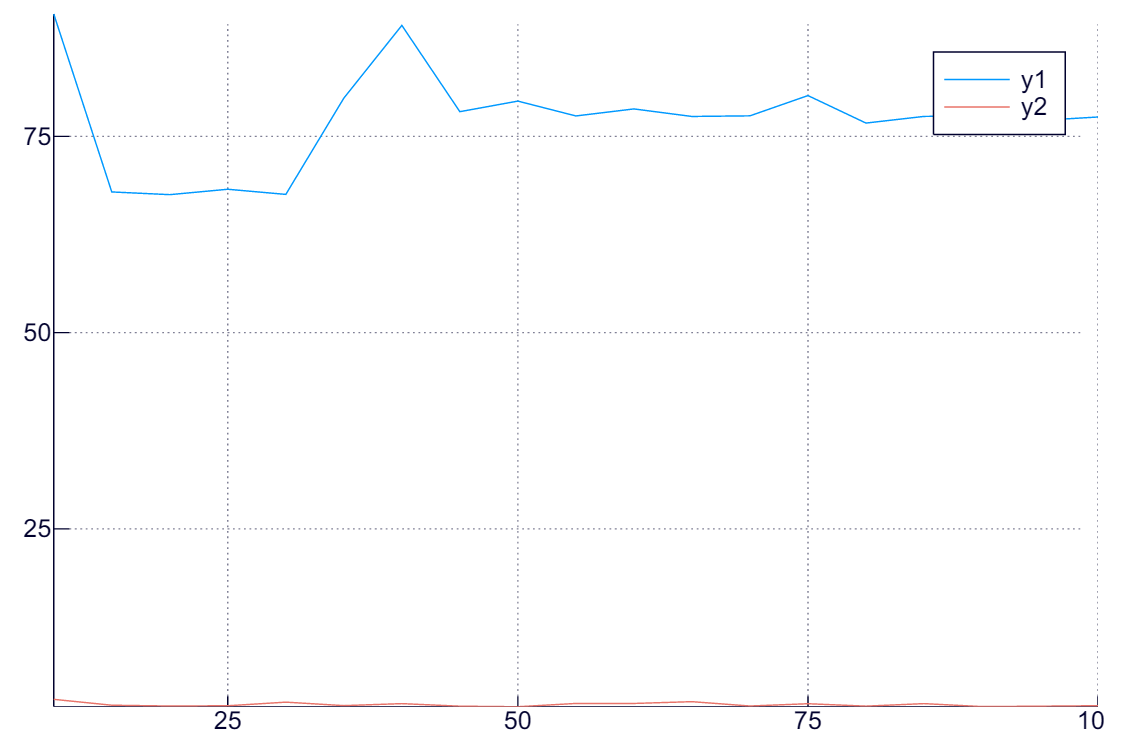 どうやらこの程度の規模だと、$n$ の大小は計算時間にほとんど影響がないようだということがわかる.
それどころか、試してみると分かるが、実はこの問題は $n$ の大小にほぼ影響を受けない(コンパイラが相当に賢いことをやっている?).
どうやらこの程度の規模だと、$n$ の大小は計算時間にほとんど影響がないようだということがわかる.
それどころか、試してみると分かるが、実はこの問題は $n$ の大小にほぼ影響を受けない(コンパイラが相当に賢いことをやっている?).
直感と異なるが事実はこうだということが、このように実測データから示されるので、こうした実測は重要だ.
ちなみに、左辺を次のように定義するとどれくらい速い・遅いだろうか.先に予測してから、実測して確認してみよう.
function direct_sum2(n)
r = 0
for k in 1:n
r += k
end
return r
end
BenchmarkTools に頼らないで実測するには
他にも、tic(), toc() コマンドや @time マクロを使う方法もある.
こちらの方が、マクロ的には「丈夫な作り」(= 文法上の制限が緩い) なので、まずはこちらで、というのでも良いだろう.
ただしこの場合、複数回計算して平均をとったりするのは自力で行う必要があるなあ. 使い方の例を示しておこう.
tic()
direct_sum(10_000_000) # 位取りが分かりやすいように、_ を使っても良い
toc()
elapsed time: 0.000136448 seconds
0.000136448
@time direct_sum(10_000_000)
0.000003 seconds (6 allocations: 208 bytes)
50000005000000
みるとわかるが、このように「すごく速い計算」は、測定方法自体が余計にかけてしまう時間の影響が大きいので、上のように測定結果にばらつきが大きいので注意しよう.
Julia の文法による話
定数は const 宣言しておこう
定数とそうでない変数の参照速度は意外に違うため、変化しない量には const をつけて定数だと宣言しておくとプログラムの実行速度があがることなる.
「実測に影響するほどか?」と思うかもしれないが、これがなかなか馬鹿にならない(あるプログラムでは、これだけで 10倍以上高速化した).簡単な例でみてみよう.
a = 5.0
r = 0.0
@time for n in 1:100_000_000
r += sin(a)
end
8.958159 seconds (200.00 M allocations: 2.980 GB, 2.90% gc time)
なにもしない結果が上で、const をつけた結果が下である.
const b = 5.0
r = 0.0
@time for n in 1:100_000_000
r += sin(b)
end
7.171755 seconds (200.00 M allocations: 2.980 GB, 3.68% gc time)
というわけで、なるべく const を使おうというお話.
関数は型安定(type-stable)にしておこう
型安定性(type-stability)というのは、関数の性質で、
「関数の出力の型が、入力変数の型だけに依存し、入力変数の数値に依らない」
ことを指す概念だ. multiple dispatch 言語特有の概念で初めて見る人も多いと思うが、 型安定だとコンパイラがその型ごとにチューンしたバイナリを作って上手に配置できるため、高速実行が可能になるという利点がある.
例を見てみよう. 例えば、入力値が正のときだけその値を返し、負の時はゼロを返すような関数を作るとしよう. そして、ごく普通に、次のように作ったとしよう.
function positive(x)
if x < 0
return 0.0
else
return x
end
end
しかしこれだとちょっとまずい. 入力変数 $x$ が整数のときを考えてみよう. $x$ が正ならば出力値は $x$ そのもので整数なのに、負のときは 0.0 で浮動小数になってしまう. つまり、この関数の出力値の型は $x$ の値そのものに依存してしまい、型安定ではない.
こういうときは、例えば入力変数と同じ型の 0 を返す関数 zero() という関数を使って次のようにすれば良い.
これならこの関数は入力変数と同じ型を常に返すことになるから、型安定になっている.
function positive_safe(x)
if x < 0
return zero(x)
else
return x
end
end
実際の速度差を見てみよう. べき乗あたりが型によってバイナリコードが大きく違いそうなので、べき乗計算を使って型安定性の影響を見てみよう. まず最初は、型安定でない関数を使った場合だ.
@time for n in 1:100_000_000
a = 2^( positive(-n) + 1 )
end
7.094579 seconds (200.00 M allocations: 2.980 GB, 5.80% gc time)
そして次が型安定の場合だ.
@time for n in 1:100_000_000
a = 2^( positive_safe(-n) + 1 )
end
1.501520 seconds
型安定だと随分と高速だということが分かる.
これに対し、「え、ベキの肩に乗っている変数が浮動小数か整数かが違うだけでは?」と思う人もいるだろうから、次のようにして、「型安定な関数を使う and べき乗の肩は浮動小数」という状況もチェックしてみよう.
@time for n in 1:100_000_000
a = 2^( positive_safe(-n) + 1.0 )
end
2.865138 seconds (100.00 M allocations: 1.490 GB, 4.59% gc time)
この場合でもやはりこちらの方が随分と高速だ.バイナリ実行の中で変な場合分けが生じなくて済んでいるのだろう.
コンパイラにとって、「実行した先の型がはっきりとわかる」というのは重要だということがよく分かる.
抽象度の低い型の方がなにかと速いよ
Julia の型には抽象度とでもいうべき概念があり、抽象度が高いほうが融通が効いてプログラムも書きやすいが、必要なメモリも大きめで実行速度も遅い. よって、速度が気になるならばなるべく抽象度の低い型を選ぶべき、ということになる(その分、プログラムの柔軟性が下がるが).
これも試してみよう. まず、 Julia マニュアル “Types” ページの “Abstract Types” 項目 によれば、 Julia の「数値型」で一番抽象度が高いのは Number なので(これより上は文字列なども混じってくる)、これと、具体型の一つの Int64 で計算速度に違いが出るか、チェックしてみよう.
例えば、配列の中身の自乗和を計算するような関数を次のように用意する.
function sqsum(x)
r = zero(x[1])
for n in 1:length(x)
r += x[n]^2
end
return r
end
これは見て分かるように型安定なので安心して使える.
さて、Number 型の配列と、Int64 型の配列を例えば次のように用意しよう.
a = Array(Number, 10)
a .= collect(1:10)
b = Array(Int64, 10)
b .= collect(1:10)
どちらも中身は実質的には同じ、$[ 1, 2, 3, … , 10 ]$だ. これらそれぞれに対して、上の自乗和関数を適用してみよう.計算過程は全く同じはずだ.
@benchmark sqsum(a)
BenchmarkTools.Trial:
memory estimate: 0.00 bytes
allocs estimate: 0
--------------
minimum time: 653.612 ns (0.00% GC)
median time: 689.663 ns (0.00% GC)
mean time: 696.479 ns (0.00% GC)
maximum time: 3.761 μs (0.00% GC)
--------------
samples: 10000
evals/sample: 178
time tolerance: 5.00%
memory tolerance: 1.00%
ふむ、Number 配列相手だと平均で約 700ns かかるわけだな. では Int64 だとどうだろう.
@benchmark sumsq(b)
BenchmarkTools.Trial:
memory estimate: 0.00 bytes
allocs estimate: 0
--------------
minimum time: 70.778 ns (0.00% GC)
median time: 71.217 ns (0.00% GC)
mean time: 74.379 ns (0.00% GC)
maximum time: 398.899 ns (0.00% GC)
--------------
samples: 10000
evals/sample: 979
time tolerance: 5.00%
memory tolerance: 1.00%
こちらは平均で 74ns なので、おおよそ 10倍程度速いということになる. このように、型に気をつけるとだいぶ速くなるはずだ.
並列計算
Julia はいくつかの並列計算法をネイティブでサポートしている. さらに、GPGPU などの特殊なハードウェアに対してもそれぞれ専用のパッケージが多数存在するので、自分の計算機環境の能力を引き出すことがきっと可能なはずだ.
SIMD 計算(ベクトル計算)
複数の並んだ同種の計算について、一度に計算を行う機能がハードウェアによってサポートされている場合がある. 一昔前のベクトル計算というやつがそうだし、今だとこれは SIMD とよばれる機能として、通常の CPU 自身に組み込まれている.
Julia は、この機能を直接使うことが出来る.
方法は簡単で、そうした同種の計算が並ぶ形になる for 文の頭にマクロ @simd を適用するだけだ.
以下、例を見てみよう.そうだなあ、ベクトル同士の単なる内積を対象としてみよう. まず、そうした関数を普通に定義する.
function inner( x, y )
r = zero( x[1] )
for i in 1:length(x)
@inbounds r += x[i] * y[i] # @inbounds は配列の境界チェックを省略する指示
end
return r
end
次に、@simd を使った関数を用意しよう.
function inner_simd( x, y )
r = zero( x[1] )
@simd for i in 1:length(x) # この for 文に @simd をつけるだけでよい.
@inbounds r += x[i] * y[i]
end
return r
end
そして、これらを比較してみよう.
x, y = randn(1000), randn(1000)
@benchmark inner(x,y)
BenchmarkTools.Trial:
memory estimate: 16.00 bytes
allocs estimate: 1
--------------
minimum time: 1.155 μs (0.00% GC)
median time: 1.198 μs (0.00% GC)
mean time: 1.224 μs (0.00% GC)
maximum time: 13.388 μs (0.00% GC)
--------------
samples: 10000
evals/sample: 10
time tolerance: 5.00%
memory tolerance: 1.00%
単純な積和だと、1.2μs ほどかかるようだが、
@benchmark inner_simd(x,y)
BenchmarkTools.Trial:
memory estimate: 16.00 bytes
allocs estimate: 1
--------------
minimum time: 425.583 ns (0.00% GC)
median time: 438.482 ns (0.00% GC)
mean time: 453.468 ns (0.14% GC)
maximum time: 6.902 μs (91.90% GC)
--------------
samples: 10000
evals/sample: 199
time tolerance: 5.00%
memory tolerance: 1.00%
この場合、@simd をつけるだけで、倍以上速くなることが分かる.
なお、この効果の強さはハードウェア(CPU など)に強く依存するので(例えば、同じ例でも Juliabox.com だと3倍以上速くなる)、自分のマシンでも試してみることを強くおすすめする.
複数プロセスによる実行
Julia はプロセスを複数立ち上げて、それらに仕事を分配して作業させることが出来る. このとき、一つが master になり、他は worker とよばれる、いわば下請けプロセスになる. この非対称性のおかげで、メッセージは一方向通信で済むし、プログラムが随分と自然に書けるようになる(この方向はおそらく正しくて、例えば、MPI は最近になって一方向通信をサポートしたりしている).
しかもこの worker プロセスは同じマシン上になくても良いので、その気になれば cluster 上で Julia で大きな計算ができることになる.
まず、最初に、必要な数の worker プロセスを立ち上げよう.単純に addprocs(数) とすると、そのマシン上にさらにその数だけの julia worker プロセスが追加で起動する.
addprocs(5)
このとき、addprocs() の引数に自分以外のマシン情報を書くと、その指定されたマシン上で worker プロセスが起動して、こちらから使えるようになる.
ちなみに、procs() とすると、今いくつのプロセスが挙がっているかがわかる.
使わなくなった worker プロセスを停めるには rmprocs() が使える.まあ、そんなに使うことはないだろうが.
@parallel for (単純な並列計算をさせる)
単純な計算結果をただかき集めるような場合は、@parallel for と呼ばれるマクロを使うだけで良い.
すると、(背後で) worker プロセスにそれが適切に配分されて、結果が master に集められる.
例として、true/false を結果として出すような乱数を振らせて、true だった回数をカウントすることを考えてみよう. いわばコイントスだ.
まず、これをシングルプロセスで行う、普通の関数を書いておこう.
function coin(n)
num = 0
for i in 1:n
num += Int(rand(Bool))
end
return n
end
次に、@parallel for を使う関数を用意する.この場合は、かき集めた結果を「足しあわせる」ので、(+) という関数が挟まれることに注意しよう.
function coin_p(n)
num = @parallel (+) for i in 1:n # これが @parallel for 構文
Int(rand(Bool))
end
return n
end
早速、ベンチマークだ.
n = 200_000_000
@benchmark coin(n)
BenchmarkTools.Trial:
memory estimate: 16.00 bytes
allocs estimate: 1
--------------
minimum time: 586.634 ms (0.00% GC)
median time: 592.540 ms (0.00% GC)
mean time: 600.422 ms (0.00% GC)
maximum time: 662.216 ms (0.00% GC)
--------------
samples: 9
evals/sample: 1
time tolerance: 5.00%
memory tolerance: 1.00%
シングルプロセスだと、600ms ほどかかるようだ. では、複数プロセスだとどうだろうか.
@benchmark coin_p(n)
BenchmarkTools.Trial:
memory estimate: 62.88 kb
allocs estimate: 694
--------------
minimum time: 199.298 ms (0.00% GC)
median time: 215.632 ms (0.00% GC)
mean time: 219.853 ms (0.00% GC)
maximum time: 260.984 ms (0.00% GC)
--------------
samples: 23
evals/sample: 1
time tolerance: 5.00%
memory tolerance: 1.00%
220ms で済んでいることがわかる.約3倍ほど高速化されたということになる(JuliaBox だと、10以上にプロセスを増やすと、5倍程度には速くなる).これはありがたい. ちなみに、いくつプロセスを使えばいいかという問題は結構微妙だ.少し試してみる必要があるだろう.
pmap (map の並列化)
map 関数は同種の対象に同じ関数を適用するわけだから、こうした並列化にかなり適しているのではないだろうか.
実際、そうするための専用命令があり、pmap() がそれである.使い方は map() と全く同じだ.
この例としてあちこちで挙がっている、特異値分解 svd を使ってみよう.
まず、対象の行列をたくさん用意する.
a = [ rand(100,100) for n in 1:100 ]
それから、map, pmap それぞれのケースで測定してみよう.
@benchmark map(svd, a)
BenchmarkTools.Trial:
memory estimate: 54.74 mb
allocs estimate: 2402
--------------
minimum time: 600.345 ms (0.27% GC)
median time: 609.244 ms (0.53% GC)
mean time: 624.458 ms (2.71% GC)
maximum time: 713.380 ms (16.11% GC)
--------------
samples: 9
evals/sample: 1
time tolerance: 5.00%
memory tolerance: 1.00%
@benchmark pmap(svd, a)
BenchmarkTools.Trial:
memory estimate: 16.16 mb
allocs estimate: 23244
--------------
minimum time: 252.644 ms (0.00% GC)
median time: 283.941 ms (0.70% GC)
mean time: 298.224 ms (0.64% GC)
maximum time: 382.588 ms (0.81% GC)
--------------
samples: 17
evals/sample: 1
time tolerance: 5.00%
memory tolerance: 1.00%
この場合、倍以上に高速化されていることが分かる.
worker プロセスに命令を個別に与える
複雑な問題はこうする必要があるだろう.
基本は簡単で、@spawnat で worker を指定して作業をさせ、結果を fetch で受け取るだけである.
こうなると速いかどうかはプログラム自身の問題になってしまいなかなか厄介なので、ここでは簡単な例だけ示しておこう.
# worker 2 に、randn(1000,1000) という仕事をさせて、その結果に r1 という名前をつけておく
r1 = @spawnat 2 randn(1000,1000)
Future(2,1,877031,Nullable{Any}())
# worker 3 に、r1 の結果を参照してそれに expm という関数を適用する計算をさせる.この結果を r2 と名付けておく.
r2 = @spawnat 3 expm(fetch(r1))
Future(3,1,877032,Nullable{Any}())
# master が結果 r2 を取得する.
fetch(r2)
1000×1000 Array{Float64,2}:
-1.61493e11 -2.7476e10 -8.08821e10 … -6.94514e11 5.39723e11
-1.63468e11 3.08028e11 -3.44445e11 9.16051e11 2.68904e10
...
各種パッケージを使う
Julia のオフィシャル web のパッケージ部分には並列計算や、GPGPU を使うパッケージが大変多く登録されている. 例えば、 ParallelAccelerator というパッケージ は Intel Lab が提供しているパッケージで、 これは C++ と OpenMP をバックエンドに使って高速並列計算を可能とするもので、 うまくはまると大変な高速化が可能である.
An introduction to ParallelAccelerator.jl という記事に詳細が書いてあるが、例えば、1CPU (36 core) のマシンで 400倍ほどの高速化に成功した例などが載っている. ある程度良いハードウェアが使える人は、こうしたパッケージを積極的に使っていくと良さそうだ.