魔法の加速法

意外に知られていない, 加速法ってやつについてちょろっと書いとこう． ほんのわずかな計算コストでより良い情報を引き出せる可能性が結構高いオトクな技法で、そういう意味でまあ魔法みたいなもんだな． 知っておいて損はないと思うぞ．

で、加速法とは何かっつうと、収束する ¹ 数列をもとにして 「もっと速く収束する数列を作る」 数学的な方法、っつうことになる．

そして「計算なり観測なり実験なりを進めて、収束していると期待される数字の列がデータとして得られるんだ．この収束先が求めたい値なんだ」 という、収束先がわからない状況が、応用として想定されるシチュエーションだ． で、そのまま計算なりを進めるよりも、手元に既にあるデータを加速法で変換したほうが低コストでより良い収束先の近似値が得られるかもよ？ というのが加速法の使い方、ということになる．

そして実は、加速法ってのはたくさんある ² んだけど、ここでは導入としての Richardson 加速と Aitken 加速を紹介しておこう． ちなみにこの Aitken 加速ってのはかの関孝和が円周率の近似計算に用いた…んだそうな．よくしらんけど．

サンプル数列を用意するべ

例えば、 \begin{equation} a_n = 2.5 + 1000 \cdot \frac{(0.9)^n}{\sqrt{n+1}}, 　　　 n = 1,2,\cdots \end{equation} という要素 $a_n$ からなる数列 $a$ をサンプルにしてみよう． そして、この $2.5$ という収束先を如何に推測するか、というストーリーを想定するわけだ．

まず、

const N = 60
const α = 2.5
const C = 1000.0
const rate = 0.9
a = [α + C * (rate^n) / sqrt(n+1)  for n in 1:N] 

という感じで模擬データが作れるな ³ ． すると

60-element Array{Any,1}:
 638.896  
 470.154  
 367.0    
 295.917  
 243.567  
 203.366  
 171.603  
 145.989  
 125.013  
 107.631  
  93.0893 
  80.8319 
  70.4342 
   |      
   3.30984
   3.22167
   3.14323
   3.07342
   3.01128
   2.95595
   2.90667
   2.86278
   2.82367
   2.78883
   2.75777
   2.73008

という感じで数列 $a$ が得られる． ちなみにこいつの収束の様子をグラフで見ておこう．

using PyPlot
plot(a)

として 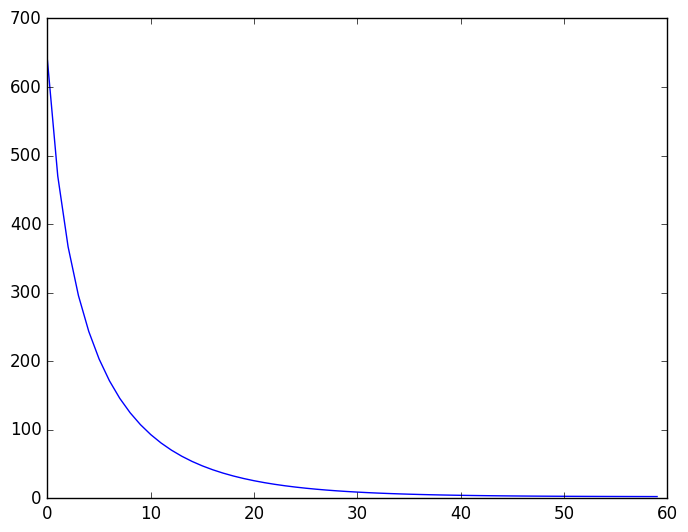という感じのプロットが得られる． 最初の方のデータはあまり良くないだろうから、 最後の方の 20個程度のデータを見てみよう．

plot(a[end-20:end])

として

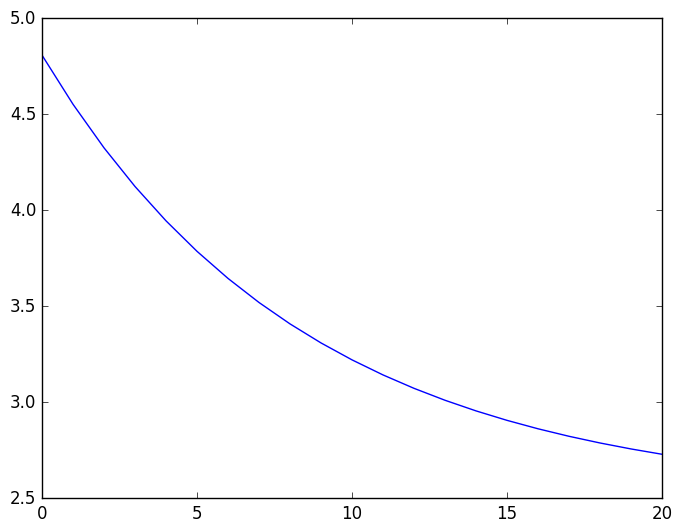
を得る． じりじりとどこかへ収束しそうな気配はあるが, 真の収束先 $\alpha = 2.5$ を推測するのはまだ無理があるかなあ． 実際、最後の値 $2.73008$ も収束値の近似値としてはまだ 1割程度の誤差 を含んでいる． そこで、もうちょいなんとかならんかね？ というところで、加速法の出番だ．

Richardson 加速

Richardson 加速ってのは、未知の収束先 $\alpha$ をもつ数列 $\{ x_n \}$ が、既知の定数 $\gamma$ と未知の係数 $C$ を使って \begin{equation} x_n \cong \alpha + C \gamma^n, 　　n = 1,2,\cdots \label{eq:assumption} \end{equation} と表されるケースを想定している加速法だ．

さすがに、この形は単純すぎるし、「$\gamma$ がわかっている」という前提も現実問題ではちょっと非現実的だが、実はそこは気にしないでいい． というのも、この Richardson 加速をベースにして、他の「より実用的な」解法を考えることができるのだ． というわけで、この Richardson 加速は「加速法の考え方の初歩」と思っておけばいいんじゃないかな．

さて、話を戻すと、$\gamma$ がわかってるだけにストーリーは簡単で、データを二つ使って未知係数 $C$ を消去して \begin{equation} \alpha \cong \frac{ x_{n+1} - \gamma x_n }{ 1 - \gamma } \end{equation} と書けるため、新しい数列 $\{ y_n \}$ を \begin{equation} y_n \defeq \frac{ x_{n+1} - \gamma x_n }{ 1 - \gamma }, 　　n = 1,2,\cdots \label{eq:richardson} \end{equation} として作れば、これはもとの $\{ x_n \}$ よりも速く収束先 $\alpha$ に近づくことが期待できるというわけだ．

で、このようにして新しい数列を作ることが Richardson加速ってわけだな．

さて、先のサンプルデータ(これは Richardson 加速の想定している式の形になっていないが)に対して実際に Richardson加速をしてみよう．

function rcs(r, x, n)
    return (x[n+1]-r*x[n])/(1.0-r)
end

で Richardson加速による変換を実装して、 上のサンプルデータの rate から $\gamma \cong 0.9$ とみなして、

b = [rcs(rate,a,n) for n in 1:N-1]

とすれば新しい数列 $\bm{b}$

59-element Array{Any,1}:
 -1048.53   
  -561.383  
  -343.832  
  -227.586  
  -158.441  
  -114.257  
   -84.5407 
   -63.7705 
   -48.813  
   -37.7814 
   -29.4852 
   -23.1445 
   -18.2318 
     |     
     2.41778
     2.42819
     2.43724
     2.44513
     2.45199
     2.45798
     2.4632 
     2.46775
     2.47173
     2.47521
     2.47825
     2.48091

が得られるわけ、だな． 最初の方はともかく、最後の方はだいぶ 2.5 に近そうなので、先と同様に最後の 20個ほどのデータをプロットして見てみますか．

plot(b[end-20:end])

として

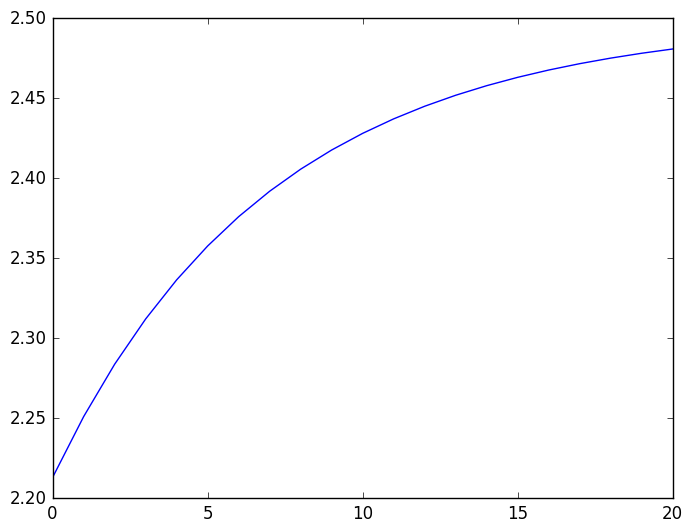
という感じになるが、これは確かに、もとのデータよりもだいぶ良くなっているな． 最後の値 $2.48091$ も、誤差はたったの 1% 程度なので、Richardson 加速によってなんと 精度が10倍になった ．ん～、素晴らしい．

…しかしまあ、先にも書いたように、定数 $\gamma \cong 0.9$ を知っていればこその Richardson加速なわけで． まあ普通はこの定数もわからんわけで、その場合は Richardson加速は使えないというオチがついてくる． そこで、次の Aitken 加速の出番だ．

Aitken 加速

Aitken 加速の前提は Richardson 加速のそれによく似ているが、Aitken 加速では 定数 $\gamma$ も未知やで ということを前提にするところが違う． これで ぐんと実用度が上がる というものだ．

で、じゃあどうする？ という話だが、これまた簡単で、 式 $(\ref{eq:assumption})$ から \begin{equation} \gamma \cong \frac{ x_{n+2} - x_{n+1} }{ x_{n+1} - x_n } \end{equation} と言えるので、これを 未知の定数 $\gamma$ の推定値として Richardson 加速を使えばいい ． つまり、この $\gamma$ の推定値を 式 $(\ref{eq:richardson})$ に代入すればいいということになるので、結果として、 \begin{equation} z_n \defeq x_n - \frac{ ( x_{n+1} - x_n )^2 }{ x_{n+2} - 2 x_{n+1} + x_n }, 　　n = 1,2,\cdots \label{eq:aitken} \end{equation} とすればいい、というのが Aitken 加速、ということになる．これまた単純だな！

というわけでやってみよう． まず

function aitken(x,n)
    return x[n] - ((x[n+1]-x[n])^2 / (x[n+2] - 2*x[n+1] + x[n]))
end

として Aitken 加速を実装して、これをもとの数列 $\bm{a}$ に

c = [aitken(a,n) for n in 1:N-2]

として適用して新しい数列 $\bm{c}$ を以下のように得る．

58-element Array{Any,1}:
 204.766  
 138.364  
  97.2698 
  70.3492 
  52.0492 
  39.27   
  30.1562 
  23.543  
  18.6737 
  15.0425 
  12.3044 
  10.2192 
   8.61692
   |      
   2.51394
   2.51198
   2.5103 
   2.50887
   2.50764
   2.50658
   2.50568
   2.5049 
   2.50423
   2.50366
   2.50316
   2.50274

で、

plot(c[end-20:end])

として最後の 20個ほどのデータをプロットしてみると

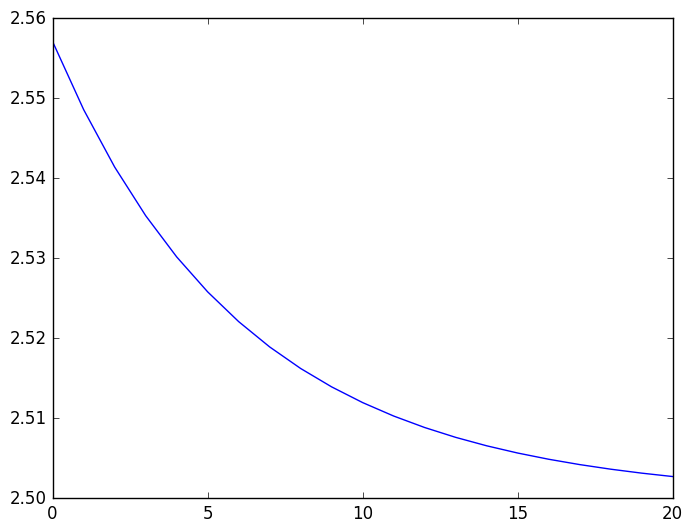
となっていて、Richardson 加速よりさらに良くなっている． しかも Richardson 加速と違って、なにか係数を知っていないといけないという縛りもない．

最後の値 $2.50274$ の誤差はもう 0.1% 程度なので、元データに比べて Aitken 加速で 精度が 80倍程度良くなっている！

それに、計算式 $(\ref{eq:aitken})$ をみればわかるが、Aitken 加速をするための計算コストはほぼタダみたいなものだ． ということは Aitken 加速は

• タダみたいな計算コスト
• 事前知識不要、縛りなし
• 精度がすげー良くなる可能性高し

という、嘘みたいな美味しい話なのだ． これはやらないほうが損というものだろう． もしも良い結果が出なくても、タダみたいな計算コストだから損はないしな．

しかも、加速は重ねがけできるぜ

加速法で得られた数列は、もとのものより速く収束するわけだが、なんと、この結果にさらにもう一回、もう二回、とどんどん加速法を重ねていくことが出来る． しかもそれでどんどん結果が良くなる可能性があるので、これはなんとも簡単でお徳な話、ということになる．

やってみよう． さっきの Aitken 加速の結果の数列 $\bm{c}$に、再度 Aitken 加速を適用して、数列 $\bm{d}$ を作ってみよう．

d = [aitken(c,n) for n in 1:N-4]

56-element Array{Any,1}:
 30.5453 
 19.2164 
 13.2019 
  9.68969
  7.49454
  6.05452
  5.07625
  4.3942 
  3.90911
  3.55863
  3.3021 
  3.11229
  2.97051
  |      
  2.5006 
  2.5005 
  2.50042
  2.50035
  2.5003 
  2.50025
  2.50021
  2.50018
  2.50015
  2.50013
  2.50011
  2.50009

数字を見ると、明らかに大変良くなっている！
急いでプロットしてみるべし．

plot(d[end-20:end])

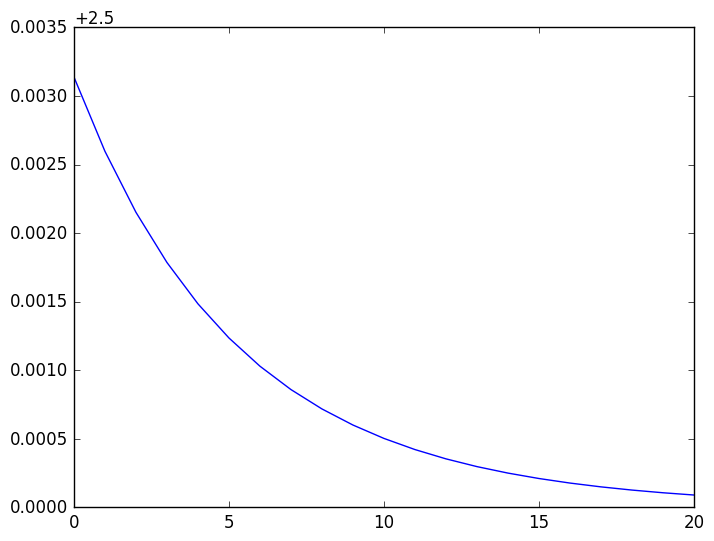
ん～、これはすごい、すごいぞ．もう、収束先 $\alpha = 2.5$ がみえみえだ． そして最後の値 $2.50009$ の誤差は 0.003 % ほどしかない．精度は 2500倍良くなった！

これを繰り返すだけで、どれだけ精度が良くなるか、想像してみるべし．

大事な大事な結論

というわけで、「なんか数列データがあるんだよなあ」というときは何も考えず Aitken 加速(のような汎用加速法)を試しに適用してみるのはけして悪い手じゃないので、覚えておくといいかも、だ．