Photo by Alina Grubnyak on Unsplash

人工知能(Artificial Intelligence: AI) 技術

人工知能というのは情報技術の長年の夢の技術であり，これまで長い歴史がある． 昨今は Deep Learning に代表される機械学習がたいへんに注目を集めているが，他にも多くの要素技術があり，それぞれに得手不得手がある． これらについて，AIに関する機械学習とその他の要素技術について今回から学んでいこう．

Deep Learning (深層学習)入門

今回はまずは近年たいへんに発達し注目されている機械学習技術の一つである Deep Learning について，その本質を簡単に学ぼう． 流行っていることもあって機械学習のライブラリ・フレームワークは多く存在するが，今回はそうしたものを使わずに自分でプログラムして内容を理解する一助としよう．

この Deep Learning というのは，多層の neural network (NN と略されることも多い) を数学的にモデリングして利用するもので， この層の数が多くても内部パラメータを問題なくチューンできることから名前に deep がつくものである． この技術によって画像分類問題で大変画期的な結果が出て以来，大変 hot な分野であることは間違いない．

しかし，その開発が大変勢いある分野であるため，細かい技術論にまどわされて「全体がよくわからない」という者も多いだろう． 先に書いたように，今回は基本的な考え方を理解できるよう，解説と素のプログラミングを重視してすすめよう．

全体像

全体像を示そう． まず，機械学習でやりたいことは何かというと，

やりたいこと = 入力を与えると良い答を返す関数を作ること

なのだ． これがうまくできれば，われわれが知能を使って行っている作業のうち多くをコンピュータに代わりにさせることができる，というわけだ¹．

そして，機械学習の様々な技術は，この「関数を作り，改善すること」を如何に上手にやるか，という技術なのだ．

今回扱う deep learning では，関数を neural network で作り，そのパラメータを改善していく技術だ． シンプルな仕組みながらこれが大変うまくいく問題が多く，そのために期待されているのだ．

Neural Network

ニューロン(神経細胞)の構造図, license:public domain, created by LadyofHats

Neural Network とは，上の図のような神経細胞(ニューロン)によって構成された神経網を真似たシンプルな数学モデルだ．

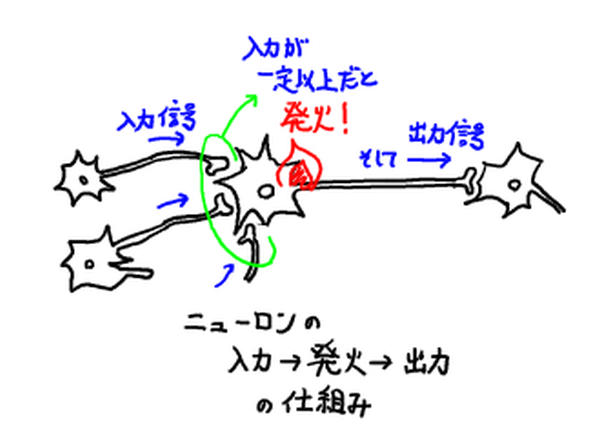
もとの神経網の仕組みをおおまかにいうと，まず，ニューロンの電気信号が軸索を通じてそのニューロン末端のシナプスに届き，その結合を介して信号を他のニューロンに伝えるようになっている． ニューロンはそのようにして複数のニューロンからやってきた信号を受け取るわけだが，集まった信号が一定以上の大きさであれば「反応(興奮や発火と呼ばれる)」して新たに電気信号を作り，他のニューロンへ信号を伝える． あとはこの繰り返し，という仕組みで，この「網の形」と「シナプス結合の強さ」等々によって情報処理がうまくいくようになっている，と考えられている．

これをモデル化して，いわゆる有向グラフの「ノード」をニューロンの信号受信&処理部分とすると次の図のような感じだ．

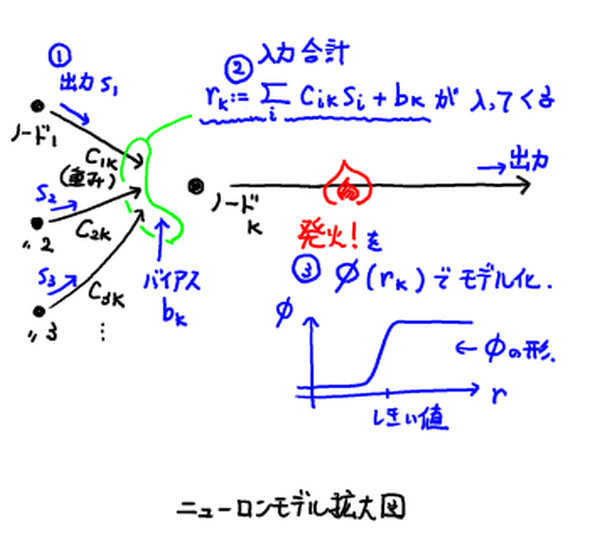
少し解説しよう．

• 信号を送ってくるノード $i$ からの信号をノード $k$ がどれだけ受け入れるかは調整パラメータである 重み係数 $C_{ik}$ として表され,
  
  
• ノード $k$ の発火のしやすさは調整パラメータである バイアス $b_k$ で表される．
  
  
• 入力信号が多いと出力信号が作られる「発火」という現象は，入力の合計を $r$ として非線形関数 $\phi(r)$ で表される． この関数のことを 活性化関数 (activation function)と呼んだりする． 活性化関数にはいくつか提案されているものが有り，典型的なのは次のようなものだ． 活性化関数を変えると NN の挙動が結構変わるので，実際に NN を使う場合はいくつか試してみると良い．
  
  
• 活性化関数の例

  名前	関数	グラフ
  シグモイド関数(sigmoid)	$\displaystyle \sigma(r) = \frac{1}{ 1 + e^{-r} }$
  tanh 関数	$\displaystyle \tanh(r) = \frac{ e^r - e^{-r} }{ e^r + e^{-r}}$
  正規化線形関数(ReLU)	$\mbox{ReLU}(r) = \max(0,r)$

そしてこのノードを集めて層を作り，その層を繋げたものが neural network だ．イメージは次のような感じになる．

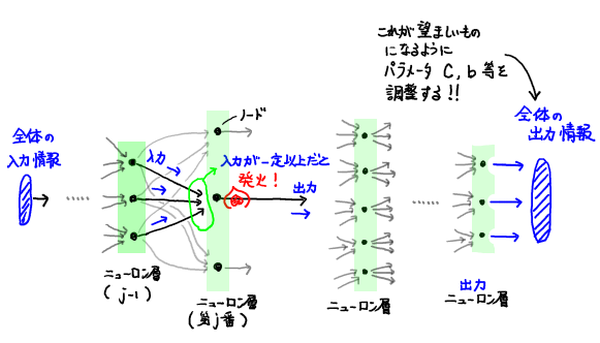図: neural network 全体のイメージ

そして，入力に対して出てくる出力が望ましいものになるべく近づくよう，パラメータ $C,b$ を調整していく(これが学習)，ということを繰り返すことでこの neural network を望ましいものへと改善していくのだ．

この調整，つまり学習をどう行うかだが，これは最小化問題という文脈の問題を解決する技術が使える． すぐ後で解説するのでそこまで待とう．

今回の最初のターゲット

機械学習の重要な本質の一つは「明示的なアルゴリズムではどうやって解決方法を実現したら良いかわからない問題」に解決方法を与えるところにある． しかしまあ，今回は最初の入門問題として，大変簡単な問題を「解決できないふりをして」取り組むことにしよう．

今回扱う問題は， $x \in [0,1]$ に対して実際は

$g(x) = \left\{\begin{array}{rcl} 1 & : & 1 / 3 < x < 2 / 3, \cr 0 & : & \mbox{ otherwise } \end{array}\right.$

である関数を，その関数形を知らない状態で データ $\{ x_k, g(x_k) \}_{k = 1}^{N_d}$ だけをもらってその情報から近似関数を作ろう，という問題としよう． もちろん，この問題は通常は「補間」技術を用いたほうが筋も結果も計算時間も良いのだが，今回は敢えて機械学習の練習問題としてこれを扱おう．

用意する neural netowrk

スカラー実数 $x$ を入力とし出力はスカラー実数であるような，大変単純な NN を今回は考えよう．

まず，NN の構造を説明しよう． NN は結構多めの「層」をつなげて，そこに現れる多数のパラメータを「学習」によってチューンすることで所望の出力を得られるようにしよう，という関数だ． その層だが，典型的には一層ずつは以下のような形をしている．

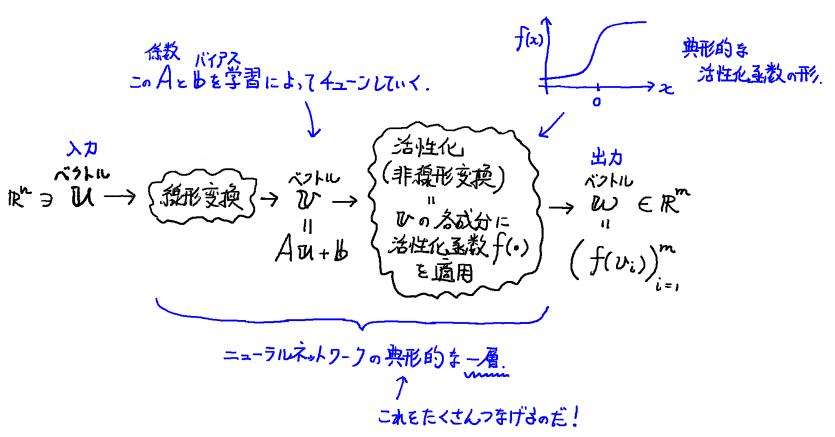
そして今回の問題では，こうしたパラメータをもつ層が 3つであるような NN を考えよう． 大雑把には下図のような設計になる．

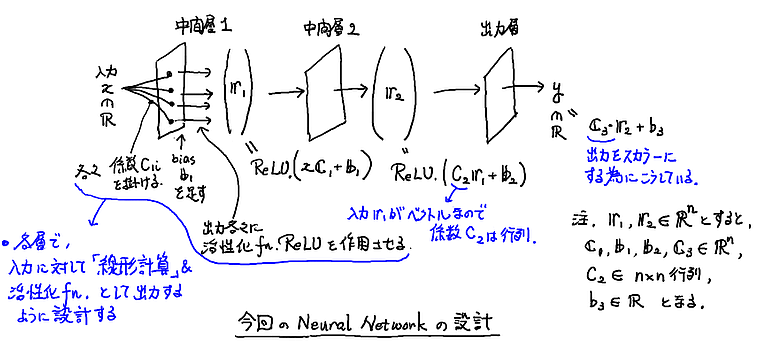
より具体的には， 入力を $x$, 出力を $y$, 中間層(ベクトル, 要素数 $n$)の出力をそれぞれ $\boldsymbol{r}^{(1)}$, $\boldsymbol{r}^{(2)}$ として， 密結合係数として $n$ 次元ベクトル $\boldsymbol{C}_1, \boldsymbol{C}_3$ と $n \times n$ 行列 $C_2$, バイアスとして $n$ 次元ベクトル $\boldsymbol{b}_1$, $\boldsymbol{b}_2$, スカラー $b_3$ を用意して，NN が

$\left\{\begin{array}{rcl} \boldsymbol{r}^{(1)} & = & \mbox{ ReLU }( x \boldsymbol{C}_1 + \boldsymbol{b}_1), \cr \boldsymbol{r}^{(2)} & = & \mbox{ ReLU }( C_2 \boldsymbol{r}^{(1)} + \boldsymbol{b}_2), \cr \mbox{ 出力 } y & = & \boldsymbol{C}_3 \cdot \boldsymbol{r}^{(2)} + b_3 . \end{array}\right.$

となっているケース(ほぼ最小限セットだな)を考える． $n$ はそうだなあ，たぶん 5 ～ 10 ぐらいでうまくいくだろう(かなり無駄が多いけどな)．

さて，関数としてこの全体を NN という名前で呼ぶことにしよう． つまり，$\mbox{output } y = \mbox{NN}( H, \mbox{ input } x)$ という感じだ．

ただし $H$ はこの NN のパラメータ $C_1 \cdots C_3$, $b_1 \cdots b_3$ を適当に一つにまとめたデータだ． 今回は，たとえば下図のようにまとめればよいだろう．

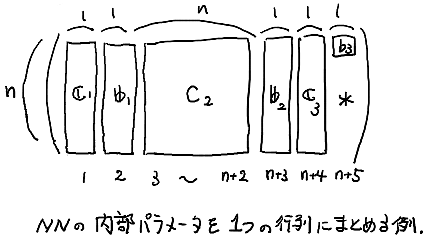
このようにパラメータを一つの量としてまとめておくことで，これらのパラメータを同時に更新して NN を「改善」する手法が使いやすくなる． 具体的には，プログラム中で gradient を利用「できる」ことがその恩恵にあたる．

NN をどう使うの？

使い方は簡単だ．

まず，既知のデータから一つ適当な $x_k$ を関数 NN に入れると値が出てくるので，これとデータに入っている $g(x_k)$ (教師情報. 出力の正解のこと)を比べて誤差 $f(H, x_k)$ を計算する． 今回の場合，$x_k$ も $g(x_k)$ もスカラーなので，誤差関数 $f$ もスカラーで正なものとして定義しておくと良いだろう．

そして，この誤差 $f(H, x_k)$ が小さくなるように NN のパラメータ $H = ($ $\boldsymbol{C}_1$, $\boldsymbol{b}_1$, $C_2$, $\boldsymbol{b}_2$, $\boldsymbol{C}_3$, $b_3$ $)$を修正するのだ！

どうやって？ と思うかもしれないが，これは「最小化問題」という情報系の古典的な問題で，いろんな技術が開発されている． 今回は一番シンプルな勾配法

$\left\{\begin{array}{rcl} H_{ \mbox{new}} & = & H + \Delta H, \cr \Delta H & = & - \gamma \, \mbox{ grad}_H \, f(H) . \end{array}\right.$

に沿ってパラメータ $H$ を改善していく手法でいこう． ただし $\gamma > 0$ はスカラーパラメータで，学習係数などと呼ばれる量に対応している．

  深層学習の発展: 何層もあるような neural network で作った関数 $f$ に対して $\mbox{ grad}_H \, f(H)$ をどうやって計算したら良いのか？ という問題には，back propagation と呼ばれる技術が「再発見」されたことである意味解決した． ちなみにこの back propagation は自動微分²と呼ばれる技術の一部で応用数学では広く知られたものなので，情報系研究者の勉強不足と指摘されてもしかたない. ただし，これだけでは「10層以上の深い層を持つ neural network」の改善がうまくいかず，しばらくこの分野の研究は停滞した．その後，特別な構造のneural network を作ったり ReLU 活性化関数を使うなどの工夫を重ねることで改善がなされて再びこの分野が脚光を浴び，現状に至っている．

さて話を戻そう． この式中の係数 $\gamma > 0$ であるが，スカラー関数 $f$ に対して数値計算的には

\[ \gamma = \frac{f(H)}{ \left\| \mbox{grad}_H f(H) \right\|^2 } \]

という感じに計算すると妥当な感じだ³． ただし，この計算式をそのまま使うと $\mbox{grad}_H f(H) \cong \boldsymbol{0}$ の時に不安定になるので， $\mbox{grad}_H f(H)$ がある程度小さい時はこの $\gamma$ を適当な数字に決めてしまうなどの対応をしておくのが良い．

そしてこの修正プロセスを，データの個数だけ繰り返せば良いんじゃね？ というのが今回の全体の大雑把な NN の使い方だ．

これでうまくいくのかって？ まあ，まずはやってみるのが一番だ．

実際にやってみる

あとは少しずつプログラムを作っていくだけだ． まず，今回 gradient を使いたいので，その機能が入っているパッケージ ForwardDiff を使うことにしよう．

このパッケージは，阪大情報教育システムやサイバーメディアセンターの JupyterHubサービス環境だと既にインストール済みだ． 個人環境で未インストールの場合は下記のようにしてインストールしておこう．

1
2

using Pkg
Pkg.add("ForwardDiff")

さて，ではパッケージの利用宣言をしてから，問題のパラメータを設定してしまおう．

1
2
3
4

using LinearAlgebra
using ForwardDiff: gradient  # 誤差の勾配を求めるのに使う

n = 10 # 中間層のサイズ．これは大変小さいほうだ．

次に、対象関数を教師情報の代わりに作ってしまおう．

1

predict(x) = round( sin(π*x)/√3 )

プロットして確認しておこう．

1
2
3
4

using Plots

X = 0:0.01:1.0
plot(X, predict)

次に，NN を作ってしまおう．gradient を計算するライブラリの都合を考慮して，(データに多少無駄が入るが)次のような感じになる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

relu(x) = (x > 0.0) ? x : 0.0 # まず ReLU を実装して，

# Neural Network. 
# 説明したとおり，パラメータをまとめて大きな行列としている.
# ここでは下記引数の M のことで，上図や全体では H のこと．
function nn(M, input) 
    C1 = view( M, :, 1 )
    b1 = view( M, :, 2 )

    C2 = view( M, :, 3:n+2 )
    b2 = view( M, :, n+3 )

    C3 = view( M, :, n+4 ) 
    b3 = M[1, n+5]         
    # 1 x 1 行列を参照すると行列のままなので，スカラーとしてコピー．

    r1 = relu.( input * C1 + b1 ) # 中間層1 出力
    r2 = relu.( C2 * r1 + b2 )    # 中間層2 出力
    r3 = dot(C3, r2) + b3    # 出力

    return r3

end

誤差の計算は，単なる(スカラー値の)差の二乗にしておこう．

1
2

# 損失関数．要は，出力の誤差．
loss(x,y) = (x - y)^2

さてそろそろ計算そのものの準備に入ろう．まずは，肝心のパラメータ群の初期値を乱数で適当に生成する．

1
2

# NN のパラメータ行列 H の初期値を乱数で生成．これを少しずつ修正する．
H = rand(n,n+5) .- 0.5

10×15 Matrix{Float64}:
0.324676  -0.317048  -0.383325  …  -0.192679     0.251531   -0.355099
0.356019  -0.24486    0.183784     -0.288493    -0.318379   -0.357167
…
-0.280295   0.465438  -0.266818      0.128114     0.0609274  -0.358294
-0.375012   0.481077  -0.357738      0.290997     0.249286   -0.0404348

このパラメータで関数 NN はどうなっているかをプロットして見ておこう．

1
2

# 最初はこんな関数が実現されている(乱数によるのでやるたびに異なる)
plot( X, x-> nn(H, x))

乱数で作っているので当たり前だけど，ターゲット関数とはまるで異なるよな．

では，肝心の計算だ！ かなり簡単だぞ．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

f(H, x) = @inbounds loss(predict(x), nn(H,x))  
# gradient の為に，出力の誤差を関数の形に書く．

using ProgressMeter

@showprogress for i in 1:200000  # 200000個のデータがある想定で．
   x = rand()  # 適当に input x を選んで(本来は集めたデータの入力値)
   output = f(H,x) # 出力のズレ. 小さくしたい．

   grad_f = @inbounds gradient(H -> f(H,x), H) 
   # 誤差の H に対する勾配

   grad_size = norm(grad_f)^2 # 勾配の大きさ

   if grad_size < 0.05 # 学習係数の調整(数字は適当)
        γ = 0.1
    else
        γ = output / grad_size
    end

    H +=  -γ * grad_f # パラメータ H を修正．
end

Progress: 100%|███████████████████████████████| Time: 0:01:31

  教師データとして関数 predict を使っているのは「ズル」と言えばずるいので，真面目にやるならデータを作っておこうw

さて, 学習がうまくいったのかどうか，学習して作り出した近似関数をグラフでチェックしよう．

1

plot( X, x-> nn(H, x))

おお? なんか微妙だが，まあうまくいったと言えるかな． なんにも考えないでループを回せばうまくいくんだから，機械学習というのは確かに「良い」方法と言えるのでは，と思うのも無理のないところだ⁴．

ちなみに，修正後のパラメータ群の数字を以下のようにして見てみると，

1

H

10×15 Matrix{Float64}:
 -0.345549   -0.0618126  -0.445271    …  -0.332966    0.331669    0.996946
 -0.0928715   0.0550843  -0.177088       -0.28505     0.281619   -0.375822
  3.18152    -0.973203    0.0805589       0.0288185  -0.482708    0.110787
 -0.163859   -0.401726   -0.195369       -0.215132    0.45405     0.0403264
 -3.54412     2.41946     0.00591301     -0.405675    0.369584    0.38548
 -0.159669   -0.109589    0.409258    …  -0.20386    -0.403797    0.0653601
 -0.900735    0.314027   -0.446676       -0.31878    -0.0162964   0.15934
  2.42244    -0.740656   -0.441479        0.655883   -1.49048    -0.440296
  0.136765   -0.13781    -0.223872        0.106524   -0.875419   -0.490622
 -0.366776   -0.198196   -0.365418        0.512018   -1.44245    -0.0656898

という感じだ． よーく見ると，たとえば $\boldsymbol{C}_1$ (上の第1列相当), $\boldsymbol{b}_1$ (上の第2列相当) は第 3, 5, 8 成分が比較的大きいので，その 3つの成分で最初の中間層の出力 $\boldsymbol{r}^{(1)}$ の性質がおおよそ見えるのではないか，などということが考察される．そのあたりを追いかけてみるのも面白いだろう．

もっと現実的な問題に適用してみよう！

この 画像ファイル は クリエイティブ・コモンズ 表示-継承 3.0 非移植ライセンス のもとに利用を許諾されています。

例えば，がく片の長さと幅，花びらの長さと幅という 4つの数字と「その花の種類(3種類: ヒオウギアヤメ, ブルーフラッグ, バージニカ)」をデータ化した UCI のアヤメのデータ をもとに，その4つの数字だけから花の種類を当てる問題を考えよう．

このデータだけではなく， UCI の Machine Learning Repository には機械学習に使えそうな多くの「データ」があるので見てみると良いだろう． ちなみにこのアヤメのデータは現時点だと「最も人気のある」ものだね．

上のアヤメのデータだが，直接自分でファイルをダウンロードしてそのファイルを読み込む形で Julia に入力してもよいが，これは有名なデータなので RDatasets や MLDatasets ⁵といったいろいろなパッケージがこのデータを自動でダウンロードしてくれる． 今回は下記に示すように， MLDatasets パッケージを用いて読み込もう．

なお，データの使い方等は MLDatasets.jl/Iris を見ると，このアヤメ(iris)のデータをどう使えばよいかが書いてある．

この MLDatasets パッケージだが，阪大情報教育システムやサイバーメディアセンターの JupyterHubサービス環境ではやはり既にインストール済みだ． 個人環境で未インストールの場合は下記のようにしてインストールしておこう．

1
2

using Pkg
Pkg.add("MLDatasets")

それから，データ処理ライブラリ DataFrames, 機械学習フレームワークである Flux パッケージの機能も一部使うことにしよう． これらも阪大情報教育システムやサイバーメディアセンターの JupyterHubサービス環境ではやはり既にインストール済みだ． 個人環境で未インストールの場合は下記のようにしてインストールしておこう．

1
2
3

using Pkg
Pkg.add("DataFrames")
Pkg.add("Flux")

さて，あらためて話を戻そう．まず，使いそうなパッケージの利用宣言だ．

1
2
3
4
5
6
7

using LinearAlgebra
using DataFrames
using Flux 
# Flux にも gradient (同じ機能)があるので ForwardDiff は不要．
using MLDatasets
using Statistics
using ProgressMeter

そして，アヤメのデータを使わせていただこう． それには関数 Iris を呼び出せばよい．

ただし，この関数を初めて呼び出したときにデータが(一回だけ)ダウンロードされるので解説しよう． 実際は，下記のように，このデータについてごく簡単な説明があり，それを理解した上でダウンロードするのか，y/n で尋ねられる． そこで stdin> に "y" (と Enter)を入力しよう． するとダウンロードが始まる．少しだけ待とう．

1

Iris()

stdin> ■■■■■■

This program has requested access to the data dependency Iris.
which is not currently installed. It can be installed automatically, and you will not see this message again.

Dataset: The Iris dataset
Website: https://archive.ics.uci.edu/ml/datasets/Iris

Do you want to download the dataset from ["https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"] to "/usr/local/julia/share/julia/datadeps/Iris"?
[y/n]

すると，次のようにダウンロード結果が表示される. なお，よく見ると分かるように，データはデフォルトでは DataFrame 形式で格納される．

dataset Iris:
  metadata   =>    Dict{String, Any} with 4 entries
  features   =>    150×4 DataFrame
  targets    =>    150×1 DataFrame
  dataframe  =>    150×5 DataFrame

あとはこのデータを使うだけだ． まず，菖蒲の 4つの特徴データと，花の名前データを以下のようにして配列に入れよう．

1
2
3

features_raw = Matrix( Iris().features )
labels_raw   = Matrix( Iris().targets )
#  花の4つの数字情報と，花の種類を配列に入れる．

150×1 Matrix{InlineStrings.String15}:
 "Iris-setosa"
 "Iris-setosa"
 "Iris-setosa"
 ⋮
 "Iris-virginica"
 "Iris-virginica"
 "Iris-virginica"

features_raw[i,:] に i番目の花の 4つの数字データが入り，labels_raw[i] にそのアヤメの種類が入るという格好だ．

  上のデータから想像はつくと思うが，データ 150個のうち， 最初の 50個が "Iris-setosa"(ヒオウギアヤメ), 次の 50個が "Iris-versicolor"(ブルーフラッグ), 最後の 50個が "Iris-verginica"(バージニカ) のデータだ． そのつもりでこれからのプログラムを読んでいこう．

データの軽い事前チェック

とりあえずこれらのデータで花の種類を分類できそうかどうか，次のようにしてちょっとグラフで見てみよう． ただし，われわれは３次元グラフまでしか理解できないので，とりあえず 3つの数字(がくの長さ，幅，花びらの長さ)でプロットしてみる．

まず，面倒だが，データを花の種類ごとに分けてみる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

X1 = features_raw[1:50, 1]
Y1 = features_raw[1:50, 2]
Z1 = features_raw[1:50, 3]
W1 = features_raw[1:50, 4]

X2 = features_raw[51:100, 1]
Y2 = features_raw[51:100, 2]
Z2 = features_raw[51:100, 3]
W2 = features_raw[51:100, 4]

X3 = features_raw[101:150, 1]
Y3 = features_raw[101:150, 2]
Z3 = features_raw[101:150, 3]
W3 = features_raw[101:150, 4]

そしてこれを以下のようにプロットしてみよう．

1
2
3
4
5
6
7

using Plots

default( markersize = 4, camera = (30,15))

scatter(  X1, Y1, Z1, xaxis=("sepal length (cm)"), yaxis=("sepal width (cm)"), zaxis=("petal length (cm)"), label = "Iris setosa" )
scatter!( X2, Y2, Z2, label = "Iris versicolor" )
scatter!( X3, Y3, Z3, label = "Iris virginica" )

ふむ，目で見ても結構別れているので，NN に学習させてもうまくいくと期待して良さそうな気がするね．

話を戻そう

アヤメの種類が文字列のままだと使いにくいので，次の形に変換しておこう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13

# 名前をもらって，どの分類かに書き換える関数．
function RawToNum(str)
    if str == "Iris-setosa"
        return [ 1.0, 0, 0 ]
    elseif str == "Iris-versicolor"
        return [ 0, 1.0, 0 ]
    else
        return [ 0, 0, 1.0 ]
    end
end

# この labels にベクトルの形で分類データが入る．
labels = RawToNum.(labels_raw)

150×1 Matrix{Vector{Float64}}:
 [1.0, 0.0, 0.0]
 [1.0, 0.0, 0.0]
 [1.0, 0.0, 0.0]
 ⋮
 [0.0, 0.0, 1.0]
 [0.0, 0.0, 1.0]
 [0.0, 0.0, 1.0]

なぜこんな形で分類結果を表記するのかは，NN の出力と合わせるためだ．あとでわかってくるだろうからこの時点ではあまり気にしなくて良い．

さて次に，このデータのうち一部を「学習後の NN の能力チェック用」に分離してとっておき，それには NN の学習が済むまで参照しないようにしよう． 全部でたった 150個しかデータがないのでもったいないが，これを別にしておかないと能力チェックが困難になってしまう．

1
2
3
4
5
6

# 学習後のチェックに使うデータをとっておく．学習には用いない．
# 3種類の花のデータを5個ずつ，チェック用に抜き出しておく．

toCheckIDs = vcat( 46:50, 96:100, 146:150 )  
features_raw_toCheck = features_raw[ toCheckIDs, : ]
labels_toCheck = labels[toCheckIDs]

15-element Vector{Vector{Float64}}:
 [1.0, 0.0, 0.0]
 [1.0, 0.0, 0.0]
 ⋮

残りは学習に使えるデータだ．

1
2
3
4
5

# 学習に使うデータ．

SampleIDs = setdiff( 1:150, toCheckIDs )
features_raw_sample = features_raw[ SampleIDs, : ]
labels_sample = labels[SampleIDs]

135-element Vector{Vector{Float64}}:
 [1.0, 0.0, 0.0]
 [1.0, 0.0, 0.0]
 ⋮

次に，花のがく片の長さ…等の数字を正規化しよう． それぞれの数字の大きさ等が異なるのに NN で混ぜるのは NN の性能を下げるだけなので，こうしておこう．

1
2
3
4
5
6
7
8

# 入力データの数字的な偏りをなるべくなくしておく．
# ただし，事前に使える平均，偏差はサンプル値からしかとれない.

Std = [ std( features_raw_sample[ :, i ] ) for i in 1:4 ]'
Mean = [ mean( features_raw_sample[ :, i ] ) for i in 1:4 ]'

features_toCheck = (features_raw_toCheck .- Mean) ./ Std
features_sample  = (features_raw_sample  .- Mean) ./ Std

さて，肝心の NN そのものを定義しよう． 先の例題よりずっと難しいはずの問題だから，少し n を大きくし，また 中間層も増やそう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

# NN の定義．少し層を増やした．まあこれでも小さい方だな．

n = 20

function nn(M, input) 
    Ci = view( M, :, 1:4 )
    bi = view( M, :, 5 )

    C1 = view( M, :, 6:n+5 )
    b1 = view( M, :, n+6 )

    C2 = view( M, :, n+7:2n+6 )
    b2 = view( M, :, 2n+7 )

    C3 = view( M, :, 2n+8:3n+7 )
    b3 = view( M, :, 3n+8 )

    C4 = view( M, :, 3n+9:4n+8 )
    b4 = view( M, :, 4n+9 )

    C5 = view( M, :, 4n+10:5n+9 )
    b5 = view( M, :, 5n+10 )

    Co = ( view( M, :, 5n+11:5n+13 ) )' # 転置
    bo = view( M, 1:3, 5n+14 )

    r1 =  sigmoid.( Ci * input + bi ) # 入力値処理

    r2 = sigmoid.( C1 * r1 + b1 ) 
    r3 = sigmoid.( C2 * r2 + b2 ) # 中間層．ReLU や TanhShrink だとうまくいかない．
    r4 = sigmoid.( C3 * r3 + b3 )
    r5 = sigmoid.( C4 * r4 + b4 )
    r6 = sigmoid.( C5 * r5 + b5 )

    output = softmax( Co * r6 + bo ) # 出力値処理

    return output
end

ちなみに，この NN の出力直前の softmax 関数というのは実数の列(負の実数もOK)を確率分布として解釈できる数列に(かつ，各要素は単調に)変換する関数の一つで，ベクトル $\boldsymbol{a} = \{ a_i \}$ に対して

$\displaystyle\mbox{ SoftMax }(\boldsymbol{a})_i = \frac{\exp(a_i)}{\sum_i \exp(a_i)}$

と定義できる． まあ，$\exp$ 関数で強引に正の値に変換してから合計値で正規化しているという，シンプルな変換だ． 単調性と確率分布の性質を満たそうとするとたぶんこれが最初の候補だろう． ちなみに，すべての $a_i$ が正ならば， $\exp$ での変換が不要で，合計値で割って単純に正規化したほうが楽だろうな．

あとは誤差(損失関数)を定義し，パラメータの初期値を用意すれば良い．

1
2
3
4
5
6

# 結果の誤差は，分類問題での定番である crossentropy にて．
loss( output, v_true ) = Flux.crossentropy( output, v_true )
g(H, i) = loss( nn(H, features_sample[i, :]), labels_sample[i] ) 

# NN のパラメータ行列 H の初期値を乱数で生成．これを少しずつ修正する．
H = 10.0 * ( rand(n,5n+14) .- 0.5 )

20×114 Matrix{Float64}:
 -1.75717   -2.00612   -0.796069   …   3.58165     1.02768    -3.26719
  4.74954   -0.491002   3.0711         2.21145    -3.16719    -0.0425997
  2.02711    2.17022    4.51241       -0.589745    4.25787     1.35962
  2.51323    0.107898   2.80897       -1.28247     4.33434     4.85903
…
 -2.53355    2.31796    2.15024        4.03668     1.01585    -3.40334
 -3.74638    2.94393    4.83269        4.92261     2.97446     2.97175
 -4.97509    4.79206    3.46386        1.21201     4.73185    -0.971052
  0.599212  -1.4483    -1.61121       -2.99346    -2.14352     0.430389

ちなみに，誤差を測る方法として出力ベクトル $\boldsymbol{y}$ と真値ベクトル $\boldsymbol{z}$ に対する Cross Entropy

$\displaystyle\mbox{ CrossEntropy }(\boldsymbol{y}, \boldsymbol{z}) = - \sum_i \, z_i \, \log( y_i )$

を使っている． これは情報幾何学と呼ばれる分野で確率分布間の擬似的な「距離もどき」として使われる Kullback-Leibler divergence と $\mathbf{z}$ のエントロピー分がズレただけの量なので， まあ，確率分布関数 $\mathbf{y}$ と $\mathbf{z}$ の距離もどきとして使える量だ，と思っていいだろう．

さて，あとは少し強引だが，下記のように学習させてしまおう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22

# NN の学習
itr = 500
datasize = size(labels_sample)[1]

@showprogress for i in 1:(itr * datasize)
    
   num = rand(1:datasize) # データの順序に依存しないように乱数で

   grad_f = Flux.gradient(M -> g(M, num), H)[1] 
   # 誤差の H に対する勾配. 
   # 今回は Flux の gradient を使う(機能は同じ．こちらは最後に [1] をつけて結果を取り出すところが違う)

   grad_size = norm(grad_f)^2 # 勾配の大きさ

   if grad_size < 0.01 # 学習係数の調整(数字は適当)
        γ = 0.1
    else
        γ = g(H,num) / grad_size
    end

    H +=  -γ * grad_f # パラメータ H を修正．
end

Progress: 100%|███████████████████████████████| Time: 0:00:36

うまく学習できたか，少し見てみよう． まずはサンプルデータの1番目だ．

1
2
3
4

# チェックのための簡易表記
nn_sample(i) = nn( H, features_sample[i,:] )

nn_sample(1)

3-element Vector{Float64}:
 0.9998718073031901
 0.00011342262609513533
 1.4770070714572282e-5

この出力は，まあ，NN がどの分類であるかの確率出力を出した，と思えば良い． だからこの場合は 1種類目のアヤメの確率が高いと言っているわけで，実際は

1

labels_sample[1]

3-element Vector{Float64}:
 1.0
 0.0
 0.0

より，実際もそうであることがわかる．

あと 2点ほど手動でチェックしてみよう．次に，2種類目のアヤメのデータであるはずの 70番目のデータに対する NN の出力を見ると，

1

nn_sample(70)

3-element Vector{Float64}:
 0.00011953500611063386
 0.999791436680806
 8.902831308321433e-5

となっており，やはりこの場合も正しく学習できていることがわかる．

同様に，3種類目のアヤメのデータである 130番目のデータを NN に入力すると，

1

nn_sample(130)

3-element Vector{Float64}:
 1.566249199174758e-5
 7.54571785895798e-5
 0.9999088803294187

となり，このデータに対してもやはり正しく学習できていることが確認できる．

実際，この場合はすべて正しく学習できていて(初期値が乱数によるので，もちろん人によって異なりうるが), 次のように確かめられる． まず，NN の確率出力をもらってどう判断するか，という操作を次のような関数にしよう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

# 出力値による判断を明確にする関数
function decision(x)
  v = similar(x)
  max_i = argmax(x)

  for i in 1:size(x)[1]
    if i == max_i
      v[i] = 1.0
    else
      v[i] = 0.0
    end
  end

  return v
end

こうしておいて，学習に使ったサンプルデータと，NN の出力による判断値の違いを次のようにまとめる．

1

error_sample = labels_sample - decision.( nn_sample.(1:135) )

135-element Vector{Vector{Float64}}:
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 ⋮
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]

画面で見える限りのケースでは学習はうまくいっているように見える．一つもミスがないか確かめておこう．

1

sum( norm.(error_sample) )

0.0

うむ，学習に使ったデータに対しては 100% の学習ができたことがこれで確認できた．

では，肝心の，「初めてみるデータに対して確かに NN は判断ができるか」をチェックしよう． まずは手動でいくつか確認してみよう．

1
2
3
4

# 初めて見るデータに対しての NN の判断
nn_toCheck(i) = nn( H, features_toCheck[i,:])

nn_toCheck(1)

3-element Vector{Float64}:
 0.9998635385590626
 0.0001237852949814865
 1.267614595568828e-5

ふむ，これは本来の 46番目のデータ(花は一種類目)に対する NN の判断だが，確かに正しい．

ほかも見てみよう．

1

nn_toCheck(6)

3-element Vector{Float64}:
 0.00013408530146803477
 0.9997878607306641
 7.80539678678173e-5

そしてこれは本来の 96番目のデータ(花は二種類目)に対する NN の判断だ. これも確かに正しい．

次はどうかな．

1

nn_toCheck(11)

3-element Vector{Float64}:
 1.9082514255861888e-5
 6.692681398232692e-5
 0.9999139906717618

これは本来の 146番目のデータ(花は三種類目)に対する NN の判断で，これも確かに正しいな．

NN が知らない15個のデータに対して一気にチェックしよう．

1

error_toCheck = labels_toCheck - decision.( nn_toCheck.(1:15) )

15-element Vector{Vector{Float64}}:
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]

おお. 一箇所もミスが無い．すべてうまくいったな． まあたまたまではあるはずだが，未知のデータに対して，100% の正解率だな． こんな簡単な作りの NN に 135個のデータを与えて学習させることでこの判断正解率なので，なかなか良いと考えて良さそうだ． もっとたくさんデータが与えて学習させれば，確実に高い正解率になるのだろうと期待できる．

というわけで，今回は十分に良い機械学習ができたと言えよう． ただし，過学習(過学習についてはレポートにて)の恐れはあるのでそこは調べておいて，機械学習の現場では忘れないようにしよう．

レポート

下記要領でレポートを出してみよう．

• e-mail にて，
• 題名を 2022-numerical-analysis-report-12 として,
• 教官宛(アドレスは web の "TOP" を見よう)に，
• 自分の学籍番号と名前を必ず書き込んで，
• 内容はテキストでも良いし，pdf などの電子ファイルを添付しても良いので，

下記の内容を実行して，結果や解析，感想等をレポートとして提出しよう．

1. 最初のターゲット問題の2次元バージョンに取り組んでみよう．
   
   具体的には，図
   の中で定義される関数 $S_c$ に従ってデータ $D = \{ \boldsymbol{x}_k, \boldsymbol{y}_k = S_c(\boldsymbol{x}_k) \}_{k=1}^N$ が $N \cong 10,000$ 程度で得られているとする($N$ は好きに設定して良い)．
   
   関数 $S_c$ が未知である想定のもとに，今回の授業と同様に NN を構成し，データ $D$ を使ってパラメータを学習させて，NN が関数 $S_c$ を近似的に構成するようにしてみよう．
   
   注: この問題は，2つのパラメータ( $\Omega$ 上の座標 $(x,y)$ のこと)から 2種類の分類(0 か 1 か)ができるように，という機械学習を行うことに相当する．
   
   
2. 「過学習」について，文献などを用いて調べ，自分なりに対応策を考えてみよう．考えた対応策がうまくいくかは，細かい工夫によって随分変わったりするので，ここではそこまで実現可能性や効率等についてあまり考えなくて良い．