15. 機械学習入門 • Daisuke Furihata (降籏大介)

機械学習入門

最後にせっかくなので，近年たいへんに発達し注目されている機械学習について簡単に学んでおこう．機械学習を行う道具立てとしては今回は前回学んだ Julia を素で使い，機械学習用のライブラリ・フレームワーク等は無しという状況でやってみることにしよう．

Neural network と深層学習

機械学習という分野は広くて様々な技術を含むが，最近注目されているのは neural network (NN と略されることも多い) と呼ばれる「関数」を用いた深層学習だろう．この技術によって画像分類問題で大変画期的な結果が出て以来，大変 hot な分野であることは間違いない．

しかし，その開発が大変勢いある分野であるため，細かい技術論にまどわされて「全体がよくわからない」という者も多いだろう．

そこで今回は，その「基本的な考え方」を授業時に簡単に解説し，そして実際に自分でプログラムして動かしてみよう．

今回の最初のターゲット

機械学習の重要な本質の一つは「明示的なアルゴリズムではどうやって解決方法を実現したら良いかわからない問題」に解決方法を与えるところにある．しかしまあ，本当にそうした問題は扱いそのものがそれなりに面倒だったりするので，今回は入門として，大変簡単な問題を「解決できないふりをして」取り組むターゲットとして扱おう．

今回扱う問題は， $x \in [0,1]$ に対して実際は

$g(x) = \left\{\begin{array}{rcl} 1 & : & 1 / 3 < x < 2 / 3, \cr 0 & : & \mbox{ otherwise } \end{array}\right.$

である関数を，その関数形を知らない状態で データ $\{ x_k, g(x_k) \}_{k = 1}^{N_d}$ だけをもらってその情報から近似関数を作ろう，という問題としよう．もちろん，この問題は通常は「補間」技術を用いたほうが筋も結果も計算時間も良いのだが，今回は敢えて機械学習の練習問題としてこれを扱おう．

用意する neural netowrk

スカラー実数 $x$ を入力とし出力はスカラー実数であるような，大変単純な NN を今回は考えよう．

まず，NN の構造を説明しよう． NN は結構多めの「層」をつなげて，そこに現れる多数のパラメータを「学習」によってチューンすることで所望の出力を得られるようにしよう，という関数だ．その層だが，典型的には一層ずつは以下のような形をしている．

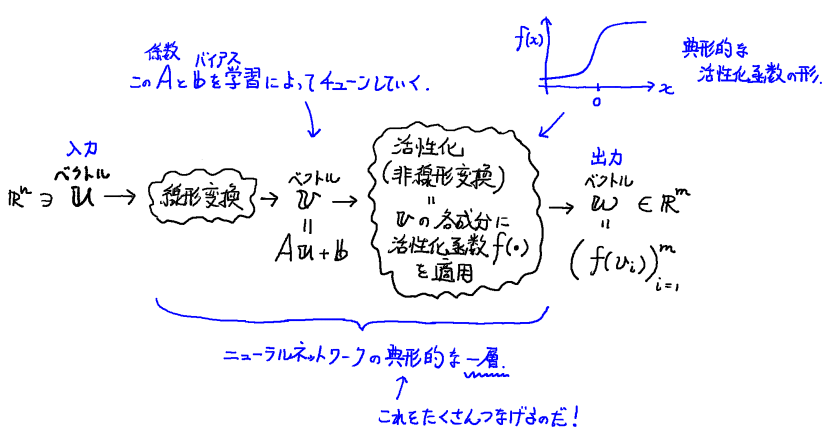
そして今回の問題では，こうしたパラメータをもつ層が 3つであるような NN を考えよう．大雑把には下図のような設計になるかな．

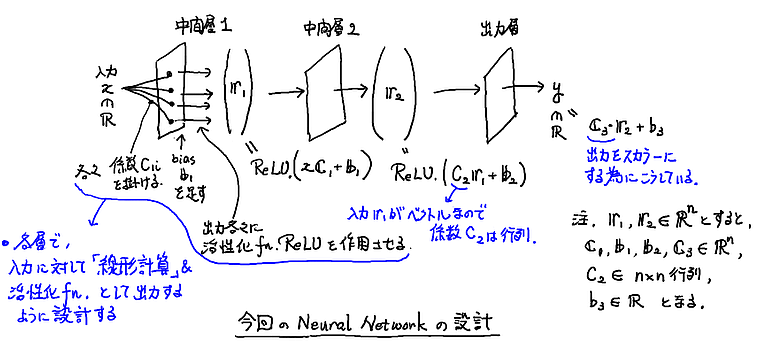
より具体的には，入力を $x$, 出力を $y$, 中間層(ベクトル, 要素数 $n$)の出力をそれぞれ $\boldsymbol{r}^{(1)}$, $\boldsymbol{r}^{(2)}$ として，密結合係数として $n$ 次元ベクトル $\boldsymbol{C}_1, \boldsymbol{C}_3$ と $n \times n$ 行列 $C_2$, バイアスとして $n$ 次元ベクトル $\boldsymbol{b}_1$, $\boldsymbol{b}_2$, スカラー $b_3$ を用意して，NN が

$\left\{\begin{array}{rcl} \boldsymbol{r}^{(1)} & = & \mbox{ ReLU }( x \boldsymbol{C}_1 + \boldsymbol{b}_1), \cr \boldsymbol{r}^{(2)} & = & \mbox{ ReLU }( C_2 \boldsymbol{r}^{(1)} + \boldsymbol{b}_2), \cr \mbox{ 出力 } y & = & \boldsymbol{C}_3 \cdot \boldsymbol{r}^{(2)} + b_3 . \end{array}\right.$

となっているケース(ほぼ最小限セットだな)を考える． $n$ はそうだなあ，たぶん 5 ～ 10 ぐらいでうまくいくだろう(かなり無駄が多いけどな)．

ここで出てくる ReLU 関数は活性化関数と呼ばれる関数の一つで次のように定義され，まあ，なんというか，アナログ性を消さないようにしてある if 文の役目を持つ関数と思って良い．

$\mbox{ ReLU } (x) = \left\{\begin{array}{rcl} 0 & : & x < 0, \cr x & : & 0 \leq x . \end{array}\right.$

さて，関数としてこの全体を NN という名前で呼ぶことにしよう．つまり，$\mbox{output } y = \mbox{NN}( H, \mbox{ input } x)$ という感じだ．

ただし $H$ はこの NN のパラメータ $C_1 \cdots C_3$, $b_1 \cdots b_3$ を適当に一つにまとめたデータだ．今回は，たとえば下図のようにまとめればよいだろう．

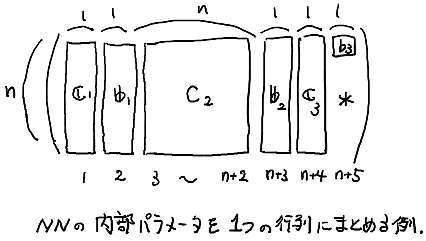
このようにパラメータを一つの量としてまとめておくことで，これらのパラメータを同時に更新して NN を「改善」する手法が使いやすくなる．具体的には，プログラム中で gradient を利用「できる」ことがその恩恵にあたる．

NN をどう使うの？

使い方は簡単だ．

まず，既知のデータから一つ適当な $x_k$ を関数 NN に入れると値が出てくるので，これとデータに入っている $g(x_k)$ (教師情報. 出力の正解のこと)を比べて誤差 $f(H, x_k)$ を計算する．今回の場合，$x_k$ も $g(x_k)$ もスカラーなので，誤差関数 $f$ もスカラーで正なものとして定義しておくと良いだろう．

そして，この誤差 $f(H, x_k)$ が小さくなるように NN のパラメータ $H = ($ $\boldsymbol{C}_1$, $\boldsymbol{b}_1$, $C_2$, $\boldsymbol{b}_2$, $\boldsymbol{C}_3$, $b_3$ $)$を修正するのだ！

どうやって？と思うかもしれないが，これは「最小化問題」とか「最適化問題」とよばれる情報系の古典的な問題で，いろんな技術が開発されている．今回は一番シンプルな勾配法

$\left\{\begin{array}{rcl} H_{ \mbox{new}} & = & H + \Delta H, \cr \Delta H & = & - \gamma \, \mbox{ grad}_H \, f(H) . \end{array}\right.$

を用いよう．ちなみにこの式中の $\gamma > 0$ は深層学習での学習係数¹と呼ばれるパラメータに対応していて，今回はスカラー関数 $f$ をゼロにすべく狙っていくわけだから数値計算的には

$\gamma = f(H) / \left\| \mbox{grad}_H f(H) \right\|^2 $

という感じに計算すると妥当な感じだ．ただし，この計算式をそのまま使うと $\mbox{grad}_H f(H) \cong \boldsymbol{0}$ の時に不安定になるので， $\mbox{grad}_H f(H)$ がある程度小さい時はこの $\gamma$ を適当な数字に決めてしまうなどの対応をしておくと良い．

そしてこの修正プロセスを，データの個数だけ繰り返せば良いんじゃね？というのが今回の全体の大雑把な NN の使い方だ．

これでうまくいくのかって？まあ，まずはやってみるのが一番だ．

実際にやってみる

あとは少しずつプログラムを作っていくだけだ．まず，今回いくつかのパッケージの機能を使いたいので(例えばパッケージ ForwardDiff の gradient など), 以下のようにしてそうしたパッケージをインストールしておこう．

1
2
3
4


using Pkg
Pkg.add("ForwardDiff")
Pkg.add("Plots")
Pkg.add("ProgressMeter")

Plots あたりがまあまあな大きさのライブラリなので，このインストール作業は少し待たされる．コーヒーでもいれよう．幸い，このインストール作業は一回だけやっておけば良い．

次に、パッケージの利用宣言と，問題のパラメータを設定してしまおう．

1
2
3
4


using LinearAlgebra
using ForwardDiff: gradient  # 誤差の勾配を求めるのに使う

n = 10 # 中間層のサイズ．これは大変小さいほうだ．

次に、対象関数を教師情報の代わりに作ってしまおう．

1

predict(x) = round( sin(π*x)/√3 )

上の式を見れば推測できるだろうが，Julia では円周率 $\pi$ や平方根計算の $\sqrt{}$ など，数学的な定数や関数，そして特殊な文字も，そう入力するだけでそのまま使えるものが多い．ちなみに, そうしたものを入力する方法は「TeXと同じ入力(バックスラッシュのあとに入力ってやつね)をしてその入力の上で Tabキーを押す」というものだ．たとえば $\alpha$ を入力したければ，\alpha と入力してそこで Tabキーを押すという感じだ．

プロットして確認しておこう．

1
2
3
4


using Plots

X = 0:0.01:1.0  # 0から1まで 0.1刻みの数字で作る「範囲」
plot(X, x-> predict(x))

target

次に，NN を作ってしまおう．gradient を計算するライブラリの都合を考慮して，(データに多少無駄が入るが)次のような感じになる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


relu(x) = (x > 0.0) ? x : 0.0 # まず ReLU を実装して，

# Neural Network. 
# 説明したとおり，パラメータをまとめて大きな行列としている.
# ここでは下記引数の M のことで，上図や全体では H のこと．
function nn(M, input) 
    C1 = view( M, :, 1 )
    b1 = view( M, :, 2 )

    C2 = view( M, :, 3:n+2 )
    b2 = view( M, :, n+3 )

    C3 = view( M, :, n+4 ) 
    b3 = M[1, n+5]         
    # 1 x 1 行列を参照すると行列のままなので，スカラーとしてコピー．

    r1 = relu.( input * C1 + b1 ) # 中間層1 出力
    r2 = relu.( C2 * r1 + b2 )    # 中間層2 出力
    r3 = dot(C3, r2) + b3    # 出力

    return r3

end

誤差の計算は，単なる(スカラー値の)差の二乗にしておこう．

1
2


# 損失関数．要は，出力の誤差．
loss(x,y) = (x - y)^2

さてそろそろ計算そのものの準備に入ろう．まずは，肝心のパラメータ群の初期値を乱数で適当に生成する．

1
2


# NN のパラメータ行列 H の初期値を乱数で生成．これを少しずつ修正する．
H = rand(n,n+5) .- 0.5

10×15 Array{Float64,2}:
0.324676  -0.317048  -0.383325  …  -0.192679     0.251531   -0.355099
0.356019  -0.24486    0.183784     -0.288493    -0.318379   -0.357167
…
-0.280295   0.465438  -0.266818      0.128114     0.0609274  -0.358294
-0.375012   0.481077  -0.357738      0.290997     0.249286   -0.0404348

このパラメータで関数 NN はどうなっているかをプロットして見ておこう．

1
2


# 最初はこんな関数が実現されている(乱数によるのでやるたびに異なる)
plot( X, x-> nn(H, x))

initial nn

乱数で作っているので当たり前だけど，ターゲット関数とはまるで異なるよな．

では，肝心の計算だ！かなり簡単だぞ．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


f(H, x) = @inbounds loss(predict(x), nn(H,x))  
# gradient の為に，出力の誤差を関数の形に書く．

using ProgressMeter

@showprogress for i in 1:200000  # 200000個のデータがある想定で．
   x = rand()  # 適当に input x を選んで(本来は集めたデータの入力値)

   grad_f = @inbounds gradient(H -> f(H,x), H) 
   # 誤差の H に対する勾配

   grad_size = norm(grad_f)^2 # 勾配の大きさ

   if grad_size < 0.05 # 学習係数の調整(数字は適当)
        γ = 0.1
    else
        γ = f(H,x) / grad_size
    end

    H +=  -γ * grad_f # パラメータ H を修正．
end

Progress: 100%|███████████████████████████████| Time: 0:00:57

今回のように学習係数 $\gamma$ を自動調整すると全体の計算がまあまあ速いかな.

ちなみに，教師データとして関数 predict を使っているのは「ズル」と言えばずるいので，真面目にやるならデータを作っておこうw

さて, 学習がうまくいったのかどうか，学習して作り出した近似関数をグラフでチェックしよう．

1

plot( X, x-> nn(H, x))

final nn

おお！なんかうまくいったことがわかる．なんにも考えないでループを回せばうまくいくんだから，機械学習というのは確かに「良い」方法と言えるのでは，と思うのも無理のないところだ²．

ちなみに，修正後のパラメータ群の数字を以下のようにして見てみると，

1

H

10×15 Array{Float64,2}:
  3.2782     -2.10464    -0.400671   -0.386785   …   0.00958044   0.000831323
 -0.0298654  -0.0267683  -0.808059   -0.0653339      0.894813    -0.151152
 -1.16015     0.406917    0.956639   -0.359122      -0.00108768  -0.259304
 -0.203468    0.0711579   0.397862   -0.242374       0.35942      0.0896417
  0.229885   -0.354939    0.268831   -0.226491      -0.308383    -0.35167
  0.209952   -0.314071    0.595492   -0.262543   …   0.635284     0.0683405
 -0.480897   -0.253232    0.0360848   0.0496048     -0.129339     0.410387
 -0.0486835  -0.303086   -2.59438     0.420436       2.81208     -0.322807
 -0.168708   -0.293341   -0.0640921   0.416565       0.0905584   -0.177777
 -3.47757     1.21767     0.681591   -0.480172      -0.552944    -0.0488756

という感じだ．

この例だと，よーく見るとたとえば $\boldsymbol{C}_1$ (上の第1列相当), $\boldsymbol{b}_1$ (上の第2列相当) は第 1, 3, 10 成分が比較的大きいので，その 3つの成分で最初の中間層の出力 $\boldsymbol{r}^{(1)}$ の性質がおおよそ見えるのではないか，などということが考察される．そのあたりを追いかけてみるのも面白いだろう．

現実の問題にこの考え方を使えないか，検討してみよう．

この画像ファイルはクリエイティブ・コモンズ表示-継承 3.0 非移植ライセンスのもとに利用を許諾されています。

例えば，がく片の長さと幅，花びらの長さと幅(いずれも cm で)という 4つの数字と「その花の種類(3種類: ヒオウギアヤメ, ブルーフラッグ, バージニカ)」をデータ化した ICU のアヤメのデータをもとに，その4つの数字だけから花の種類を当てられるようにできるだろうか．考えてみよう．

上のアヤメのデータだが，直接自分でファイルをダウンロードしてそのファイルを読み込む形で Julia に入力してもよいが，これは有名なデータなので RDatasets や MLDatasets ³といったいろいろなパッケージがこのデータを自動でダウンロードしてくれる．今回は下記に示すように， MLDatasets パッケージをインストールしてそこから読み込もう．

なお，データの使い方等は MLDatasets.jl/Iris を見ると，このアヤメ(iris)のデータをどう使えばよいかが書いてある．

まず，MLDatasets パッケージをインストールしていない人はインストールしよう．

1
2


using Pkg
Pkg.add("MLDatasets")

それから，機械学習フレームワークである Flux パッケージもインストールしよう．この中にある関数をいくつか使うのだ．

1

Pkg.add("Flux")

次に，使いそうなパッケージの利用宣言だ．

1
2
3
4
5
6


using LinearAlgebra
using Flux 
# Flux にも gradient (同じもの)があるので ForwardDiff は不要．
using MLDatasets
using Statistics
using ProgressMeter

そして，アヤメのデータを読み込もう．

1
2
3
4
5
6
7


MLDatasets.Iris.download(; i_accept_the_terms_of_use = true)
# 利用許諾条件(Creative Commons License v4)に承諾して
# 利用データをダウンロード．一回だけダウンロードすれば良い．

features_raw = MLDatasets.Iris.features()
labels_raw   = MLDatasets.Iris.labels()
#  花の4つの数字情報と，花の種類を配列に入れる．

150-element Array{String,1}:
 "Iris-setosa"
 "Iris-setosa"
 "Iris-setosa"
 ⋮
 "Iris-virginica"
 "Iris-virginica"
 "Iris-virginica"

features_raw[i] に i番目の花の 4つの数字データが入り，labels_raw[i] にそのアヤメの種類が入るという格好だ．

データの軽い事前チェック

とりあえずこれらのデータで花の種類を分類できそうかどうか，次のようにしてちょっとグラフで見てみよう．ただし，われわれは３次元グラフまでしか理解できないので，とりあえず 3つの数字(がくの長さ，幅，花びらの長さ)でプロットしてみる．

まず，面倒だが，データを花の種類ごとに分けてみる．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14


X1 = features_raw[1, 1:50]
Y1 = features_raw[2, 1:50]
Z1 = features_raw[3, 1:50]
W1 = features_raw[4, 1:50]

X2 = features_raw[1, 51:100]
Y2 = features_raw[2, 51:100]
Z2 = features_raw[3, 51:100]
W2 = features_raw[4, 51:100]

X3 = features_raw[1, 101:150]
Y3 = features_raw[2, 101:150]
Z3 = features_raw[3, 101:150]
W3 = features_raw[4, 101:150]

そしてこれを以下のようにプロットしてみよう．

1
2
3
4
5
6
7


using Plots

default( markersize = 4 )

scatter(  X1, Y1, Z1, xaxis=("sepal length (cm)"), yaxis=("sepal width (cm)"), zaxis=("petal length (cm)"), label = "Iris setosa" )
scatter!( X2, Y2, Z2, label = "Iris versicolor" )
scatter!( X3, Y3, Z3, label = "Iris virginica" )

ふむ，目で見ても結構別れているので，NN に学習させてもうまくいくと期待して良さそうな気がするね．

話を戻そう

さて話を戻して，アヤメの種類が文字列のままだと使いにくいので，次の形に変換しておこう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


# 名前をもらって，どの分類かに書き換える関数．
function RawToNum(str)
    if str == "Iris-setosa"
        return [ 1.0, 0, 0 ]
    elseif str == "Iris-versicolor"
        return [ 0, 1.0, 0 ]
    else
        return [ 0, 0, 1.0 ]
    end
end

# この labels にベクトルの形で分類データが入る．
labels = RawToNum.(labels_raw)

150-element Array{Array{Float64,1},1}:
 [1.0, 0.0, 0.0]
 [1.0, 0.0, 0.0]
 [1.0, 0.0, 0.0]
 ⋮
 [0.0, 0.0, 1.0]
 [0.0, 0.0, 1.0]
 [0.0, 0.0, 1.0]

なぜこんな形で分類結果を表記するのかは，NN の出力と合わせるためだ．あとでわかってくるだろうからこの時点ではあまり気にしなくて良い．

さて次に，このデータのうち一部を「学習後の NN の能力チェック用」に分離してとっておき，それには NN の学習が済むまで参照しないようにしよう．全部でたった 150個しかデータがないのでもったいないが，これを別にしておかないと能力チェックが困難になってしまう．

1
2
3
4
5
6


# 学習後のチェックに使うデータをとっておく．学習には用いない．
# 3種類の花のデータを5個ずつ，チェック用に抜き出しておく．

toCheckIDs = vcat( 46:50, 96:100, 146:150 )  
features_raw_toCheck = features_raw[:, toCheckIDs ]
labels_toCheck = labels[toCheckIDs]

15-element Array{Array{Float64,1},1}:
 [1.0, 0.0, 0.0]
 [1.0, 0.0, 0.0]
 ⋮

残りは学習に使えるデータだ．

1
2
3
4
5


# 学習に使うデータ．

SampleIDs = setdiff( 1:150, toCheckIDs )
features_raw_sample = features_raw[:, SampleIDs ]
labels_sample = labels[SampleIDs]

135-element Array{Array{Float64,1},1}:
 [1.0, 0.0, 0.0]
 [1.0, 0.0, 0.0]
 ⋮

次に，花のがく片の長さ…等の数字を正規化しよう．それぞれの数字の大きさ等が異なるのに NN で混ぜるのは NN の性能を下げるだけなので，こうしておこう．

1
2
3
4
5
6
7
8


# 入力データの数字的な偏りをなるべくなくしておく．
# ただし，事前に使える平均，偏差はサンプル値からしかとれない.

Std = [ std( features_raw_sample[i, :] ) for i in 1:4 ]
Mean = [ mean( features_raw_sample[i, :] ) for i in 1:4 ]

features_toCheck = (features_raw_toCheck .- Mean) ./ Std
features_sample  = (features_raw_sample  .- Mean) ./ Std

さて，肝心の NN そのものを定義しよう．先の例題よりずっと難しいはずの問題だから，少し n を大きくし，また中間層も増やそう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38


# NN の定義．少し層を増やした．まあこれでも小さい方だな．

n = 20

function nn(M, input) 
    Ci = view( M, :, 1:4 )
    bi = view( M, :, 5 )

    C1 = view( M, :, 6:n+5 )
    b1 = view( M, :, n+6 )

    C2 = view( M, :, n+7:2n+6 )
    b2 = view( M, :, 2n+7 )

    C3 = view( M, :, 2n+8:3n+7 )
    b3 = view( M, :, 3n+8 )

    C4 = view( M, :, 3n+9:4n+8 )
    b4 = view( M, :, 4n+9 )

    C5 = view( M, :, 4n+10:5n+9 )
    b5 = view( M, :, 5n+10 )

    Co = ( view( M, :, 5n+11:5n+13 ) )' # 転置
    bo = view( M, 1:3, 5n+14 )

    r1 =  sigmoid.( Ci * input + bi ) # 入力値処理

    r2 = sigmoid.( C1 * r1 + b1 ) 
    r3 = sigmoid.( C2 * r2 + b2 ) # 中間層．ReLU や TanhShrink だとうまくいかない．
    r4 = sigmoid.( C3 * r3 + b3 )
    r5 = sigmoid.( C4 * r4 + b4 )
    r6 = sigmoid.( C5 * r5 + b5 )

    output = softmax( Co * r6 + bo ) # 出力値処理

    return output
end

あとは誤差(損失関数)を定義し，パラメータの初期値を用意すれば良い．今回はこうした分類問題での損失関数として使われる定番のクロスエントロピーを使ってみよう⁴．

1
2
3
4
5


# 結果の誤差は，分類問題での定番である crossentropy にて．
loss( output, v_true ) = Flux.crossentropy( output, v_true )

# NN のパラメータ行列 H の初期値を乱数で生成．これを少しずつ修正する．
H = 10.0 * ( rand(n,5n+14) .- 0.5 )

20×114 Array{Float64,2}:
 -2.69872    4.57275   -1.22044    …  -1.91681     3.91092   -3.5388
 -2.9915    -1.99061    1.77325        2.48023     3.70738    4.05232
 -3.27424    2.83662   -1.68226       -0.481219    0.226912   3.85234
  4.80131    1.52694   -0.40866        3.49361    -1.90544    0.247762
 -2.86762   -4.7581     3.69804        0.0691466   1.67901   -4.7041
 …
 -3.76627    4.71857   -0.785994   …  -3.53204     0.51036   -1.61283
  4.65462    0.155111  -1.06677       -4.4002      4.79697   -3.02118
 -0.904377   1.00613    0.0831876      2.2009      3.73551   -0.146672
 -2.16668    4.22355   -4.95464        0.900292   -1.46091    0.253256
  3.45072    0.147795   4.43228        2.97151    -2.85828   -1.84148

少し強引だが，下記のように学習させてしまおう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


# NN の学習

# 誤差の式を簡単に書いておいて…
g(H, i) = loss( nn(H, features_sample[:, i]), labels_sample[i] ) 

itr = 500
datasize = size(labels_sample)[1]

@showprogress for i in 1:(itr * datasize)
    
   num = rand(1:datasize) # データの順序に依存しないように乱数で

   grad_f = Flux.gradient(M -> g(M, num), H)[1] 
   # 誤差の H に対する勾配. 
   # 今回は Flux の gradient を使う.
   # Flux の gradient は ForwardDiff の gradient と
   # 本質的に中身は同じだが，出力方法が少し違う.

   grad_size = norm(grad_f)^2 # 勾配の大きさ

   if grad_size < 0.01 # 学習係数の調整(数字は適当)
        γ = 0.1
    else
        γ = g(H,num) / grad_size
    end

    H +=  -γ * grad_f # パラメータ H を修正．
end

Progress: 100%|███████████████████████████████| Time: 0:00:20

うまく学習できたか，少し見てみよう．まずはサンプルデータの1番目だ．

1
2
3
4


# チェックのための簡易表記
nn_sample(i) = nn( H, features_sample[:, i] )

nn_sample(1)

3-element Array{Float64,1}:
 0.9999895151391504
 9.655343976072604e-6
 8.295168736658137e-7

この出力は，まあ，NN がどの分類であるかの確率出力を出した，と思えば良い．だからこの場合は 1種類目のアヤメの確率が高いと言っているわけだ．

そして実際にはどうかというと，

1

labels_sample[1]

3-element Array{Float64,1}:
 1.0
 0.0
 0.0

となっているので，これは「正解」だということになる．

あと 2点ほど手動でチェックしてみよう．次に，2種類目のアヤメのデータであるはずの 70番目のデータに対する NN の出力を見ると，

1

nn_sample(70)

3-element Array{Float64,1}:
 1.0450317543938049e-5
 0.9999844089491658
 5.140733290340332e-6

となっており，やはりこの場合も正しく学習できていることがわかる．

同様に，3種類目のアヤメのデータである 130番目のデータを NN に入力すると，

1

nn_sample(130)

3-element Array{Float64,1}:
 7.726796383260256e-8
 1.1397093547778112e-6
 0.9999987830226813

となり，このデータに対してもやはり正しく学習できていることが確認できる．

実際，この場合はすべて正しく学習できていて(初期値が乱数によるので，もちろん人によって異なりうるが), 次のように確かめられる．まず，NN の確率出力をもらってどう判断するか，という操作を次のような関数にしよう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


# 出力値による判断を明確にする関数
function decision(x)
  v = similar(x)
  max_i = argmax(x)

  for i in 1:size(x)[1]
    if i == max_i
      v[i] = 1.0
    else
      v[i] = 0.0
    end
  end

  return v
end

こうしておいて，学習に使ったサンプルデータと，NN の出力による判断値の違いを次のようにまとめる．

1

error_sample = labels_sample - decision.( nn_sample.(1:135) )

135-element Array{Array{Float64,1},1}:
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 ⋮
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]

少なくとも学習はうまくいっているように見える．一つもミスがないか確かめておこう．

1

sum( norm.(error_sample) )

0.0

うむ，学習に使ったデータに対しては 100% の学習ができたことがこれで確認できた．

では，肝心の，「初めてみるデータに対して確かに NN は判断ができるか」をチェックしよう．まずは手動でいくつか確認してみよう．

1
2
3
4


# 初めて見るデータに対しての NN の判断
nn_toCheck(i) = nn( H, features_toCheck[:, i])

nn_toCheck(1)

3-element Array{Float64,1}:
 0.9999894672043542
 9.482008512301156e-6
 1.0507871334468467e-6

ふむ，これは本来の 46番目のデータ(花は一種類目)に対する NN の判断だが，確かに正しい．

ほかも見てみよう．

1

nn_toCheck(6)

3-element Array{Float64,1}:
 1.4295460493849339e-5
 0.9999795612987193
 6.143240786718024e-6

そしてこれは本来の 96番目のデータ(花は二種類目)に対する NN の判断だ. これも確かに正しい．

次はどうかな．

1

nn_toCheck(11)

3-element Array{Float64,1}:
 5.5972916215434685e-8
 9.357544525378509e-7
 0.9999990082726312

これは本来の 146番目のデータ(花は三種類目)に対する NN の判断で，これも確かに正しいな．

NN が知らない15個のデータに対して一気にチェックしよう．

1

error_toCheck = labels_toCheck - decision.( nn_toCheck.(1:15) )

15-element Array{Array{Float64,1},1}:
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]
 [0.0, 0.0, 0.0]

おお！エラー無し！ちょっと出来すぎの気もするが，学習後のこの NNは，知らないデータ 15個に対しても 100% の正しい判断を下したぞ！すごいもんだな．

というわけで，今回は文句なし，十分な機械学習ができたと言えよう．ただし，過学習(過学習についてはレポートにて)の恐れはあるのでそこは調べておいて，機械学習の現場では忘れないようにしよう．

レポート

以下の課題について能う限り賢明な調査と考察を行い，
2021-AppliedMath7-Report-15
という題名をつけて e-mail にて教官宛にレポートとして提出せよ. なお，レポートを e-mail の代わりに TeX で作成した書面にて提出してもよい.

課題

最初の例題の 2次元バージョンとでもいうべき次の問題に取り組んでみよう．

具体的には，図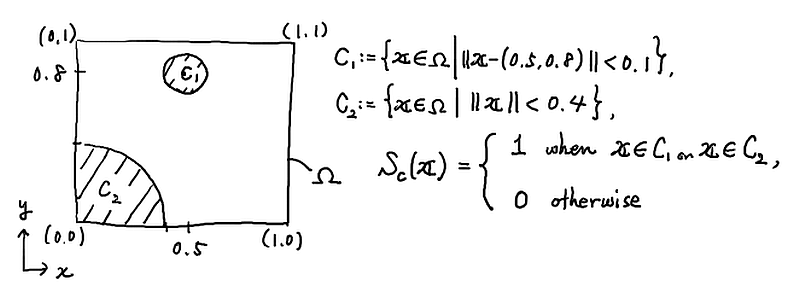
の中で定義される関数 $S_c$ に従ってデータ $D = \{ \boldsymbol{x}_k, \boldsymbol{y}_k = S_c(\boldsymbol{x}_k) \}_{k=1}^N$ が $N \cong 10,000$ 程度で得られているとする($N$ は好きに設定して良い)．

関数 $S_c$ が未知である想定のもとに，今回の授業と同様に NN を構成し，データ $D$ を使ってパラメータを学習させて，NN が関数 $S_c$ を近似的に構成するようにしてみよう．

注: この問題は，2つのパラメータ( $\Omega$ 上の座標 $(x,y)$ のこと)から 2種類の分類(0 か 1 か)ができるように，という機械学習を行うことに相当する．
授業資料ではアヤメの分類に「がくの長さ，幅，花びらの長さ，幅」という 4つの数字を使う NN を作り，学習させた．しかし，授業資料でも見たように「がくの長さ，幅，花びらの長さ」という 3つの数字でも十分にアヤメの分類が可能なように思われる．

そこで，「がくの長さ，幅，花びらの長さ」という 3つの数字を使う NN を作り，学習させてみよう．そして学習後の NN がどれくらい分類を正確にできるか，その正解率などをチェックしてみよ．
「過学習」について，文献などを用いて調べ，自分なりに対応策を考えてみよう．考えた対応策がうまくいくかは，細かい工夫によって随分変わったりするので，ここではそこまで実現可能性や効率等についてあまり考えなくて良い．

どちらかというと，この $\gamma > 0$ は最小化問題での用語に関連した言い方(ステップ幅と言っている人もいるようだ)をしたほうが筋が良いよね．もちろん学習係数と呼んでもいいんだけどね． ↩︎
もちろん，実際の問題はデータ集めからして大変なわけで，そうそうお気楽に考えてはいかんが． ↩︎
MLDatasets パッケージの機能は以前は Flux パッケージに含まれていたものだ．今でも一応含まれているが，いずれ削除されるだろうから今から分けておくのがベターだね． ↩︎
2つの分布間の距離「っぽいもの」として使う今回のようなケースでは，対称性が無いクロスエントロピー(交差エントロピーとも言う)は数学的には問題がある，という考え方もある．まあ，よく使われるので実用性はそれなりにあると思っていいだろう． ↩︎