偏微分方程式: 多次元問題
空間次元が多次元の偏微分方程式
空間次元が 2以上の偏微分方程式を扱ってみよう. 今回は試しに、常微分方程式に空間変数を 2つ導入して偏微分方程式へ拡張し、計算してみよう.
Volterra 問題を例として
以前扱った Volterra 問題は、自由変数が時間だけの常微分方程式で、これは、生物の数がどこでも一定ということを前提としていることを意味していた. しかし、実際の生物は空間分布が一定ではないし、そしておそらく、この空間分布に偏りがあることが生物の数量変化に大きな影響を与える結構重要なファクターなんじゃないかな.
そこで、空間変数を自由変数として導入し、問題を偏微分方程式にして取り扱ってみよう. しかも、こういう問題は空間次元が 1のときと 2以上のときとで根本的に挙動が異なるので、思い切って空間次元を 2以上にとって、取り扱ってみよう.
最初は, おとなしめなモデルで
空間変数を新たに導入するということは、問題のモデルに新しいファクターを導入する必要が生ずる. もちろんいろいろなファクターがあり得るので、本来は慎重に考えないといけないところだ.
しかし今回は数値計算への熟達が主眼であるので、モデルとしては少し安直に、「常微分方程式からのズレがあまり無い」モデルを導入し、数値計算結果の解釈に苦労しなくて良いようにしよう.
そこで、単なる「拡散」だけを導入することにして、被食者数を $u(x, t)$ で、捕食者数を $v(x, t)$ で表すとして、 $x \in [0, L] \times [0, L]$, $t > 0$ とし、以下のようなモデルを考えよう.
$\left\{\begin{array}{rcl} \displaystyle \frac{\partial u}{\partial t} & = & \epsilon_1 \Delta u - C_1 uv + D_1 u, \cr\cr \displaystyle \frac{\partial v}{\partial t} & = & \epsilon_2 \Delta v + C_2 uv - D_2 v \end{array}\right.$
ただし、係数 $\epsilon_1$, $\epsilon_2$, $C_1$, $C_2$, $D_1$, $D_2$ は全て定数で正としておこう.
そして、空間領域に関する境界条件としては周期的境界条件を課しておくことにしよう.
method of line を適用する
ここでは、空間領域 $\Omega = [0, L] \times [0, L]$ に対し、その分割数を $N \times N$ とし、境界条件として周期的境界条件を離散化しよう.
よって、$\Delta x = \Delta y = L / N$ として $u(x,t)$ の離散化に相当する従属変数を $ u(t) = \{ u_{i,j}(t)\}_{i, j = 1}^N$ とし、境界条件は 外側にはみ出す点を仮想的に考えたとして
\[ \left\{ \begin{array}{rcl} \displaystyle u_{0, j} & := & u_{N, j} {\rm \,\,\, for \,\,\,} \forall j ,\cr\cr \displaystyle u_{N+1, j} & := & u_{1, j} {\,\,\, 同上 } , \cr\cr \displaystyle u_{i, 0} & := & u_{i, N} {\rm \,\,\, for \,\,\,} \forall i, \cr\cr \displaystyle u_{i, N+1} & := & u_{i, 1} {\,\,\, 同上 } \end{array} \right. \]
と解釈することになる.
こうしておいて、空間微分(ラプラシアン) $\Delta$ をたとえば差分近似で置き換える. たとえば $U$ に対する二階中心差分ならば
\[ (\Delta u)_{i,j} := \frac{ u_{i+1,j} + u_{i-1,j} + u_{i,j+1} + u_{i,j+1} - 4 u_{i,j} }{\Delta x^2} \]
となる(ただし,$\Delta x = \Delta y$ としている前提のもとでのこと,ということに注意). これらを使った場合は、全体は $i = 1,2,\cdots, N$, $j = 1,2,\cdots, N$ に対して
\[ \left\{ \begin{array}{rcl} \displaystyle \frac{d u_{i,j}(t) }{dt} & = & \epsilon_1 (\Delta u)_{i,j} - C_1 u_{i,j} v_{i,j} + D_1 u_{i,j}, \cr\cr \displaystyle \frac{d v_{i,j}(t) }{dt} & = & \epsilon_2 (\Delta v)_{i,j} + C_2 u_{i,j} v_{i,j} - D_2 v_{i,j}, \cr \end{array} \right. \]
という $N \times N$ 元連立常微分方程式で近似できることになる.
あとは少しずつプログラムを作っていくだけだ. まずは、問題のパラメータを設定してしまおう.
|
|
次に、ラプラシアンをどうにか構成しよう. まず、そのために使う係数行列を下記のように定義する.
|
|
40×40 SparseMatrixCSC{Float64,Int64} with 120 stored entries: [1 , 1] = -3200.0 [2 , 1] = 1600.0 [40, 1] = 1600.0 [1 , 2] = 1600.0 [2 , 2] = -3200.0 [3 , 2] = 1600.0 [2 , 3] = 1600.0 [3 , 3] = -3200.0 [4 , 3] = 1600.0 [3 , 4] = 1600.0 [4 , 4] = -3200.0 [5 , 4] = 1600.0 ⋮ [36, 37] = 1600.0 [37, 37] = -3200.0 [38, 37] = 1600.0 [37, 38] = 1600.0 [38, 38] = -3200.0 [39, 38] = 1600.0 [38, 39] = 1600.0 [39, 39] = -3200.0 [40, 39] = 1600.0 [1 , 40] = 1600.0 [39, 40] = 1600.0 [40, 40] = -3200.0
こうしておいて、近似データそのものである行列 $u$ に対して、上で定義した行列 $d2$ を用いた $d2 * u$ は行列 $u$ の行添字に関する二階差分になっている.
同様に、$u * d2$ は行列 $u$ の列添字に関する二階差分になっているので、 結局、これらの和である $d2 * u + u * d2$ は $u$ に(離散)ラプラシアンを適用した結果になる.
tips: 線形代数が苦手な人は、for 文を使ってプログラムしたほうが良いかも.
よって、微分方程式の右辺の近似計算式は次のようになるだろう.
|
|
f (generic function with 1 method)
ちなみに、上をよく見ると分かるように、 $u(x)$ の近似行列 $u_{i,j}$ と $v(x)$ の近似行列 $v_{i,j}$ を受け渡しする時は、上下につなげて、一つにして扱っている.
さて、これで連立常微分方程式の右辺(の近似)が計算できたことになるので、いつものように Runge-Kutta 法を定義する.
|
|
RK (generic function with 1 method)
これで計算手順の準備は整った.
次に、初期値を適当に作ろう. 今回は、ガウス型に穏やかに分布しているものを考えよう.
|
|
80×40 Array{Float64,2}: 0.300099 0.300152 0.300227 0.300332 … 0.300152 0.300099 0.300063 0.300152 0.300232 0.300347 0.300507 0.300232 0.300152 0.300097 0.300227 0.300347 0.300519 0.300759 0.300347 0.300227 0.300145 0.300332 0.300507 0.300759 0.301109 0.300507 0.300332 0.300212 0.300474 0.300725 0.301084 0.301584 0.300725 0.300474 0.300302 0.300661 0.301012 0.301513 0.302211 … 0.301012 0.300661 0.300422 0.300902 0.30138 0.302064 0.303016 0.30138 0.300902 0.300576 0.301202 0.301839 0.302751 0.304021 0.301839 0.301202 0.300768 0.301566 0.302396 0.303584 0.305238 0.302396 0.301566 0.301
0.301994 0.303051 0.304563 0.306669 0.303051 0.301994 0.301273 0.302481 0.303796 0.305677 0.308298 … 0.303796 0.302481 0.301584 0.303016 0.304616 0.306903 0.310089 0.304616 0.303016 0.301926 0.303584 0.305485 0.308203 0.311989 0.305485 0.303584 0.302289 ⋮ ⋱
0.4 0.4 0.4 0.4 0.4 0.4 0.4
0.4 0.4 0.4 0.4 0.4 0.4 0.4
0.4 0.4 0.4 0.4 … 0.4 0.4 0.4
0.4 0.4 0.4 0.4 0.4 0.4 0.4
0.4 0.4 0.4 0.4 0.4 0.4 0.4
0.4 0.4 0.4 0.4 0.4 0.4 0.4
0.4 0.4 0.4 0.4 0.4 0.4 0.4
0.4 0.4 0.4 0.4 … 0.4 0.4 0.4
0.4 0.4 0.4 0.4 0.4 0.4 0.4
0.4 0.4 0.4 0.4 0.4 0.4 0.4
0.4 0.4 0.4 0.4 0.4 0.4 0.4
0.4 0.4 0.4 0.4 0.4 0.4 0.4
どんな初期値なのか、目で見ておこう.
まずは u の初期値で、
|
|
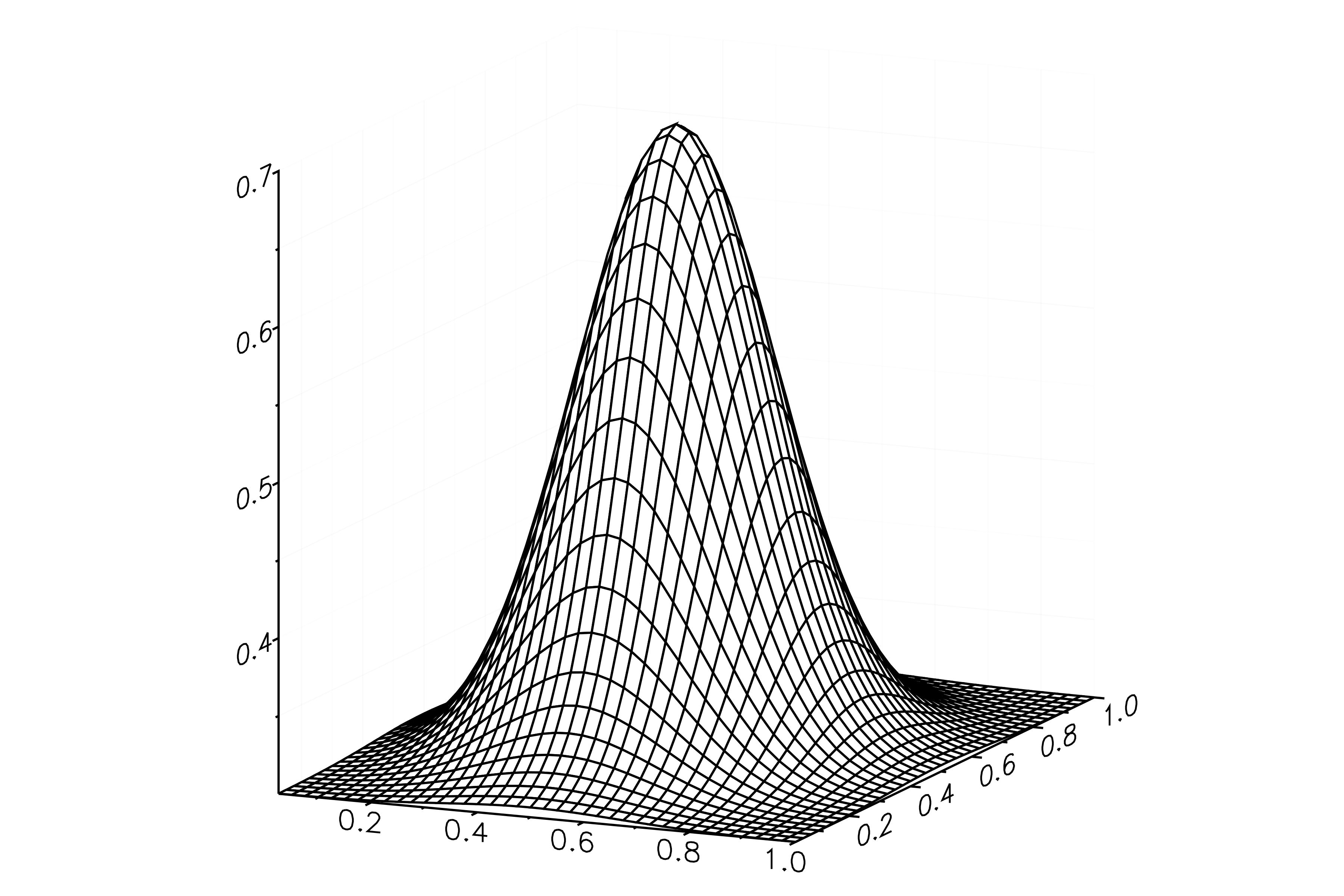
次は v の初期値だ.
|
|
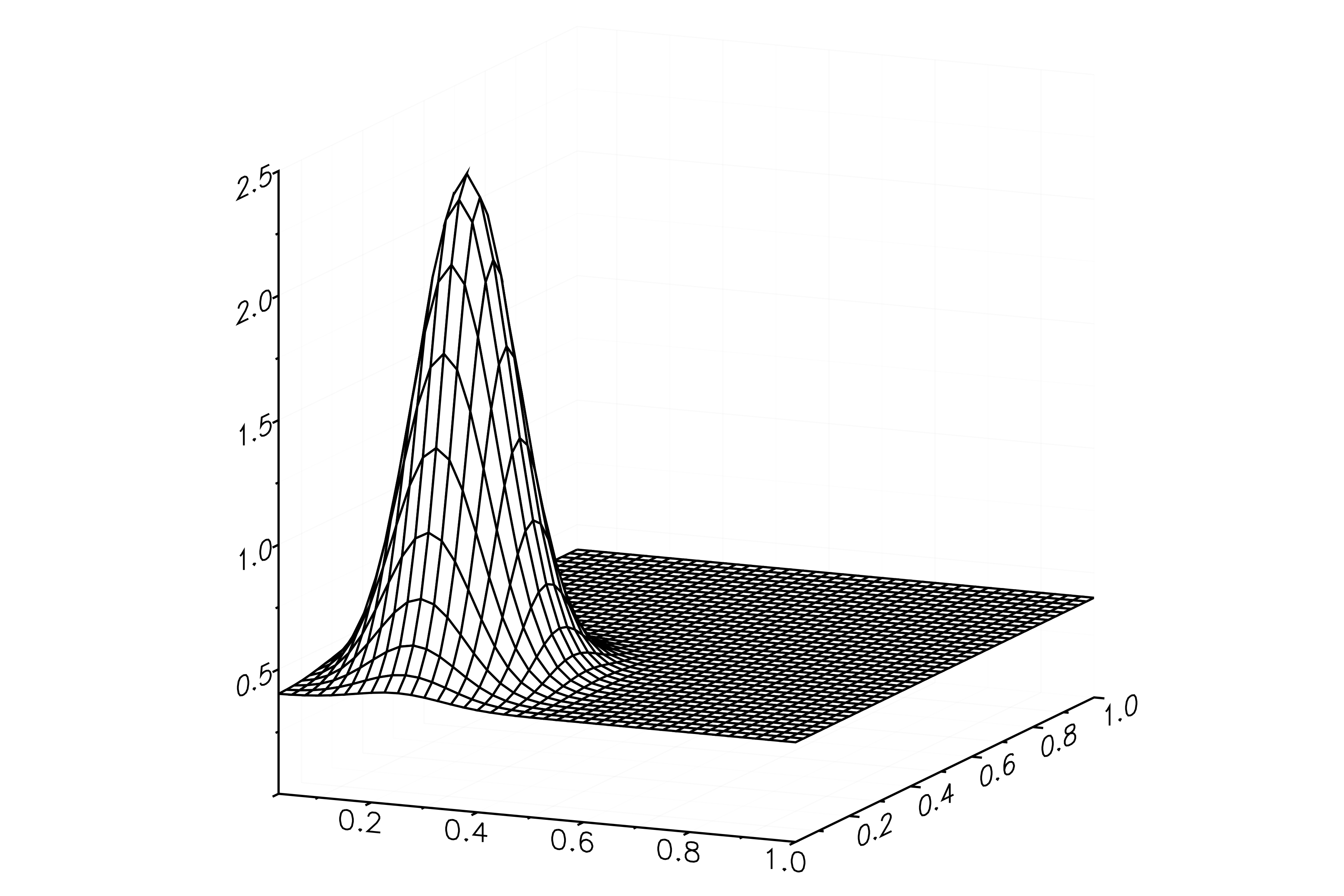
ふむ、こんな感じか.中心位置がずらしてあることに留意しておこう.
さて、これで準備は整ったので、早速、計算してみよう. Juliabox が混んでいなければ、2分未満で計算が終わるだろう.
|
|
Progress: 100%|█████████████████████████████████████████| Time: 0:01:41
試しに結果の数字をちょろっと見てみる.
|
|
80×40×101 Array{Float64,3}: [:, :, 1] = 0.300099 0.300152 0.300227 0.300332 … 0.300152 0.300099 0.300063 0.300152 0.300232 0.300347 0.300507 0.300232 0.300152 0.300097 0.300227 0.300347 0.300519 0.300759 0.300347 0.300227 0.300145 0.300332 0.300507 0.300759 0.301109 0.300507 0.300332 0.300212 0.300474 0.300725 0.301084 0.301584 0.300725 0.300474 0.300302 0.300661 0.301012 0.301513 0.302211 … 0.301012 0.300661 0.300422 0.300902 0.30138 0.302064 0.303016 0.30138 0.300902 0.300576 0.301202 0.301839 0.302751 0.304021 0.301839 0.301202 0.300768 0.301566 0.302396 0.303584 0.305238 0.302396 0.301566 0.301
0.301994 0.303051 0.304563 0.306669 0.303051 0.301994 0.301273 0.302481 0.303796 0.305677 0.308298 … 0.303796 0.302481 0.301584 0.303016 0.304616 0.306903 0.310089 0.304616 0.303016 0.301926 0.303584 0.305485 0.308203 0.311989 0.305485 0.303584 0.302289 ⋮ ⋱
1.47918 1.46855 1.45163 1.42908 1.4705 1.48019 1.48312 1.49623 1.48632 1.47059 1.44961 1.48848 1.49734 1.49995 1.51275 1.50355 1.48902 1.46966 … 1.50609 1.51405 1.51629 1.52827 1.51975 1.50641 1.48866 1.52287 1.52986 1.53168 1.54238 1.53448 1.52225 1.50608 1.53836 1.54437 1.54572 1.55472 1.54736 1.53617 1.52148 1.55218 1.55718 1.55803 1.56499 1.5581 1.54786 1.53454 1.56396 1.56799 1.56833 1.57303 1.56655 1.55715 1.54508 … 1.57343 1.57655 1.57641 1.57875 1.57264 1.564 1.55306 1.5804 1.58273 1.58216 1.58217 1.57643 1.56852 1.55862 1.58475 1.58645 1.58556 1.58341 1.5781 1.5709 1.56199 1.58645 1.58774 1.58668 1.58265 1.57785 1.57141 1.56347 1.58556 1.58668 1.58565
あまり変なことにはなっていなさそうなので、プロットしてみよう.
まず最大値と最小値を調べておいて…
|
|
(0.1976488027884744, 2.865361858704632)
最初に contour プロットで、試しに、fill=true をつけて、色を塗って平面で表してもらおう.
|
|
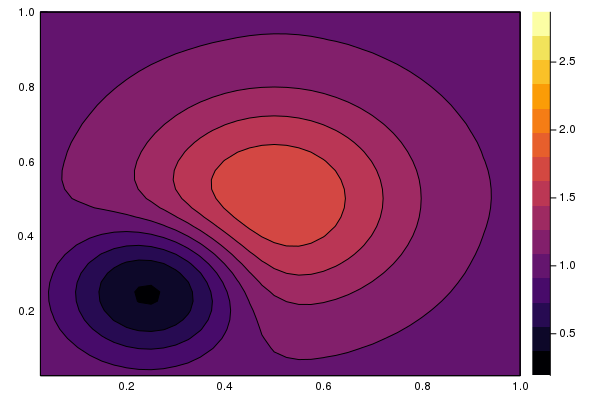
普通に、wireframe で見てみると次のような感じだな.
|
|
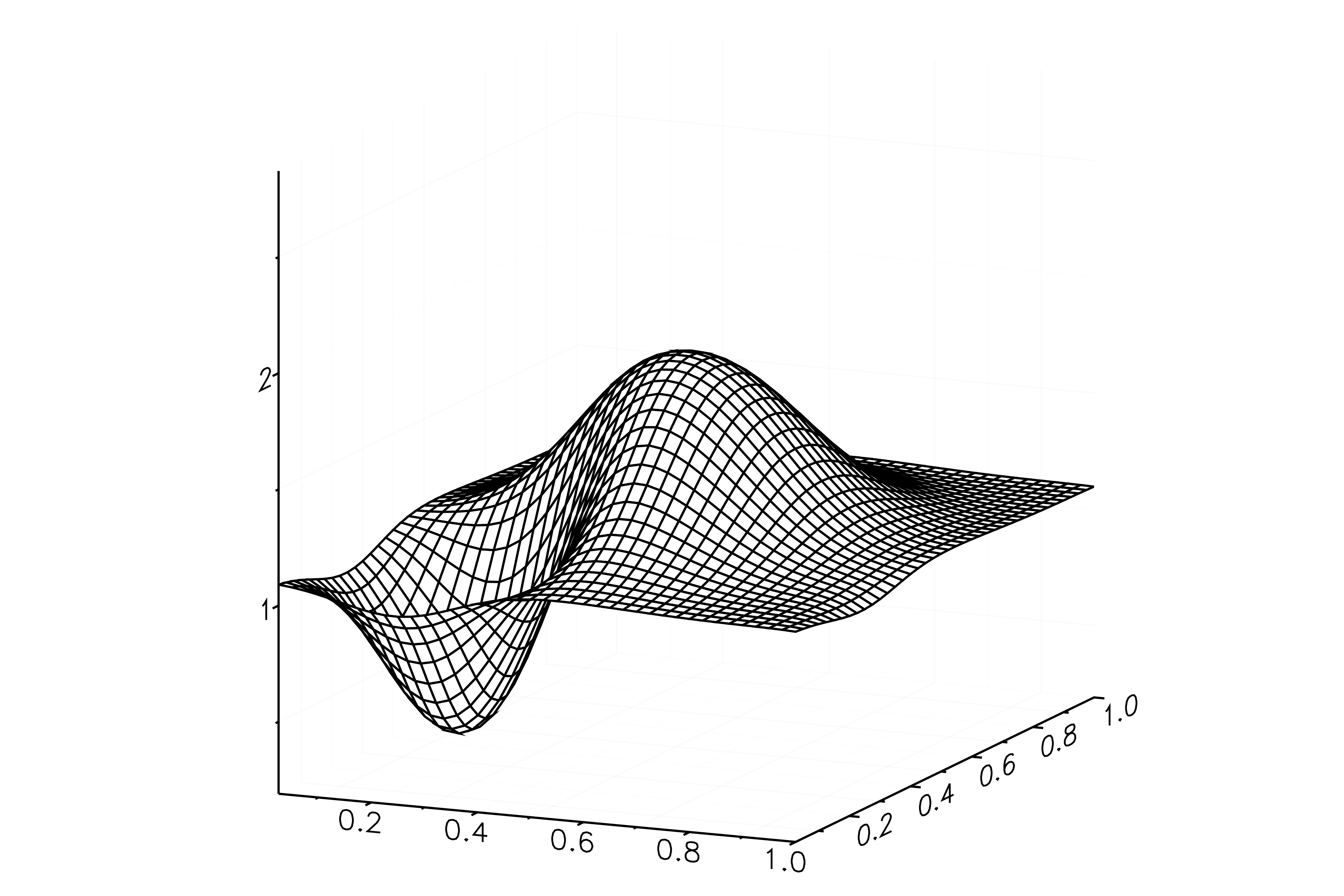
ふむ、なんとなくうまく計算できているようだ. しかし、いちいち plot コマンドを打って確認するのも疲れるので、一気に全データを画像にしてしまうことを考えよう.
まず、$U$ と $V$ のたくさんの画像ファイルを入れておくディレクトリをコマンドで作らせよう.これは一回だけやれば良い.
|
|
注: 上の2つの “mkdir” の実行後、juliabox のファイルビューアー部分を見てみよう.U, V という新しいディレクトリができているはずだ.
次に、データを画像ファイルとして保存するコマンドを作ろう. 基本的には、plot 系コマンドの直後に savefig コマンドを使うだけで、そのグラフを画像ファイルとして保存できる. 今回は動画ファイルの「元」にしたいので、そうだなあ、”4桁の数字.png” というファイル名になるようにしておく.
|
|
注: “@sprintf” というマクロは、昔から C 系統のプログラム言語で使われている sprintf 命令を模したもので、文字列を「決まったフォーマットで出力する」ものだ.使い方は “sprntf” などで検索してみよう.
では、全データからたくさんの画像ファイルを作ろう.PC だと10秒ぐらい、juliabox だと空いていれば 30秒ぐらいでおわるかな.
|
|
Progress: 100%|█████████████████████████████████████████| Time: 0:00:25
ffmpeg などの動画作成ツールで動画にしてみよう
フリーのツールで ffmpeg というものがあり、これを使うと連番の画像ファイルを無理なくきれいに動画にできる. この手法は便利なので覚えておこう.
今の juliabox にはこれがインストールされていて使えるので見逃す手は無い. 自分の PC で実習をしていて ffmpeg がインストールされていない、という人は、これを機にインストールしておこう.
さて、今回は ffmpeg を julia から直接呼び出して使ってみよう. 以下のようにすればよいだろう.
(詳しい人向け: terminal からコマンドを打っても良い)
|
|
ffmpeg version 2.8.15-0ubuntu0.16.04.1 Copyright © 2000-2018 the FFmpeg developers built with gcc 5.4.0 (Ubuntu 5.4.0-6ubuntu1~16.04.10) 20160609 configuration: –prefix=/usr –extra-version=0ubuntu0.16.04.1 –build-suffix=-ffmpeg –toolchain=hardened –libdir=/usr/lib/x86_64-linux-gnu –incdir=/usr/include/x86_64-linux-gnu –cc=cc –cxx=g++ –enable-gpl –enable-shared –disable-stripping –disable-decoder=libopenjpeg –disable-decoder=libschroedinger –enable-avresample –enable-avisynth –enable-gnutls –enable-ladspa –enable-libass –enable-libbluray –enable-libbs2b –enable-libcaca –enable-libcdio –enable-libflite –enable-libfontconfig –enable-libfreetype –enable-libfribidi –enable-libgme –enable-libgsm –enable-libmodplug –enable-libmp3lame –enable-libopenjpeg –enable-libopus –enable-libpulse –enable-librtmp –enable-libschroedinger –enable-libshine –enable-libsnappy –enable-libsoxr –enable-libspeex –enable-libssh –enable-libtheora –enable-libtwolame –enable-libvorbis –enable-libvpx –enable-libwavpack –enable-libwebp –enable-libx265 –enable-libxvid –enable-libzvbi –enable-openal –enable-opengl –enable-x11grab –enable-libdc1394 –enable-libiec61883 –enable-libzmq –enable-frei0r –enable-libx264 –enable-libopencv libavutil 54. 31.100 / 54. 31.100 libavcodec 56. 60.100 / 56. 60.100 libavformat 56. 40.101 / 56. 40.101 libavdevice 56. 4.100 / 56. 4.100 libavfilter 5. 40.101 / 5. 40.101 libavresample 2. 1. 0 / 2. 1. 0 libswscale 3. 1.101 / 3. 1.101 libswresample 1. 2.101 / 1. 2.101 libpostproc 53. 3.100 / 53. 3.100 Input #0, image2, from ‘U/%04d.png’: Duration: 00:00:04.04, start: 0.000000, bitrate: N/A Stream #0:0: Video: png, rgb24(pc), 3600x2400, 25 fps, 25 tbr, 25 tbn, 25 tbc [libx264 @ 0x199fe40] using cpu capabilities: MMX2 SSE2Fast SSSE3 SSE4.2 AVX FMA3 AVX2 LZCNT BMI2 [libx264 @ 0x199fe40] profile High, level 3.2 [libx264 @ 0x199fe40] 264 - core 148 r2643 5c65704 - H.264/MPEG-4 AVC codec - Copyleft 2003-2015 - http://www.videolan.org/x264.html - options: cabac=1 ref=3 deblock=1:0:0 analyse=0x3:0x113 me=hex subme=7 psy=1 psy_rd=1.00:0.00 mixed_ref=1 me_range=16 chroma_me=1 trellis=1 8x8dct=1 cqm=0 deadzone=21,11 fast_pskip=1 chroma_qp_offset=-2 threads=24 lookahead_threads=4 sliced_threads=0 nr=0 decimate=1 interlaced=0 bluray_compat=0 constrained_intra=0 bframes=3 b_pyramid=2 b_adapt=1 b_bias=0 direct=1 weightb=1 open_gop=0 weightp=2 keyint=250 keyint_min=5 scenecut=40 intra_refresh=0 rc_lookahead=40 rc=crf mbtree=1 crf=23.0 qcomp=0.60 qpmin=0 qpmax=69 qpstep=4 ip_ratio=1.40 aq=1:1.00 Output #0, mp4, to ‘movie-u.mp4’: Metadata: encoder : Lavf56.40.101 Stream #0:0: Video: h264 (libx264) ([33][0][0][0] / 0x0021), yuv420p, 1200x800, q=-1–1, 5 fps, 10240 tbn, 5 tbc Metadata: encoder : Lavc56.60.100 libx264 Stream mapping: Stream #0:0 -> #0:0 (png (native) -> h264 (libx264)) Press [q] to stop, [?] for help frame= 101 fps=9.3 q=-1.0 Lsize= 2406kB time=00:00:19.80 bitrate= 995.3kbits/s
video:2404kB audio:0kB subtitle:0kB other streams:0kB global headers:0kB muxing overhead: 0.074096% [libx264 @ 0x199fe40] frame I:1 Avg QP: 9.81 size: 48272 [libx264 @ 0x199fe40] frame P:71 Avg QP:13.47 size: 27442 [libx264 @ 0x199fe40] frame B:29 Avg QP:19.79 size: 16012 [libx264 @ 0x199fe40] consecutive B-frames: 42.6% 57.4% 0.0% 0.0% [libx264 @ 0x199fe40] mb I I16..4: 46.6% 42.1% 11.4% [libx264 @ 0x199fe40] mb P I16..4: 1.0% 0.9% 2.3% P16..4: 1.8% 2.9% 5.1% 0.0% 0.0% skip:85.9% [libx264 @ 0x199fe40] mb B I16..4: 0.1% 0.5% 0.5% B16..8: 4.3% 3.4% 5.9% direct: 0.8% skip:84.4% L0:37.9% L1:30.9% BI:31.2% [libx264 @ 0x199fe40] 8x8 transform intra:28.5% inter:31.7% [libx264 @ 0x199fe40] coded y,uvDC,uvAC intra: 48.3% 0.0% 0.0% inter: 8.5% 0.0% 0.0% [libx264 @ 0x199fe40] i16 v,h,dc,p: 89% 6% 4% 0% [libx264 @ 0x199fe40] i8 v,h,dc,ddl,ddr,vr,hd,vl,hu: 10% 16% 56% 2% 2% 0% 4% 1% 7% [libx264 @ 0x199fe40] i4 v,h,dc,ddl,ddr,vr,hd,vl,hu: 10% 17% 20% 8% 9% 6% 11% 8% 10% [libx264 @ 0x199fe40] i8c dc,h,v,p: 100% 0% 0% 0% [libx264 @ 0x199fe40] Weighted P-Frames: Y:0.0% UV:0.0% [libx264 @ 0x199fe40] ref P L0: 60.8% 24.2% 9.6% 5.4% [libx264 @ 0x199fe40] ref B L0: 89.0% 11.0% [libx264 @ 0x199fe40] kb/s:974.64 ffmpeg version 2.8.15-0ubuntu0.16.04.1 Copyright © 2000-2018 the FFmpeg developers built with gcc 5.4.0 (Ubuntu 5.4.0-6ubuntu1~16.04.10) 20160609 configuration: –prefix=/usr –extra-version=0ubuntu0.16.04.1 –build-suffix=-ffmpeg –toolchain=hardened –libdir=/usr/lib/x86_64-linux-gnu –incdir=/usr/include/x86_64-linux-gnu –cc=cc –cxx=g++ –enable-gpl –enable-shared –disable-stripping –disable-decoder=libopenjpeg –disable-decoder=libschroedinger –enable-avresample –enable-avisynth –enable-gnutls –enable-ladspa –enable-libass –enable-libbluray –enable-libbs2b –enable-libcaca –enable-libcdio –enable-libflite –enable-libfontconfig –enable-libfreetype –enable-libfribidi –enable-libgme –enable-libgsm –enable-libmodplug –enable-libmp3lame –enable-libopenjpeg –enable-libopus –enable-libpulse –enable-librtmp –enable-libschroedinger –enable-libshine –enable-libsnappy –enable-libsoxr –enable-libspeex –enable-libssh –enable-libtheora –enable-libtwolame –enable-libvorbis –enable-libvpx –enable-libwavpack –enable-libwebp –enable-libx265 –enable-libxvid –enable-libzvbi –enable-openal –enable-opengl –enable-x11grab –enable-libdc1394 –enable-libiec61883 –enable-libzmq –enable-frei0r –enable-libx264 –enable-libopencv libavutil 54. 31.100 / 54. 31.100 libavcodec 56. 60.100 / 56. 60.100 libavformat 56. 40.101 / 56. 40.101 libavdevice 56. 4.100 / 56. 4.100 libavfilter 5. 40.101 / 5. 40.101 libavresample 2. 1. 0 / 2. 1. 0 libswscale 3. 1.101 / 3. 1.101 libswresample 1. 2.101 / 1. 2.101 libpostproc 53. 3.100 / 53. 3.100 Input #0, image2, from ‘V/%04d.png’: Duration: 00:00:04.04, start: 0.000000, bitrate: N/A Stream #0:0: Video: png, rgb24(pc), 3600x2400, 25 fps, 25 tbr, 25 tbn, 25 tbc [libx264 @ 0x1bafce0] using cpu capabilities: MMX2 SSE2Fast SSSE3 SSE4.2 AVX FMA3 AVX2 LZCNT BMI2 [libx264 @ 0x1bafce0] profile High, level 3.2 [libx264 @ 0x1bafce0] 264 - core 148 r2643 5c65704 - H.264/MPEG-4 AVC codec - Copyleft 2003-2015 - http://www.videolan.org/x264.html - options: cabac=1 ref=3 deblock=1:0:0 analyse=0x3:0x113 me=hex subme=7 psy=1 psy_rd=1.00:0.00 mixed_ref=1 me_range=16 chroma_me=1 trellis=1 8x8dct=1 cqm=0 deadzone=21,11 fast_pskip=1 chroma_qp_offset=-2 threads=24 lookahead_threads=4 sliced_threads=0 nr=0 decimate=1 interlaced=0 bluray_compat=0 constrained_intra=0 bframes=3 b_pyramid=2 b_adapt=1 b_bias=0 direct=1 weightb=1 open_gop=0 weightp=2 keyint=250 keyint_min=5 scenecut=40 intra_refresh=0 rc_lookahead=40 rc=crf mbtree=1 crf=23.0 qcomp=0.60 qpmin=0 qpmax=69 qpstep=4 ip_ratio=1.40 aq=1:1.00 Output #0, mp4, to ‘movie-v.mp4’: Metadata: encoder : Lavf56.40.101 Stream #0:0: Video: h264 (libx264) ([33][0][0][0] / 0x0021), yuv420p, 1200x800, q=-1–1, 5 fps, 10240 tbn, 5 tbc Metadata: encoder : Lavc56.60.100 libx264 Stream mapping: Stream #0:0 -> #0:0 (png (native) -> h264 (libx264)) Press [q] to stop, [?] for help frame= 101 fps=9.1 q=-1.0 Lsize= 2184kB time=00:00:19.80 bitrate= 903.7kbits/s
video:2182kB audio:0kB subtitle:0kB other streams:0kB global headers:0kB muxing overhead: 0.086277% [libx264 @ 0x1bafce0] frame I:1 Avg QP: 9.99 size: 57176 [libx264 @ 0x1bafce0] frame P:67 Avg QP:13.95 size: 26030 [libx264 @ 0x1bafce0] frame B:33 Avg QP:19.51 size: 13115 [libx264 @ 0x1bafce0] consecutive B-frames: 34.7% 65.3% 0.0% 0.0% [libx264 @ 0x1bafce0] mb I I16..4: 61.1% 24.2% 14.7% [libx264 @ 0x1bafce0] mb P I16..4: 1.1% 0.9% 2.2% P16..4: 2.0% 3.2% 5.1% 0.0% 0.0% skip:85.6% [libx264 @ 0x1bafce0] mb B I16..4: 0.1% 0.3% 0.4% B16..8: 4.3% 3.4% 4.8% direct: 0.9% skip:85.7% L0:31.9% L1:31.0% BI:37.0% [libx264 @ 0x1bafce0] 8x8 transform intra:23.3% inter:33.5% [libx264 @ 0x1bafce0] coded y,uvDC,uvAC intra: 48.0% 0.0% 0.0% inter: 8.5% 0.0% 0.0% [libx264 @ 0x1bafce0] i16 v,h,dc,p: 92% 5% 4% 0% [libx264 @ 0x1bafce0] i8 v,h,dc,ddl,ddr,vr,hd,vl,hu: 14% 11% 57% 2% 2% 1% 4% 2% 7% [libx264 @ 0x1bafce0] i4 v,h,dc,ddl,ddr,vr,hd,vl,hu: 11% 15% 19% 8% 10% 8% 10% 10% 9% [libx264 @ 0x1bafce0] i8c dc,h,v,p: 100% 0% 0% 0% [libx264 @ 0x1bafce0] Weighted P-Frames: Y:0.0% UV:0.0% [libx264 @ 0x1bafce0] ref P L0: 58.9% 24.3% 11.1% 5.7% [libx264 @ 0x1bafce0] ref B L0: 90.6% 9.4% [libx264 @ 0x1bafce0] kb/s:884.74
これで movie-u.mp4, movie-v.mp4 という2つの動画ファイルができたはずだ. julia/jyupiter のファイル操作画面で、その動画ファイルを view したり、ダウンロードして(jupyter はファイルを1つずつなら指定してから download できるぞ)動かしてみるなどして、確認しよう.
参考のために、そのファイルをここに直接おいておく.
- 得られる動画ファイル for u (mp4 形式)
- 得られる動画ファイル for v (mp4 形式)
Report No.12
- 上の実習例では
wireframeをベースに動画を作ったが、これをcontourをベースにしたものに替えて動画を作成してみよう. - 上の例では初期値をガウス分布っぽくしたものを扱ったが、これを乱数で生成してみよう.つまり、
|
|
として U0 を作ってから同様に計算して動画ファイルまで作ってみよう.
3. 今回は空間方向だけ差分化して、あとは常微分方程式として扱うという「線の方法」をとった.
時間方向も差分化したり、有限要素法を使ったり(かな-り面倒だが)他の方法で計算してみよう.
4. 今回は空間変数の導入にあたり「拡散効果」だけを導入したが、おそらく、「敵から逃げる」「餌を追う」という効果を導入したほうが生物モデルとしては妥当だろう.
それにはどうしたらよいか.いろいろ考えて、試してみよう.