多段解法, 予測子修正子法

常微分方程式の汎用解法: 線形多段解法や予測子修正子法を試してみよう

いろいろ慣れてきたところで、常微分方程式の汎用解法についてさらに学んでおこう．「以前学んだ Runge-Kutta 法で十分じゃないか」という気持ちもあるかもしれないが、ここで学ぶ他の解法にはまた違った性質が有るのでいずれ役に立つだろう．

今回は題材として、カオス現象を引き起こす有名な方程式の一つである Lorenz 方程式を扱ってみる．

式としては従属変数 $u=u(t)$, $v=v(t)$, $w=w(t)$ に対する以下の様な連立常微分方程式が Lorenz 方程式である．ただし、$\sigma$, $r$, $b$ は定数パラメータである．

\[ \left\{ \begin{array}{rcl} \displaystyle \frac{d u}{dt} & = & \sigma (-u + v), \cr\cr \displaystyle \frac{d v}{dt} & = & u (-w + r) - v, \cr\cr \displaystyle \frac{d w}{dt} & = & u v - b w . \end{array} \right. \]

パラメータはいろいろ取りうるが、典型的なものはザルツマンのパラメータと言って次のような値だ．ここではこれを採用しよう．

$\sigma = 10$, $r = 28$, $b = 8 / 3$ .

線形多段解法, 予測子修正子法について

線形多段解法(陽的アダムス法)

ここでは $du/dt = f(u,t)$ という常微分方程式を想定しよう(上の問題に対応させるなら、$(u,v,w)$ というベクトルをあらためて $u$ と書くと考えれば良い)． $t_n := n\Delta t$ と略記し、近似解や右辺の値なども $u_n \cong u(t_n)$, $f_n := f(u_n, t_n)$ と表記しよう．

そして、$t = t_n$ までは近似計算が進んでいて $u_{n+1}$ などを求める状況を考える．このとき、考えている常微分方程式の解に対して厳密に

\[ u(t_{n+1}) = u(t_n) + \int_{t_n}^{t_{n+1}} f(u(s), s) ds \]

が成り立つことから、近似解を

\[ u_{n+1} = u_n + \int_{t_n}^{t_{n+1}} f(u(s), s) ds \]

とする、と考えるのは悪くない発想だ．よって、この右辺の積分を近似すれば、全体が近似できたことになるのでそうしよう．

積分の近似には、たとえば $t \in [t_n, t_{n+1}]$ における $f(u(t),t)$ を $t$ の多項式などでうまく近似する、という方法がある．多項式の積分計算は簡単だしね．

そこで、どうにかして $f(u(t),t)$ を $t$ の多項式で近似することを考えよう．

計算過程の状況を考えると、すでに過去の近似計算過程によって、過去の値 $u_n, u_{n-1}, \cdots$ が求まっており、すなわち $f_n, f_{n-1}, \cdots$ も求まっている．

そこでこの $f_n, f_{n-1}, \cdots$ を使って $t \in [t_n, t_{n+1}]$ における $f(u(t),t)$ の $t$ による近似多項式を求めることを考えよう．

もう少し詳しく言うと、関数 $f$ の $l$ 個の離散値 $f_n, f_{n-1}, \cdots, f_{n-l+1}$ を用いて $t$ の $l-1$ 次多項式

\[ P_l(t) = C_0 + C_1 t + C_2 t^2 + \cdots + C_{l-1} t^{l-1} \]

で $f$ を近似しよう、というわけだ．

ちなみに、こういうケースのような任意の離散点での値を既知として得られる補間多項式を Legendre (補間)多項式 といい、その具体的な計算方法はいくつか知られている．ここではその計算方法のうち、この文脈で役に立つ Newton 補間多項式 (正確には Legendre 補間多項式の Newton 表示とでもいうべき)を使おう．具体的には上の $P$ は次のようになる．

\[ \begin{array}{rcl} P_l(t) & = & \displaystyle f_n + \left( \frac{f_n - f_{n-1}}{\Delta t}\right) (t - t_n) + \left( \frac{f_n - 2f_{n-1} + f_{n-2}}{\Delta t^2}\right) \frac{ (t - t_n)(t - t_{n-1}) }{2} + \cr\cr & & \displaystyle \cdots + \left( \frac{ \nabla^{l-1} f_n }{\Delta t^{l-1}} \right) \frac{ (t - t_n)(t - t_{n-1})\cdots(t - t_{n-l+1}) }{(l-1)!} . \end{array} \]

ただしここで $\nabla$ は後退差分作用素で、作用される数列の添字を一つ増やす作用素を $s$ として(だから、$s^{-1}$ は添字を一つ減らす作用素だね), $\nabla := ( 1 - s^{-1})$ と定義される．

この $P$ の積分範囲が $[t_n, t_{n+1}]$ であることから $t = t_n + a \Delta t$, $\, 0< a <1$ と変数変換することにしてこの式を整理すると、

\[ \hat{P_l}(a) = f_n + \nabla f_n \cdot a + \nabla^2 f_n \cdot a ( a+1 ) + \cdots + \nabla^{l-1} f_n \cdot a ( a+1 )( a+2 )\cdots(a+l-1) . \]

となる．さらに(一般)二項係数

\[ \left( n \atop k \right) = \frac{n (n-1) \cdots (n-k+1)}{k!} \]

を利用すると、より簡潔に

\[ \begin{array}{rcl} \hat{P_l}(a) & = & \displaystyle f_n - \nabla f_n \, \left( -a \atop 1 \right) + \nabla^2 f_n \, \left( -a \atop 2 \right) + \cdots + (-1)^{l-1} \nabla^{l-1} f_n \, \left( -a \atop l-1 \right) \cr\cr & = & \displaystyle \sum_{k=0}^{l-1} (-1)^{k-1} \nabla^{k-1} f_n \, \left( -a \atop k \right) . \end{array} \]

と書ける．

さて、これで近似多項式が得られたことになるので、これを積分しよう．つまり、

\[ \int_{t_n}^{t_{n+1}} P_l(t) dt = \Delta t \int_0^1 \hat{P_l}(a) da = \Delta t \sum_{k=0}^{l-1} \nabla^{k-1} f_n \, (-1)^{k-1} \int_0^1 \left( -a \atop k \right) da \]

となる.

そしてこの右辺の最後の部分にある $(-1)^{k-1} \int_0^1 \left( -a \atop k \right) da$ は具体的に計算できる．これを定数扱いして、$\gamma_k$ としよう．実際には、 $\gamma_0 = 1$, $\gamma_1 = 1 / 2$, $\gamma_2 = 5 / 12$, $\gamma_3 = 3 / 8$, $\gamma_4 = 251 / 720$, $\cdots$ といった数字になる．

これで最終的に、$l$ 個の離散値 $f_n, f_{n-1}, \cdots, f_{n-l+1}$ を用いた近似計算式

\[ u_{n+1} = u_n + \Delta t \sum_{k=0}^{l-1} \gamma_k \nabla^{k-1} f_n . \]

が得られたことになる．こうした近似計算法は、結果として離散値 $f_n, f_{n-1}, \cdots, f_{n-l+1}$ を線形に足し合わせるだけなので、一般に $l$ 段の線形多段解法 と呼ばれる．ここで導出したものは、既知の値(要するに過去の値)だけから計算できるので 陽的アダムス法 と呼ばれる．

陽的アダムス法の整理

上のようにして導出された陽的アダムス法を整理しておくと以下のようになる．

(1段. Euler 法と同じものになる) \[ u_{n+1} = u_n + \Delta t f_n . \]

(2段) \[ u_{n+1} = u_n + \Delta t \left( \frac{3}{2} f_n - \frac{1}{2} f_{n-1} \right) . \]

(3段) \[ u_{n+1} = u_n + \Delta t \left( \frac{23}{12} f_n - \frac{4}{3} f_{n-1} + \frac{5}{12} f_{n-2}\right) . \]

(4段) \[ u_{n+1} = u_n + \Delta t \left( \frac{35}{24} f_n - \frac{59}{24} f_{n-1} + \frac{37}{24} f_{n-2} - \frac{3}{8} f_{n-3} \right) . \]

注: web で検索するなどして、5段以上の陽的アダムス法を調べておこう．

陰的アダムス法

陽的アダムス法と異なり、新しい近似値による右辺の値 $f_{n+1}$ も多項式近似の参照値に使うのが陰的アダムス法である．他の考え方は同じなのでそこは省略して結果だけ書くと、(既知の離散値の個数を $l$ として)

\[ u_{n+1} = u_n + \Delta t \sum_{k=0}^l \tilde{\gamma_k} \nabla^{k-1} f_{n+1} \]

となる．ただし、

\[ \tilde{\gamma_k} := (-1)^k \int_0^1 \left( 1-a \atop k \right) da \]

で、これは $\tilde{\gamma_0} = 1$, $\tilde{\gamma_1} = -1 / 2$, $\tilde{\gamma_2} = -1 / 12$, $\tilde{\gamma_3} = -1 / 24$, $\tilde{\gamma_4} = -19 / 720$, $\cdots$ といった数字になる．

陰的アダムス法の整理

上のようにして導出された陰的アダムス法を整理しておくと以下のようになる．ただし、段数は「既知の離散値の個数 $l$」としてある．

(0段. 陰的 Euler 法と同じものになる) \[ u_{n+1} = u_n + \Delta t f_{n+1} . \]

(1段) \[ u_{n+1} = u_n + \Delta t \left( \frac{1}{2} f_{n+1} + \frac{1}{2} f_{n} \right) . \]

(2段) \[ u_{n+1} = u_n + \Delta t \left( \frac{5}{12} f_{n+1} + \frac{2}{3} f_{n} - \frac{1}{12} f_{n-1}\right) . \]

(3段) \[ u_{n+1} = u_n + \Delta t \left( \frac{3}{8} f_{n+1} + \frac{19}{24} f_{n} - \frac{5}{24} f_{n-1} + \frac{1}{24} f_{n-2}\right) . \]

注: web で検索するなどして、4段以上の陰的アダムス法を調べておこう．

予測子修正子法

予測子修正子法とは「精度は悪いが速い」近似解法と「精度は良いが遅い」近似計算法を組み合わせる一般的な方法である．一般的に書くとめんどくさいので、ここでは上の陽的アダムス法と陰的アダムス法を組み合わせた場合について例を述べることで紹介としよう．

まず、状況としては $u_n$, $f_n, f_{n-1}, \cdots, f_{n-l+1}$ が既知だとしよう．このとき、次のように各操作を定める．

操作	内容
操作 P (Predictor, 予測子)	陽的アダムス法によって $u_n$, $f_n, f_{n-1}, \cdots, f_{n-l+1}$ から近似値 $u_{n+1}$ を求める．
操作 E (Evaluator, 評価子)	持っている新しい近似値 $u_{n+1}$ を用いて $f_{n+1} = f(u_{n+1}, t_{n+1})$ を計算する.
操作 C (Corrector, 修正子)	陰的アダムス法の「右辺」を機械的に採用して $u_n$, $f_{n+1}, f_{n}, \cdots, f_{n-l+1}$ から近似値 $u_{n+1}$ を計算する.

すると、例えば操作として P, E, C, E の順番に操作をすると、陰的計算「無し」で新しい近似値 $u_{n+1}$ を得られることになる．さらにこれに加えて C, E の操作を繰り返すと、「収束して、本来の陰的アダムス法による近似値」$u_{n+1}$ に近い近似値が得られる可能性が高い．

注意操作 C は、本来の陰的アダムス法の「陰的性」を無視してあたかも陽的解法のようであるかのように用いている．つまり、本来の陰的アダムス法ではなく、その粗い近似をしていることになる．

プログラミングへ

最終的に、予測子を 3段の陽的アダムス法で、修正子をやはり 3段の陰的アダムス法としてプログラミングをしてみよう．

1
2


const σ, r, b = 10, 28, 8/3  # 定数の場合、const を宣言しておくと参照が速い！
Δt = 0.01

方程式の右辺を定義してしまおう．r はパラメータの名前ですでに使っているので、関数 f とでもしておこうか．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


function f(U)
    u, v, w = U
    
    return [
        σ * (-u + v)
        u * (- w + r) - v
        u*v - b*w
        ]
    
    end

線形多段解法では初期値が「余計にいくつか」必要だ．それらを求める方法はいろいろ考えられるが、まあ安直なのは Runge-Kutta 法かな．というわけで、Runge-Kutta 法による時間発展もプログラミングしてしまおう．

1
2
3
4
5
6
7


function RK(U)
    f1 = f(U)
    f2 = f(U + Δt/2 * f1)
    f3 = f(U + Δt/2 * f2)
    f4 = f(U + Δt * f3)
    return U + Δt * (f1 + 2*f2 + 2*f3 + f4)/6
end

Runge-Kutta 法を使って、3段法に必要な離散値 $U_2,U_1,U_0, f_2, f_1, f_0$ を返す関数を作ろう

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


function make_init(U)
    V = copy(U)
    sq_V = copy(U)
    sq_f = f(U)
    
    for n in 1:2
        V = RK(V)
        sq_V = hcat(sq_V, V)
        sq_f = hcat(sq_f, f(V))
    end
    
    return sq_V, sq_f
end 

さて、まずは「真の」初期値を適当に用意しよう．

1

U0 = [1.0, 1, 1]

3-element Array{Float64,1}: 1.0 1.0 1.0

そして、これと上で用意した Runge-Kutta スキームを使って作られる後ろ 2ステップ分の初期値がどうなっているか, 試しに見てみよう．

1

make_init(U0)[1]  # これが $U_0, U_1, U_2$ のはず

3×3 Array{Float64,2}: 1.0 1.01257 1.04882 1.0 1.25992 1.524 1.0 0.984891 0.973114

1

make_init(U0)[2]  # これが $f_0, f_1, f_2$ のはず．

3×3 Array{Float64,2}: 0.0 2.47351 4.75173 26.0 26.0947 26.8224 -1.66667 -1.35062 -0.996567

余計な初期値 2ステップ分の計算はどうやら問題ないようだ．

では、線形多段解法 + 予測子修正子法のプログラムだ． 線形計算なので、線形代数の記号を使うと簡単にかけるはず だと考えて書こう．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


function LM(U, vF) # vF = Fn, Fn-1, Fn-2 のつもり．
    
    # Predictor
    Up = U + Δt * ( vF * [23/12, -4/3, 5/12] )
    # Evaluator
    fp = f(Up)
    # Corrector
    Up = U + Δt * ( hcat(fp, vF) * [3/8, 19/24, -5/24, 1/24] )
    # Evaluator
    fp = f(Up)
    
    return Up, hcat(fp, vF[:,1:2]) # 入力と同じ型のデータで更新したものを返す
end  

早速、計算してみよう

1
2
3
4
5
6
7
8
9


sq_U, sq_f = make_init(U0) # 初期値を作成．

U = sq_U[:,3]
vF = copy(sq_f)

for i in 1:3000
    U, vF = LM(U,vF)
    sq_U = hcat(sq_U, U)
end

試しに結果の数字をちょろっと見てみる．

1

sq_U

3×3003 Array{Float64,2}: 1.0 1.01257 1.04882 1.07379 1.16296 … 2.87227 2.31572 1.8142 1.0 1.25992 1.524 1.78498 2.07339 -2.97887 -2.9685 -2.93744 1.0 0.984891 0.973114 0.959705 0.957358 29.1586 28.3153 27.5102

あまり変なことにはなっていなさそうなので、プロットしてみよう．

1
2
3
4
5
6
7
8


using Plots

default(fmt = :png)
# 描画点が多く、web browser に負荷が大きいので、
# 以降の画像表示形式を png にして負荷を下げておこう

t_sq = Δt * [1:3003]
plot(t_sq, sq_U') 

png

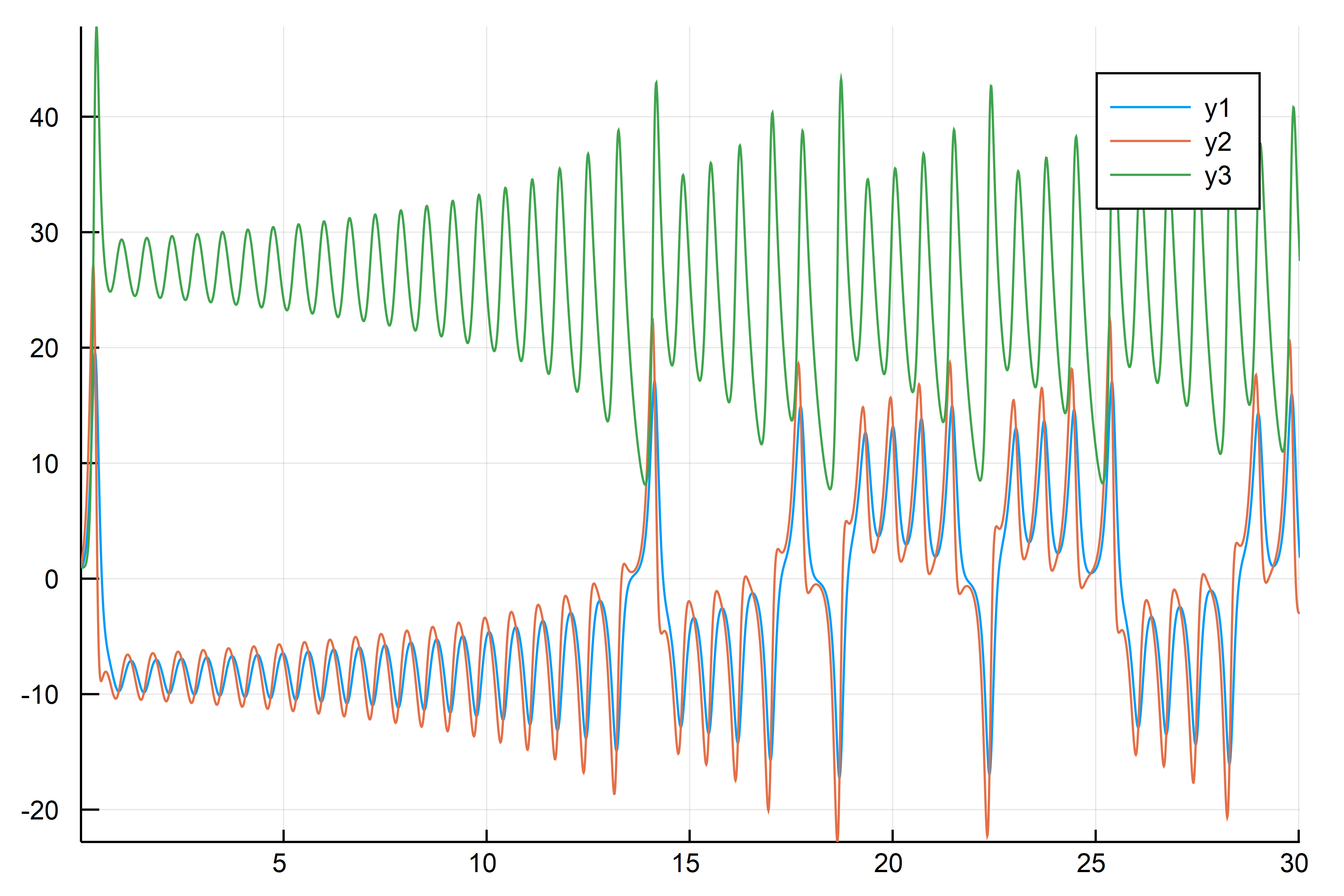
大丈夫そうだ．では、相図にして見てみよう．

1
2


X, Y, Z = sq_U[1,:], sq_U[2,:], sq_U[3,:]
plot(X, Y, Z)

png

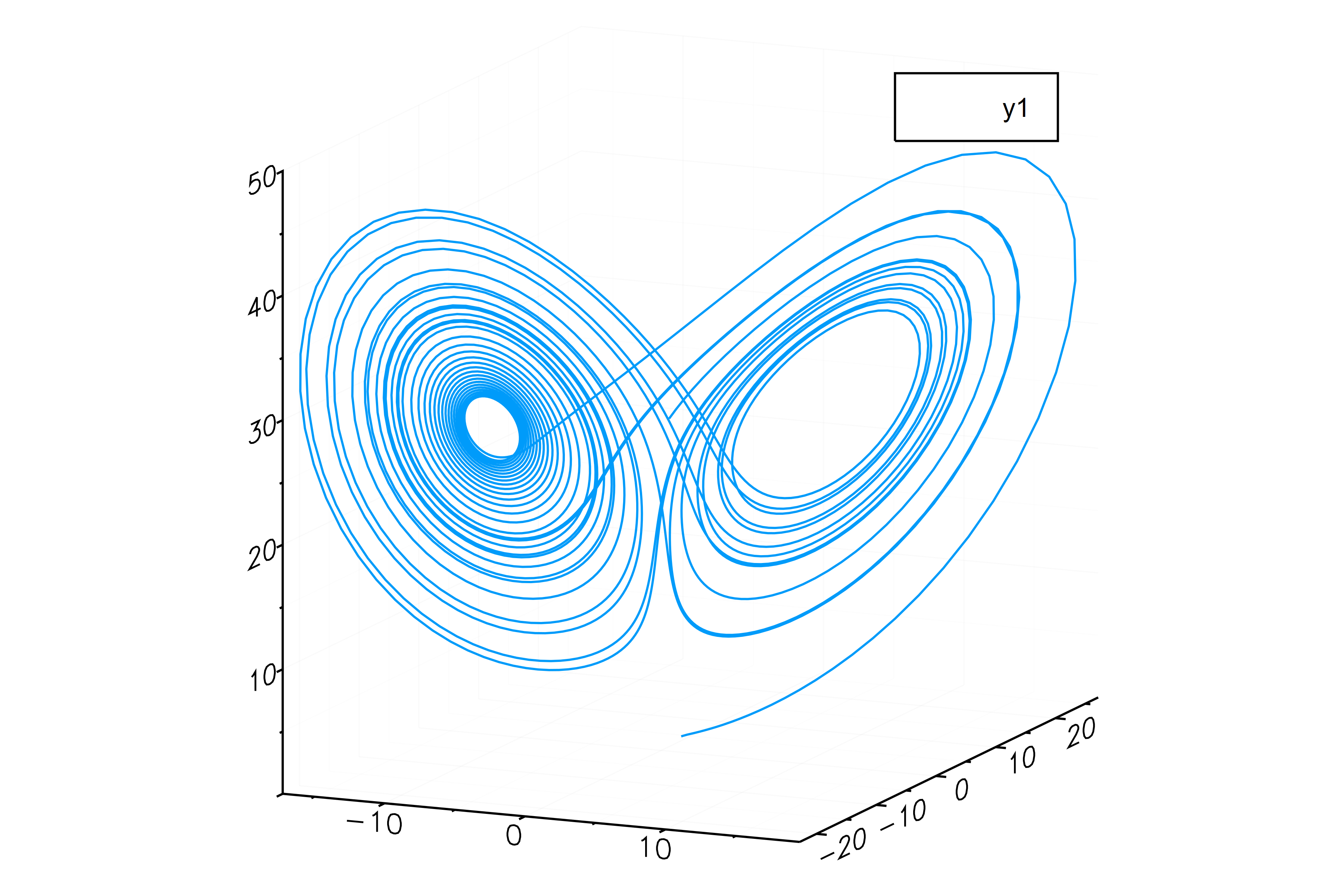
おお、大丈夫そうだな．それにしてもこの相図は興味深い．調べてみよう(課題へ)

せっかくなので、全プロセスを Runge-Kutta 法で計算した場合でも似たような結果になることを確かめておこう．

1
2
3
4
5
6
7


U = copy(U0)
sq_U = copy(U)

for i in 1:3002
    U = RK(U)
   sq_U = hcat(sq_U, U)
end

1

plot(t_sq, sq_U')

png

1
2


X, Y, Z = sq_U[1,:], sq_U[2,:], sq_U[3,:]
plot(X, Y, Z)

png

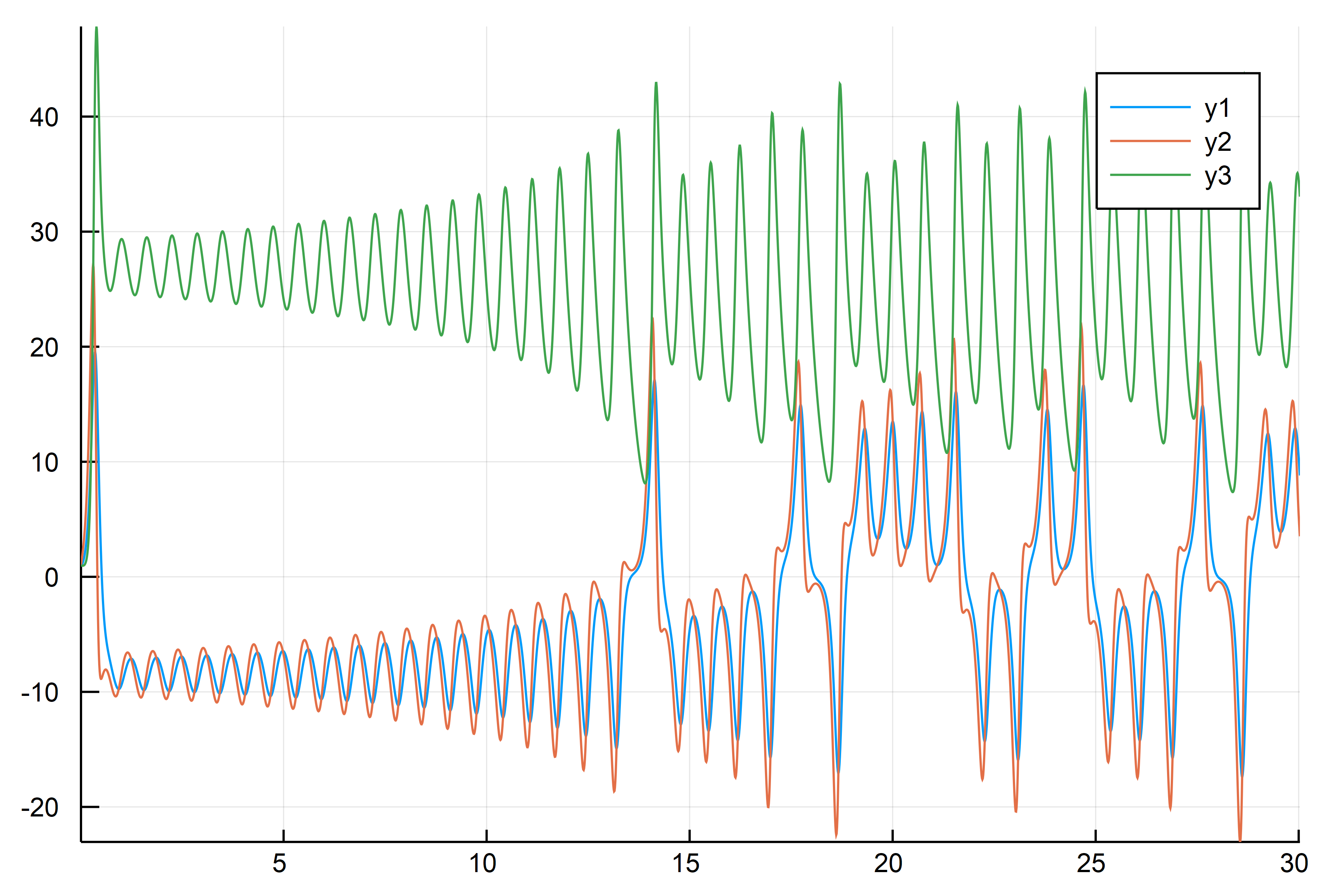
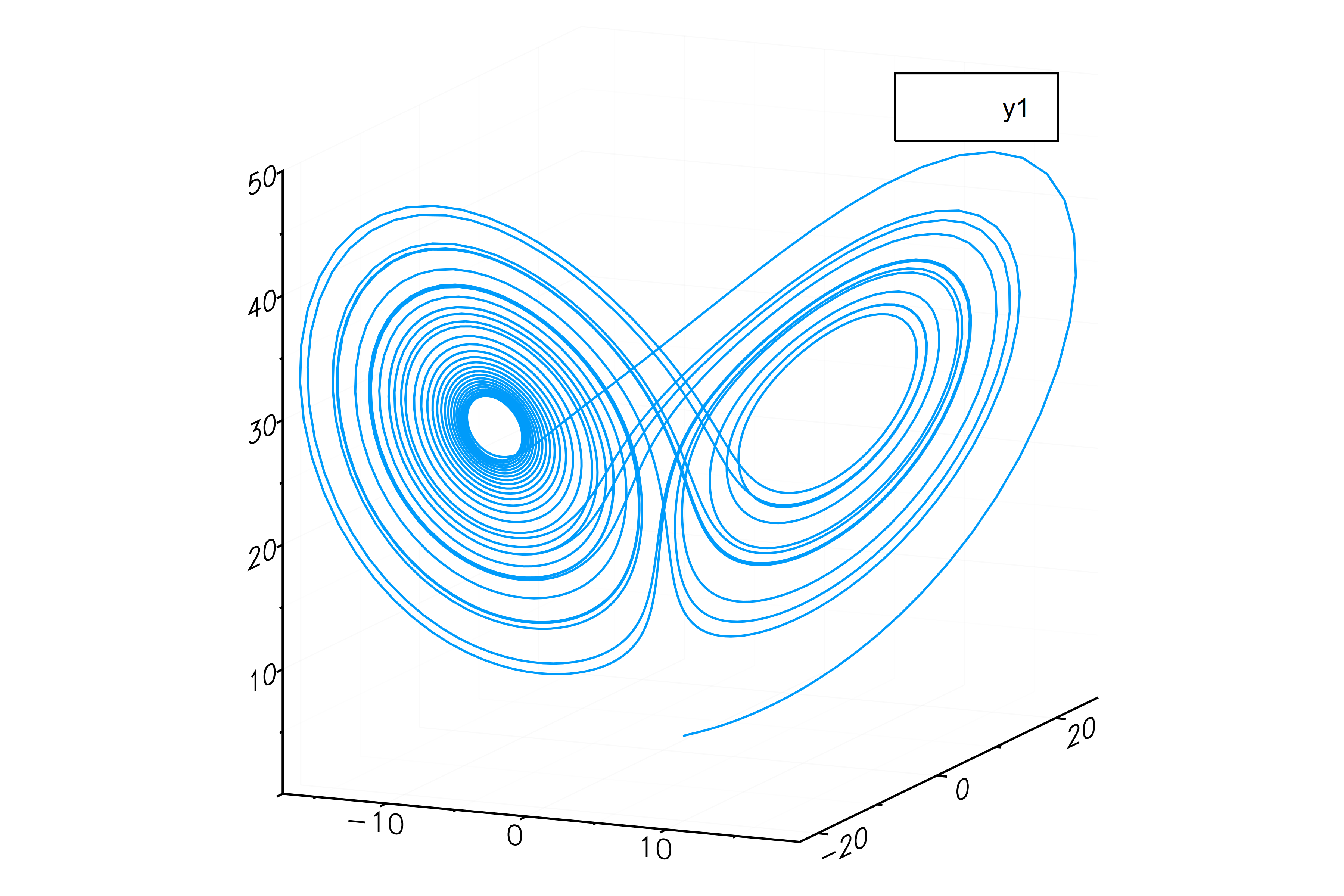
ふむ、どうやらどちらも計算結果は悪くはなさそうだ．しかし、結果は微妙に異なっていることにも留意しておこう．

Runge-Kutta法との速度比較をしてみよう

まず、初期値をいれたら最後の解を出力する形で両方の関数を作ろう．

まずは Runge-Kutta 法だ．

1
2
3
4
5
6
7
8
9


function RKout(init_U, N) # 初期値と最終ステップ数だけを与えれば良いとしよう．
    U = copy(init_U)

  for i in 1:N-1 # 正確には、これで最終ステップが N になる
    U = RK(U)
  end
    
    return U
end

次に線形多段階法だ．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


function LMout(init_U, N) # 初期値と最終ステップ数だけを与えれば良いとしよう．
    sq_U, sq_f = make_init(init_U) # 初期値を作成．Runge-Kutta が2回動作する．
    U = sq_U[:,3]
    vF = copy(sq_f)

    for i in 1:N-3  # 正確には、これで最終ステップが N になる
      U, vF = LM(U,vF)
    end

    return U
end

試しに一度両方動かしてみよう．値そのものはだいぶ違ってくることがわかる．

1

RKout(U0,3000)

3-element Array{Float64,1}: 10.380754908974236 5.336383001817612 34.48595477125319

1

LMout(U0,3000)

3-element Array{Float64,1}: 3.486917444133642 -2.9574191177496814 30.042166580039385

では、両方の速度を測ってみよう．それには、BenchmarkTools というパッケージに入っている、@benchmark というマクロが便利だ．

1
2


using BenchmarkTools 
# 使う準備をする．インストールしてない人は、インストールしよう．

まずは Runge-Kutta 法の速度を見よう．

1

@benchmark RKout(U0,10000)

BenchmarkTools.Trial: memory estimate: 19.07 MiB allocs estimate: 229978 -————- minimum time: 26.398 ms (0.00% GC) median time: 31.437 ms (12.88% GC) mean time: 31.220 ms (11.49% GC) maximum time: 36.891 ms (13.84% GC) -————- samples: 161 evals/sample: 1

次は線形多段解法の速度だ．

1

@benchmark LMout(U0,10000)

BenchmarkTools.Trial: memory estimate: 16.02 MiB allocs estimate: 160019 -————- minimum time: 12.069 ms (0.00% GC) median time: 16.468 ms (22.00% GC) mean time: 15.901 ms (17.73% GC) maximum time: 20.244 ms (29.47% GC) -————- samples: 315 evals/sample: 1

ふむ、理論的には微分値 $f(t,u)$ の評価回数が半分の線形多段解法が有利で、実際に計算時間もそうなっているようだ． Runge-Kutta 法と同様の結果が得られて計算速度が倍早いとなれば、これはなかなか良いのではないか．

プログラミング経験が多少ある人へ…

通常の言語によるプログラミング経験がある人だと、上の LM 関数は無駄が多くて遅いじゃん！と思うかもしれない．まあそういう側面はあるかもしれない．

でも、Julia ぐらいになるとコンパイラが相当に優秀で最適化を頑張ってくれるので、普通に思うよりも無駄の影響は小さかったりするし、無駄を排除すると、今度はプログラムが読みにくくなったり、エラーに弱くなったりする．なので、プログラムの最適化/高速化は、プログラム開発の「最後にやろう」．

ともあれ、無駄だと思わせる一部分を改善した次の関数 LM2 を使って, もとの LM より計算速度がどれくらい改善されるか見てみよう．

ちなみに、下で使っている @inbounds という命令は、配列の添字アクセスがはみ出てないかのエラーチェックを「しない」という命令だ．少しだけ計算が早くなるが、プログラムが完成してないうちは使わないほうがいいなあ…

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


coeff1 = Δt * [23/12, -4/3, 5/12] # 一回計算すれば良いようにして無駄を排除した…
coeff2 = Δt * [3/8, 19/24, -5/24, 1/24] # 同上

function LM2(U, vF) # vF = Fn, Fn-1, Fn-2 のつもり．
    
    # Predictor
    @inbounds Up = U + vF * coeff1
    # Evaluator
    fp = f(Up)
    # Corrector
    @inbounds Up = U + hcat(fp, vF) * coeff2
    # Evaluator
    fp = f(Up)
    
    @inbounds return U, hcat(fp, vF[:,1:2]) # 入力と同じ型のデータで更新したものを返す
    end  

function LM2out(init_U, N) # 初期値と最終ステップ数だけを与えれば良いとしよう．
    sq_U, sq_f = make_init(init_U) # 初期値を作成．Runge-Kutta が2回動作する．
    U = sq_U[:,3]
    vF = copy(sq_f)

    for i in 1:N-3  # 正確には、これで最終ステップが N になる
      U, vF = LM2(U,vF)
    end

    return U
end

まず、動くかどうか試そう．

1

LM2out(U0, 10000)

3-element Array{Float64,1}: 1.0488237097089568 1.5239971313226008 0.973114219876485

ふむ、動くは動くようだな．では、肝心の計算速度はどうかな？

1

@benchmark LM2out(U0, 10000)

BenchmarkTools.Trial: memory estimate: 11.75 MiB allocs estimate: 120031 -————- minimum time: 10.259 ms (0.00% GC) median time: 13.647 ms (20.56% GC) mean time: 13.054 ms (14.23% GC) maximum time: 24.336 ms (19.04% GC) -————- samples: 383 evals/sample: 1

この改善したプログラムだと、もとの線形多段階法のプログラムに比べておおよそ 2割程度のスピードアップが見込めるようだね．必要なメモリ容量も少なくて済んでいるみたいでいい感じだ．

あとは、関数 $f$ の計算が「大変になればなるほど」、この線形多段解法の計算の方が速くなるはずだ．

Report No.08 Lorenz 方程式について…

なんらかの資料を探して、Lorenz 方程式の数学的な特徴を調べて報告せよ．とくに、数値計算の結果の良し悪しをチェックするのに役に立ちそうな特徴について詳しく調べよう．
Lorenz 方程式の相図上での近似解の動きを動画にしてみよう