さて,前回はロジスティック写像によって変化していく数列の挙動が,
パラメータ R によって大きく変わるという現象について調査を行った.
今回はその続きを行ってみよう.
ロジスティック写像の式だけ再掲すると,
(ロジスティック写像) vn+1 = R vn (1-vn)
である.
→ Mathematica での計算の道具として,前回作成 & 用いた
Logistic[R_, v_] := R * v * (1 - v) // N[#, 200] & ← 今回は精度を200桁にあげてみよう.
LAddList[R_, list_] := Append[list, Logistic[R, list[[-1]] ] ]
LogisticList[ini_, R_, ite_] := Nest[LAddList[R, #]&, {ini}, ite]
LogisticPlot[ini_, R_, ite_] := Module[{plotob},
plotob = LogisticList[ini, R, ite];
ListPlot[plotob, PlotJoined -> True, PlotRange -> {0, 1}];
Return[plotob];
]
Nround[r_, a_] := Round[r*(10^a)] / (10^a)
LogisticLimit[initial_, R_] := Module[{plotob, takenum, takelist, iteration},
iteration = 500;
takenum = 200; ← 今回は200点とってより精密なグラフに.
plotob = LogisticList[initial, R, iteration];
takelist = Take[plotob, -takenum] // Nround[#, 3]& // N // Union; ← 今回は思い切って3桁で丸めている
Return[Table[{R, takelist[[n]]}, {n, 1, Length[takelist]}]];
]
LogisticLimitGraph[initial_, Rmin_, Rmax_] := Module[{takelist, iteration, dR},
iteration = 400; ← 今回は400分割してより精密なグラフに.
dR = (Rmax - Rmin)/iteration;
takelist = Flatten[Table[LogisticLimit[initial, (dR*n)+Rmin ], {n, 0, iteration}], 1] ;
ListPlot[takelist, PlotRange -> All, PlotStyle -> PointSize[0.001]]; ← 今回はより小さい点で表示
Return[takelist];
]
という関数7つを用いるので,Mathematica に入力しておくこと.
(赤字は前回に対しての変更部分である)
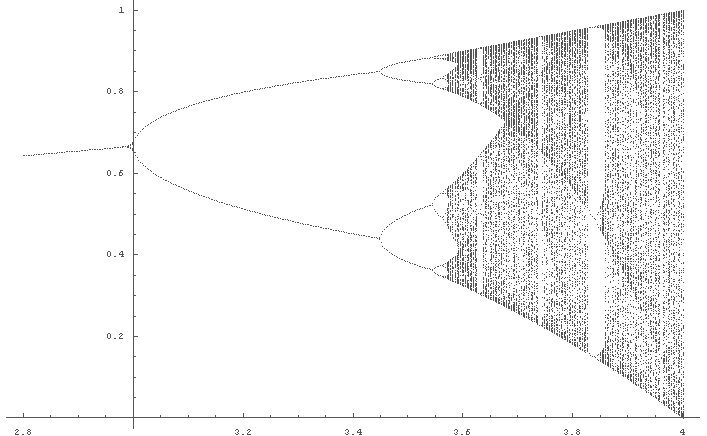
さて,ためしにまずより細かくなった全体図を見てみよう.
In[1]:= LogisticLimitGraph[0.2, 2.8, 4]; ← 前回より細か細かい分,だいぶ計算時間がかかる

前回の粗いグラフに比べるとだいぶ細かくなり,さらにいろいろなことが言えそうだ.
例えば,細かくなったおかげで次のようなことが言える.
■ 仮説 1
R > R2 (ただし R2 は 3.5 付近?) の領域でも,
ロジスティック写像による数列がいくつかの値に収束する=「でたらめでない」
部分が複数ある.
(授業中の課題)
→ いくつあるか. グラフから数えてみよ.
(授業中の課題)
→ それらの R はおよそいくつか.マウスカーソルを用いてグラフ上の座標を調べる方法(以前やった)を用いて調べよ.
(授業中の課題)
→ それらの R の時,ロジスティック写像によって変化する数列は実際にはどのようか.
実際にその R で計算してみて目で確かめよ.
われわれが以前「でたらめさ」を少し考察したとき,
"われわれが「でたらめ」と思うのは,どうやら vn
が n → ∞ で非常に多くの値になる,ということではないだろうか?"
と考えた.
これは上のグラフで言えば,「目で見て黒っぽいところ」として認識される.
これをなんとかよりわかりやすくできないだろうか?
これは,要するに
"vn が n → ∞ でとる値の「個数」を調べる"
ことであるので,そういう関数を作ってみよう.
まず,LogisticLimit がちょうど
"vn が n → ∞ でとる値のリスト"
であるので,この結果の「個数」を調べる関数
LogisticLimitN[iniatial, R]
というのを作ってみよう.
(授業中の課題)
→ LogisticLimitN を作れ. … (ヒント) リストの要素の個数を数えるには?
その LogisticLimitN を使ってみると,次のようになるはずだ.
In[2]:= LogisticLimitN[0.2, 2.8]
Out[2]= 1 ← "vn → 一定値" を意味する.
In[3]:= LogisticLimitN[0.2, 3.5]
Out[3]= 4 ← "vn → 4つの値に落ち着く=(周期的な)変化" を意味する.w
In[4]:= LogisticLimitN[0.2, 4]
Out[4]= 165 ← "事実上でたらめ" を意味する?
さて,この LogisticLimitN を用いて,R を変えたときに, vn が(n→∞で) いくつの値をとるかを見るとすると, 次のような関数を作ればよいだろう.
In[5]:= LogisticLimitNum[initial_, Rmin_, Rmax_] := Module[{takelist, iteration, dR},
iteration = 400;
dR = (Rmax - Rmin)/iteration;
takelist = Table[{(dR*n) + Rmin, LogisticLimitN[initial, (dR*n) + Rmin]}, {n, 0, iteration}];
ListPlot[takelist, PlotRange -> {0, Automatic}, PlotJoined -> True, PlotStyle -> PointSize[0.001]];
Return[takelist];
]
すると,
In[6]:= LogisticLimitNum[0.2, 2.8, 4];
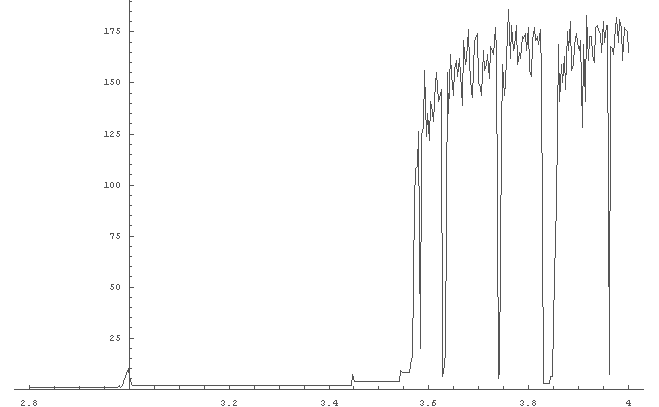
が得られる.
このグラフと先のグラフをあわせて考えれば,これまでの仮説が直感的に理解できるだろう.
(授業中の課題)
→ 仮説 1 はこのグラフではどう解釈することになるか.
(授業中の課題)
→ このグラフで仮説 1 を検証し,先のグラフで調べた結果と比較せよ.
□ レポート課題 1
前回のレポート課題 5 をこの関数 LogisticLimitNum を駆使してやり直してみよ.
さて,われわれは直感的に感じた「でたらめさ」というものの正体にせまるべくいろいろ調べているわけだが,
ここで少し視点を変えてみよう.
われわれの生活の中にあるでたらめなもの,を探してみて,それとの比較,
アナロジーとして使えそうなものはないだろうか…
と考えて思いつくのは「音」である.
われわれがなんとなく「雑音」と呼んでいるものは「でたらめ」という意味で関係ないのだろうか.
そこで,ロジスティック写像によって得られる数列を「音」として聞いてみよう.
これによって「でたらめさ」を理解する手がかりが増えるかもしれない.
リストを音として聞くには,以前用いた ListPlay が使えるので,それを用いて,
LogisticSound[initial, R, iteration] という関数を作ってみる.
In[7]:= LogisticSound[ini_, R_, ite_] := Module[{plotob},
plotob = LogisticList[ini, R, ite];
ListPlay[plotob, SampleRate -> ite]; ← ちょうど 1秒間音がなるようにしてある.
Return[plotob];]
In[8]:= LogisticSound[0.2, 3.2, 1000]; ← 1000個ぐらいの数列は必要だろう
← 普通の単音(に近い音)が聞こえる.
In[9]:= LogisticSound[0.2, 3.5, 1000]; ← やはり普通の単音(に近い音)が聞こえる.
In[10]:= LogisticSound[0.2, 3.8, 1000]; ← さて?
In[11]:= LogisticSound[0.2, 3.84, 1000]; ← さて?
In[12]:= LogisticSound[0.2, 4.0, 1000]; ← さて?
さて,どうだっただろうか.
スピーカの質などによって聞き取りにくいかもしれないが,この結果は
数列を音として聞くことによって「数列がでたらめかどうか」判断できる可能性がある
ことを意味している.
つまり,「目で見る」方法の他に,「耳で聞く」という手段も(直感的な意味で)使えるということである.
ここで音を「解析」する方法の一つとして Fourier 展開,Fourier 変換があったことを思い出す!
たとえば,ロジスティック写像による数列を Fourier 変換する関数 LogisticFourier[初期値, R, 点数] というのを作ったとして,
… →授業中の課題
In[13]:= LogisticFourier[0.2, 3, 1000]
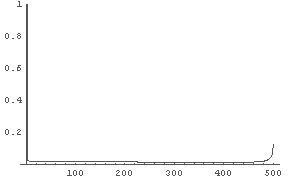 ← R=3 の時の数列の(離散) Fourier 変換の結果
In[14]:= LogisticFourier[0.2, 3.5, 1000]
← R=3 の時の数列の(離散) Fourier 変換の結果
In[14]:= LogisticFourier[0.2, 3.5, 1000]
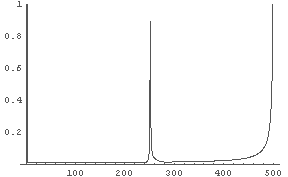 ← R=3.5 の時の数列の(離散) Fourier 変換の結果
In[15]:= LogisticFourier[0.2, 3.7, 1000]
← R=3.5 の時の数列の(離散) Fourier 変換の結果
In[15]:= LogisticFourier[0.2, 3.7, 1000]
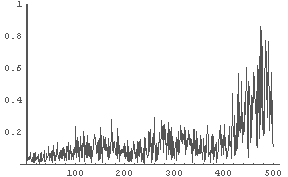 ← R=3.7 の時の数列の(離散) Fourier 変換の結果
In[15]:= LogisticFourier[0.2, 3.83, 1000]
← R=3.7 の時の数列の(離散) Fourier 変換の結果
In[15]:= LogisticFourier[0.2, 3.83, 1000]
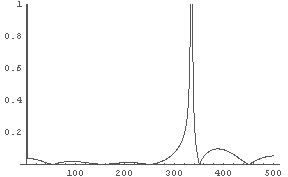 ← R=3.83 の時の数列の(離散) Fourier 変換の結果
In[15]:= LogisticFourier[0.2, 4, 1000]
← R=3.83 の時の数列の(離散) Fourier 変換の結果
In[15]:= LogisticFourier[0.2, 4, 1000]
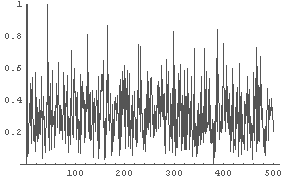 ← R=4 の時の数列の(離散) Fourier 変換の結果
← R=4 の時の数列の(離散) Fourier 変換の結果
R を変えると数列の Fourier 変換の結果があきらかに変わるのが分かるだろう.
では,この結果と「でたらめさ」には何か関係があるだろうか?
(授業中の課題) → 確かめてみよ.
値の大きさにも注意してこの実験の結果を慎重に検討することによって次のような仮説がたてられるだろう.
■ 仮説 2
でたらめな数列を(離散) Fourier 変換すると,値は全周波数領域にかなり「均等に」散らばる.
また,でたらめでない数列を変換すると,鋭いピークがいくつかたつという形状になる.
= 「でたらめさ」の中身へのとっかかり その2
→ さらに,周波数領域への散らばり方の均等さ加減を数量化することで,
「でたらめさの度合いを数量化できる」可能性があることにも注目せよ.
□ レポート課題 2
仮説 2 が正しいかどうか,実験を通じて検証せよ.
□ レポート課題 3
仮説 2 が正しいかどうか,(理論的な)考察を行え.
□ レポート課題 4
仮説 2 が正しいとして,でたらめさを数量化するにはどうしたらよいだろうか.
考察してみよ.
□ レポート課題 5
音として聞くと,なぜ「でたらめな」数列とそうでない数列を区別できるのだろうか.
仮説 2 が正しいと仮定して考えよ.
ロジスティック写像による数列のグラフを見て「でたらめ」と感じたのは,
「初期値がわかっていても n→大 で vn がいくつになるか全く予想できないのでは?」
という疑問を感じたから,というのも理由の一つであろう.
しかし,ロジスティック写像そのものはごく簡単な漸化式であり,
vn-1 がわかっているならば vn は厳密に分かる.
近くが厳密に分かるならば,それを繰り返すことで遠くも厳密に分かるはず,
というのが理論的な考え方というものである.
それはこのロジスティック写像の場合も全く正しい.
きちんとした計算を重ねることで,いくらでも大きな n に対して
vn の値を求めることが原理的に可能だからだ.
にもかかわらず,われわれがロジスティック写像の数列グラフから感じたのは
「(n が)近い時の挙動はよく分かるが,遠くなると全く予想できない(ように感じる)」ということであり,
これは明らかに何か「変な点」がある.
これをもう少しだけきちんとした用語を使っていうと,
vn-1 → vn
という局所的(local)な挙動は分かるが
v0 → vn (n は大)
という大域的(global)な挙動は全く予測できない
ということであり(これを大域的予測不可能性ということもある),
ここに大事なものが隠れていそうだ,ということである.
この理論的な「奇妙さ」について何かわかることがあれば,それはまた
「でたらめさ」について知る手がかりとなるだろう.
そこで,この「大域的な予測不可能性」について調べてみよう.
大域的な予測について調べるので, R=4, n=100 とひとまず固定して調べてみよう.
で,R=4 の時に初期値 v0 から v100 が予測できるかどうか試してみるのである.
ロジスティック写像による数列の最後の値はリストの要素を抜き出す作業だから
LogisticList[初期値, R, 個数][[-1]]
で得られる.
ではいくつか計算してみよう.
In[16]:= LogisticList[0.1, 4, 100][[-1]]
Out[16]= 0.372447
In[17]:= LogisticList[0.2, 4, 100][[-1]]
Out[17]= 0.875591
In[18]:= LogisticList[0.3, 4, 100][[-1]]
Out[18]= 0.673899
In[19]:= LogisticList[0.4, 4, 100][[-1]]
Out[19]= 0.240613
…以下,略…
これらの結果から,初期値 v0 から v100 が予想できるだろうか?
少なくとも,このいくつかの数字からはなんらかの脈絡は見いだせない.
そこで,例によってグラフを描いてみることにしよう.
初期値をいくつか変えて,ロジスティック写像による最終結果をプロットする関数を
LogisticInitGraph[R, n の最終値, 最小初期値, 最大初期値]
とするとして,
In[20]:= LogisticInitGraph[R_, ite_, IniMin_, IniMax_] := Module[{dIni, IniIte, takelist},
IniIte = 400; ← 初期値を401通り変えて計算することに.
dIni = (IniMax - IniMin)/IniIte;
takelist = Table[{IniMin + n*dIni, LogisticList[IniMin + n*dIni, R, ite][[-1]]}, {n, 0, IniIte}];
ListPlot[takelist, PlotJoined -> True];
Return[takelist];
]
と関数を作ってみる. すると,
In[21]:= LogisticInitGraph[4, 100, 0.1, 0.2];
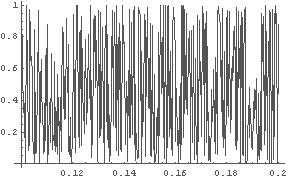 ← 初期値 0.1 〜 0.2 の時の最終結果 v100
← 初期値 0.1 〜 0.2 の時の最終結果 v100
これまた「でたらめ」である(^-^;)
もしかして 0.1 〜 0.2 ととった初期値の幅が広すぎたのかもしれない,
と考えてより細かい範囲で計算してみると…
In[22]:= LogisticInitGraph[4, 100, 0.1, 0.11];
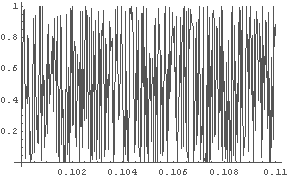 ← 初期値 0.1 〜 0.11 の時の最終結果 v100
In[23]:= LogisticInitGraph[4, 100, 0.1, 0.101];
← 初期値 0.1 〜 0.11 の時の最終結果 v100
In[23]:= LogisticInitGraph[4, 100, 0.1, 0.101];
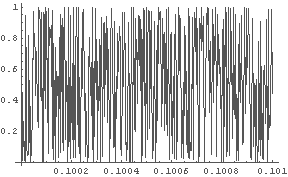 ← 初期値 0.1 〜 0.101 の時の最終結果 v100
In[24]:= LogisticInitGraph[4, 100, 0.1, 0.1001];
← 初期値 0.1 〜 0.101 の時の最終結果 v100
In[24]:= LogisticInitGraph[4, 100, 0.1, 0.1001];
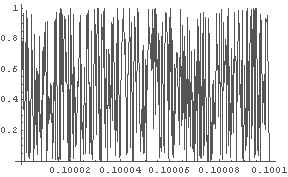 ← 初期値 0.1 〜 0.1001 の時の最終結果 v100
← 初期値 0.1 〜 0.1001 の時の最終結果 v100
と,どこまで細かく見てみてもでたらめである.
これは言い換えると初期値が「ほんのちょっと変わるだけで vn は全然違う値になり,しかもその値は予測できない」
ということである.
(これを「初期値敏感性」とか「初期値鋭敏依存性」とかいったりする).
,この結果として,初期値と vn とを結び付ける(予測する)ことが出来ない,ということがいえそうだ.
つまり,次のことが仮説として言えそうである.
■ 仮説 3
初期値が「微少に」異なった場合,ロジスティック写像による数列は(n
がいくらか進むと)全く異なるものとなる.
そして,これが実質的な「大域的な予測不可能性」の原因である.
= 「でたらめさ」の中身へのとっかかり その3
(授業中の課題)→例えば初期値 = 0.1 の時の数列のグラフと, 初期値 = 0.1001
の時の数列のグラフを色違いで重ねてみて,その違いを見てみよ.
□ レポート課題 6
様々な初期値, R にたいして実験を行い,仮説 3 を確かめよ.
□ レポート課題 7
仮説 3 について理論的な考察,説明を行え.
(難しいと思ったら無理しなくてよい)
ここまでわれわれはロジスティック写像の数列の発展の様子を通じて,様々な現象や概念,考え方を見てきた.
しかし,これらの現象や概念はロジスティック写像だけのものではない.
現実世界ではむしろかなり普遍的なものである,と認識した方が良いだろう.
そういう意味では,これらの話の流れ,をよくよく理解しておくとよい.
(なんとなれば,Mathematica の操作は全くできなくても…)
□ レポート課題 8
これまでロジスティック写像に対して行った様々な実験,仮説の構築,検
証等を,第 8 回の問い7 の関数 f に対して行ってみよ.
さて,初期値敏感性や大域的予測不可能性,そしてそれらを内包するカオスは
「科学する」にあたって一見困った現象のように思える.
しかし,これらは
「未来の決定性問題」「自由意思の存在問題」「プログラム停止問題」
「セルオートマトンの発展予測問題」「全知全能性の限界」
「進化論(カオスの縁説)」
などと根本で深く結び付く.
つまり,
これらの現象は,われわれ人類にとって(科学,思想,哲学あらゆる意味で)本質的な一部分をなすもの
であり,けして無視することのできない存在である.
文系であっても,いや,文系だからこそこれらの現象について何も知らないというのは許されまい…
(→ こうした道草的話はまたどこかで(^-^))