さて,前回は簡単な微分方程式二つについて,微分方程式を離散近似し,
離散近似の Δt → 0 の極限 は微分方程式に相当するという期待
をもとに簡単な考察を加えてみた.
そこで今回はちょっと目先を変えて,Δt → 大 の時は離散近似に何が起こるか見てみよう.
これは,
→ 微分方程式からは離れ, 漸化式の世界に近づく.
→ よく考えると,昼夜で条件が大きく変わる気象現象,
夏冬でやはり条件が大きく変わる生物世界などでは,
現象自体が「漸化式」の世界により近い.
→ 自然現象の中には微分方程式よりもこうした「漸化式」で考えるべき
ものが多くあるはず.
という立場に立ち,漸化式についても調べておくべきことがあるだろう,考えるものである.
ついでにいえば,
滑らかでない世界ではどんな奇妙なことが起こるか,
その一端も垣間見ようというムシのいい話,でもある.
ロジスティック写像
前回導入したロジスティック写像を今回の調査対象として用いてみよう.
式だけ再掲すると,
(ロジスティック写像) vn+1 = R vn (1-vn), R := 1 + rΔt
である.
この式の詳細については前回の話を参照してもらうとして,
大雑把にいうならば,
vn 匹の生物が増減して vn+1 匹になる
様子を示した式と思えばよい.
(他にも適用例は沢山ありそうだ.
例えば,vn = 第 n 代目の○○家の財産とか…)
→ Mathematica での計算の道具として,前回用いた
Logistic[R_, v_] := R * v * (1 - v) // N[#, 150] &
LAddList[R_, list_] := Append[list, Logistic[R, list[[-1]] ] ]
という関数を用いるので,Mathematica に入力しておくこと.
さて,初期値 v0 から出発してロジスティック写像に基づいて
一つずつ真面目に v0 → v1 → v2 → v3 → …
と計算していくにはどうしたか思い出すと,例えばR=2, v0 = 0.2 の場合は次のようにしたのだった.
In[1]:= Nest[LAddList[2, #]&, {0.2}, 100]; ← v1, ..., v100 を求めている.
In[2]:= ListPlot[%, PlotJoined -> True] ← 結果をグラフ表示.
毎回 Nest 命令を書き込むのは面倒なので LogisticList[初期値, R,
求める点数] という関数を次のように定義して使おう.
ついでに,グラフ化してしまう命令も LogisticPlot[初期値, R, 求める点数]
として作っておこう.
In[3]:= LogisticList[ini_, R_, ite_] := Nest[LAddList[R, #]&, {ini}, ite]
← 初期値が ini, ロジスティック写像のパラメータを R, 求める点の数を ite として,
← v1, ..., vite を求めている.
In[4]:= LogisticList[0.2, 4, 100]; ← 初期値 0.2, R=4, 点数=100 で計算してみて,
In[5]:= ListPlot[%, PlotJoined -> True] ← 結果をグラフ表示.
Out[5]= …略…
In[6]:= LogisticPlot[ini_, R_, ite_] := Module[{plotob},
plotob = LogisticList[ini, R, ite];
ListPlot[plotob, PlotJoined -> True, PlotRange -> {0, 1}];
Return[plotob];
] ← 単に上の [3],[5] をまとめただけ.
念の為,計算した結果が Return で確実に取り出せるようにしてある.
In[7]:= LogisticPlot[0.2, 4, 70] ← 初期値 0.2, パラメータR=4, 点数=70 で計算してみると
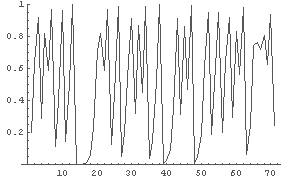 Out[7]= {0.2, 0.64, 0.9216, 0.289014, 0.821939, 0.585421, 0.970813, 0.113339,
0.401974, 0.961563, 0.147837, 0.503924, 0.999938, 0.000246305, 0.000984976,
0.00393603, 0.0156821, 0.0617448, 0.23173, 0.712124, 0.820014, 0.590364,
0.967337, 0.126384, 0.441645, 0.986379, 0.053742, 0.203415, 0.64815,
0.912207, 0.320342, 0.870893, 0.449755, 0.989902, 0.0399856, 0.153547,
0.519882, 0.998419, 0.00631451, 0.0250985, 0.0978744, 0.35318, 0.913776,
0.315159, 0.863335, 0.47195, 0.996853, 0.0125495, 0.0495681, 0.188445,
0.611733, 0.950063, 0.189772, 0.615035, 0.947067, 0.200523, 0.641254,
0.920189, 0.293764, 0.829868, 0.56475, 0.98323, 0.0659554, 0.246421,
0.742791, 0.76421, 0.720773, 0.805037, 0.62781, 0.934659, 0.244287}
← 数値としての結果も出力されるので安心(^-^).
Out[7]= {0.2, 0.64, 0.9216, 0.289014, 0.821939, 0.585421, 0.970813, 0.113339,
0.401974, 0.961563, 0.147837, 0.503924, 0.999938, 0.000246305, 0.000984976,
0.00393603, 0.0156821, 0.0617448, 0.23173, 0.712124, 0.820014, 0.590364,
0.967337, 0.126384, 0.441645, 0.986379, 0.053742, 0.203415, 0.64815,
0.912207, 0.320342, 0.870893, 0.449755, 0.989902, 0.0399856, 0.153547,
0.519882, 0.998419, 0.00631451, 0.0250985, 0.0978744, 0.35318, 0.913776,
0.315159, 0.863335, 0.47195, 0.996853, 0.0125495, 0.0495681, 0.188445,
0.611733, 0.950063, 0.189772, 0.615035, 0.947067, 0.200523, 0.641254,
0.920189, 0.293764, 0.829868, 0.56475, 0.98323, 0.0659554, 0.246421,
0.742791, 0.76421, 0.720773, 0.805037, 0.62781, 0.934659, 0.244287}
← 数値としての結果も出力されるので安心(^-^).
さてこの道具(LogisticPlot)を使っていろいろ見てみよう.
今回は R → 大 として何が起こるのかを見る,という話なので,そうやっ
てまずは様子を見よう.
R = 1 が微分方程式そのものに相当する,という話だったので, R > 1
で少しずつ大きくしてみよう.
→ つまり,R の最小値としては 1 が適当だ.
次に R をどこまで大きくするかだが,前回の「v と u の関係図」を見ると,v は
0 ≦ v ≦ 1 でしかモデル的には意味がないので,その範囲に v が収まるよ
うな R だけ使うことを考えると,R ≦ 4 であることがわかる.
(なぜなら,v(1-v) = v-v2 の 0 ≦ v ≦ 1 での最大値は 1/4 だから)
→ つまり,R の最大値としては 4 が適当だ.
→ 式だけ眺めずに,理論的,モデル的な背景を考慮にいれて考えるこういうセンスは「理論でも実世界でも」非常に大事だ.
理系文系を問わず,大学を出るまでに是非とも身につけておくこと.
さて, 1 ≦ R ≦ 4 で調べることになったので,0.5 刻みで R を変えてグラフを描いてみる.
In[8]:= LogisticPlot[0.2, 1, 70]; ← まずは R = 1.0 で. 数値出力は見たくないので ; をつけている.
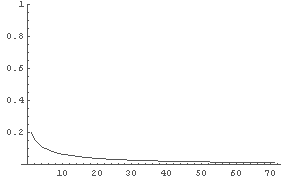 ← R = 1.0: v = ゼロに収束していく?
In[9]:= LogisticPlot[0.2, 1.5, 70];
← R = 1.0: v = ゼロに収束していく?
In[9]:= LogisticPlot[0.2, 1.5, 70];
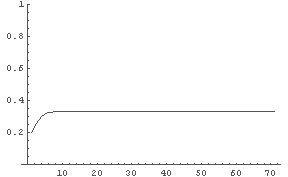 ← R = 1.5: v = 0.3... 辺りに収束か.
In[10]:= LogisticPlot[0.2, 2, 70];
← R = 1.5: v = 0.3... 辺りに収束か.
In[10]:= LogisticPlot[0.2, 2, 70];
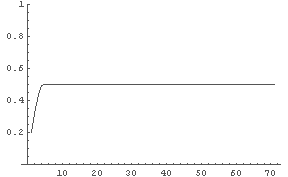 ← R = 2.0: v = 0.5 に収束か.
In[11]:= LogisticPlot[0.2, 2.5, 70];
← R = 2.0: v = 0.5 に収束か.
In[11]:= LogisticPlot[0.2, 2.5, 70];
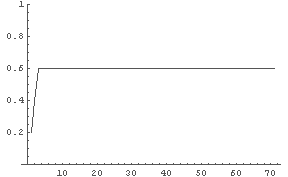 ← R = 2.5: v = 0.6 に収束か.
In[12]:= LogisticPlot[0.2, 3, 70];
← R = 2.5: v = 0.6 に収束か.
In[12]:= LogisticPlot[0.2, 3, 70];
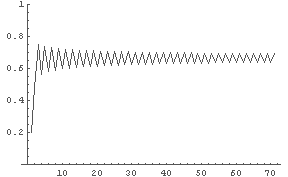 ← R = 3.0: 2つの値の間を振動? ← 判断にはもっと多くの点が必要
In[13]:= LogisticPlot[0.2, 3.5, 70];
← R = 3.0: 2つの値の間を振動? ← 判断にはもっと多くの点が必要
In[13]:= LogisticPlot[0.2, 3.5, 70];
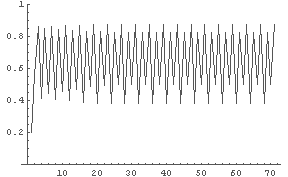 ← R = 3.5: 4つの値の間を振動?
In[14]:= LogisticPlot[0.2, 4, 70];
← R = 3.5: 4つの値の間を振動?
In[14]:= LogisticPlot[0.2, 4, 70];
 ← R = 4.0: でたらめに見える…
← R = 4.0: でたらめに見える…
この簡単なグラフだけからもいくつかのことが推定できる.
それを簡単にまとめて記述すると以下のようになろうか.
■ 仮説 1
ある値 R1 (ただし 2.5 ≦ R1 ≦ 3.0),
R2 (ただし 3.5 ≦ R2 ≦ 4.0),
を境にして R の違いによって,ロジスティック写像による数列の発展の
様子は,t → ∞ で以下のように異なる.
| R |
〜 1 |
1 〜 R1 |
R1 〜 R2 |
R2 〜 4 |
4 〜 |
| 発展の様子(推測) |
(未調査ゆえ不明) |
一定値に収束 |
決まった複数の値で振動 |
一見でたらめ? |
(未調査ゆえ不明) |
なるほど,たった7つのグラフからこれだけのことが推測できる.
だが,とりあえず仮説としたものの,この仮説には考え,調べなければならない点が数多くある.
それをリストアップしてみよう.
特に注意すべきは「でたらめさ」についてである.
なぜなら,これは漸化式の答えを並べたものであるのだから,
「単純な決定された式から複雑なランダムな答えがでてくる?」
という奇妙な推測をわれわれはたてているのだ,ということになるから.
仮説 1 について調べねばならないこと
- ロジスティック写像の計算に精度 150 桁としているが,これが変わっ
ても仮説は成り立つのか?
精度が変わったら R1, R2 の値が変わったりはしないか?
- 初期値として 0.2 を使った例しか調べていない. 初期値が違っても仮説は成り立つのか?
初期値が変わったら R1, R2 の値が変わったりはしないか?
→ 授業中の課題. 初期値を実際に変えてやってみよう.
(以下,仮説1が成り立つとして)
- R1, R2 の値は?
- R = 1 〜 R1 の時の挙動の「一定値」は推測可能か?
- R = R1 〜 R2 の時の挙動の「決まった複数の値」は推測可能か?
- R = R2 〜 4 の時の挙動の「でたらめ」とはどういう意味だろうか?
- R について調べてない範囲では何が起こるだろう?
以下,少しずつ調べていこう.
まず,簡単な部分はレポート課題としてしまう.
□ レポート課題 1
R = 1 〜 R1 の時の挙動の「一定値」は,前回の結果を見ると推測可能なことがわかる.
(Converge 関数を作って云々… という部分である)
それも考慮にいれて,この時の「一定値」はいくつなのか「根拠込みで」示せ.
→ (ヒント) 一定値になるということは,vn+1 = vn になるということだから…
□ レポート課題 2
R1 を実験で求めてみよ.
→ R2 について言えば,「でたらめ」の意味がわかるまではどうしようもないだろう.
□ レポート課題 3
R1 を理論的に求めてみよ.
→ 考え方はやさしいが,無理しなくてもよい(^-^).
□ レポート課題 4
R < 1, R > 4 の時はどういう挙動になるか.
分かる範囲でよいので調べて答えよ.
さて,これらのことを調べるには Mathematica でもう少し工夫しないと不便だ.
そこで,十分多くの点数を計算した段階で vn の値が何なの
か(複数である可能性も考慮して)計算する関数を作ろう.
計算の誤差も考えると重複を適当に除去する関数も欲しいので,まずはそれを作ってから,
LogisticLimit[initial_, R_] という関数を作る.
これは,初期値 initial で パラメータ R としたときに,ロジスティック写像が n → ∞
で大体どういう値をとるかをリストアップする関数である.
In[15]:= Nround[r_, a_] := Round[r*(10^a)] / (10^a) ;
← いったん 10a 倍してから整数で近似して,もとに戻すことによって,
大体 10-a より小さい誤差は無視できるようにする.
まあ,だいたい a 桁の丸めと思えばよい.
In[16]:= LogisticLimit[initial_, R_] := Module[{plotob, takenum, takelist, iteration},
iteration = 500; ← 全部で 500 点計算することにして
takenum = 100; ← 最後の 100 点を出力することに.
plotob = LogisticList[initial, R, iteration]; ← ここでロジスティック写像による数列を計算.
takelist = Take[plotob, -takenum] // Nround[#, 6]& // N // Union; ← 後ろ 100 点を取り出して 6 桁で丸めて重複を除去.
Return[Table[{R, takelist[[n]]}, {n, 1, Length[takelist]}]];
] ← R vs vn を(あるだけ)出力
In[17]:= LogisticLimit[0.2, 1.5]
Out[17]= {{1.5, 0.333333}} ← R = 1.5 だと vn → 0.333333 らしいことがわかる.
上のグラフと比べてみて納得.
In[18]:= LogisticLimit[0.2, 2.0]
Out[18]= {{2., 0.5}} ← R = 2.0 だと vn → 0.5 だ. これも納得.
In[19]:= LogisticLimit[0.2, 3.5]
Out[19]= {{3.5, 0.38282}, {3.5, 0.500884}, {3.5, 0.826941}, {3.5, 0.874997}}
← R = 3.5 とすると vn → (4つの値) となり,これもグラフと合う.
In[20]:= LogisticLimit[0.2, 3.0] ← では R = 3.0 とすると…
Out[20]= {{3., 0.65877}, {3., 0.658779}, {3., 0.658787}, {3., 0.658796},
…略…
{3., 0.67436}, {3., 0.674368}, {3., 0.674376}}
← かなり微妙なようだが,二つの値のようだ.
これ以上荒い丸めはやばそうなので,これ以上は「グラフで目で見て」判断しよう.
とすればよい.ただし,途中で
● 最も近い整数で置き換える(〜四捨五入) … Round[実数]
→ 実数が正の場合は普通の四捨五入.
負の場合は,絶対値に対して四捨五入してから符合を戻すと思えばよい.
を用いている.
これで R (と初期値もだが) を固定したときの n → ∞ での様子を見る関数は作れた.
ただ,微妙なところもあるし,やはり R を変えつつグラフで様子をみるのが良さそうだ.
そこで,R を変えてどうなるか,をグラフで調べるための関数も作ってしまおう.
In[21]:= LogisticLimitGraph[initial_, Rmin_, Rmax_] := Module[{takelist, iteration, dR},
iteration = 200; ← R を 200分割して計算.
dR = (Rmax - Rmin)/iteration;
takelist = Flatten[Table[LogisticLimit[initial, (dR*n)+Rmin ], {n, 0, iteration}], 1] ;
ListPlot[takelist, PlotRange -> All, PlotStyle -> PointSize[0.005]];
Return[takelist];
]
とすればよい.ただし,途中で
● グラフの「点」の大きさを決める … オプション PointSize
→ PointSize[d] とすると,点が直径 d で描かれる.
ただし,サイズはグラフの幅との比となる.
つまり,PlotStyle -> PointSize[0.01] として指定すると,点の大きさはグラフ全体の 1% だ,ということになる.
を用いている.
これで,R の変化で vn (n → ∞) がどうなるかグラフで見える.
ためしに,R1 がどのあたりか見当をつけてみよう.
In[22]:= LogisticLimitGraph[0.2, 2.5, 3.1]; ← R = 2.5 〜 3.1 での v∞ のグラフ.
; をつけて,数列は出力しないようにしている.
計算にはやや時間がかかるので,待つ(^-^).
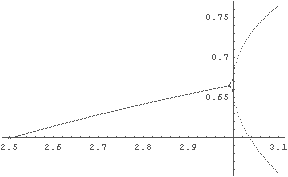 ← お? R1 は 3 付近ということか?
In[23]:= LogisticLimitGraph[0.2, 2.95, 3.05]; ← R = 2.95 〜 3.05 周囲を拡大して計算…
← お? R1 は 3 付近ということか?
In[23]:= LogisticLimitGraph[0.2, 2.95, 3.05]; ← R = 2.95 〜 3.05 周囲を拡大して計算…
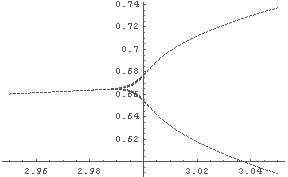 ← R1 はいくつぐらいだ?
← R1 はいくつぐらいだ?
これで多くのことが目で見て判断できそうだ.
(これと同じ作業を手でやることを想像してみよ)
そこで,この LogisticLimitGraph を用いて,全体をはじめから見てみよう.
In[24]:= LogisticLimitGraph[0.2, 1, 4]; ← R = 1 〜 4 での v∞ のグラフ. 全体をまず見てみる.
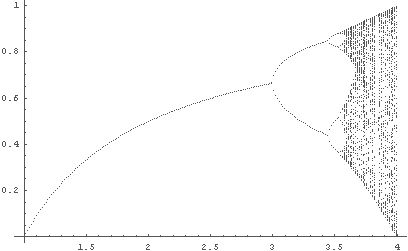
細かいことを見るにはあまりにこのグラフは粗い.
しかし,こんなグラフでさえ,先の仮説 1 とをよく比較してみると
大雑把にであるが全体が少しずつ分かってくる.
つまり,
- R1 は 3 付近だ. ← これは先の「試し」で分かっている.
- R1 と R2 との間にもどうやらいくつもの
「境界値」があって,その値を越えて R が大きくなる度に
vn (n→∞) の値の数がその「2倍」になっていくように見える.
- われわれが「でたらめ」と思うのは,どうやら vn
が n → ∞ で非常に多くの値になる,ということではないだろうか?
= 「でたらめさ」の中身へのとっかかり その1
ただし,多くの値に変化していくその変化のし方が「規則的か」「でたらめに見えるか」
の区別はこのグラフからは分からないので,それについてはまだ何も言えない.
- となると R2 は 3.5 〜 3.7 付近ではないだろうか.
- しかし,R が約 3.8ちょっと の付近で「でたらめでなくなっている」
ようにも見える.
これらのうち,いくつかをきちんと書くと…
■ 仮説 2
R1 (ただし R1 は約 3.0),
R2 (ただし 3.5 ≦ R2 ≦ 3.7),
に対し,
R1 = R1.0 <
R1.1 < R1.2 < R1.3 < ....
< R2 なる特別な値 R1.0, R1.1, R1.2, R1.3,
.... が存在して,
R が R1.x を越えて大きくなる度に
vn (n→∞) の個数が倍になる.
□ レポート課題 5
R1.1, R1.2, R1.3, ...
を分かる範囲でよいので調べよ.
また,それらの値の間に何か関係はないか.
→ R がいくつで v の様子がでたらめになるのか,が推測できる手がかりになるかも.
■ 仮説 3
R = 3.8 付近では,ロジスティック写像による数列はでたらめでない.
□ レポート課題 6
仮説 3 を確かめよ.
□ レポート課題 7
R2 を自分の考えで求めてみよ(グラフでもよし,計算でもよし).
→ ただし,グラフで求めるには上で作った関数などでは「目が粗すぎる」ので,
少し細かくして使うとよい.
そのかわり、計算時間はかかるが…
さて,肝心の,われわれが感じた「でたらめさ」とはどういうものか,についてはまだまだ考察が足りない.
それについてはまた次回としよう.
>> 目次
 Out[7]= {0.2, 0.64, 0.9216, 0.289014, 0.821939, 0.585421, 0.970813, 0.113339,
0.401974, 0.961563, 0.147837, 0.503924, 0.999938, 0.000246305, 0.000984976,
0.00393603, 0.0156821, 0.0617448, 0.23173, 0.712124, 0.820014, 0.590364,
0.967337, 0.126384, 0.441645, 0.986379, 0.053742, 0.203415, 0.64815,
0.912207, 0.320342, 0.870893, 0.449755, 0.989902, 0.0399856, 0.153547,
0.519882, 0.998419, 0.00631451, 0.0250985, 0.0978744, 0.35318, 0.913776,
0.315159, 0.863335, 0.47195, 0.996853, 0.0125495, 0.0495681, 0.188445,
0.611733, 0.950063, 0.189772, 0.615035, 0.947067, 0.200523, 0.641254,
0.920189, 0.293764, 0.829868, 0.56475, 0.98323, 0.0659554, 0.246421,
0.742791, 0.76421, 0.720773, 0.805037, 0.62781, 0.934659, 0.244287}
← 数値としての結果も出力されるので安心(^-^).
Out[7]= {0.2, 0.64, 0.9216, 0.289014, 0.821939, 0.585421, 0.970813, 0.113339,
0.401974, 0.961563, 0.147837, 0.503924, 0.999938, 0.000246305, 0.000984976,
0.00393603, 0.0156821, 0.0617448, 0.23173, 0.712124, 0.820014, 0.590364,
0.967337, 0.126384, 0.441645, 0.986379, 0.053742, 0.203415, 0.64815,
0.912207, 0.320342, 0.870893, 0.449755, 0.989902, 0.0399856, 0.153547,
0.519882, 0.998419, 0.00631451, 0.0250985, 0.0978744, 0.35318, 0.913776,
0.315159, 0.863335, 0.47195, 0.996853, 0.0125495, 0.0495681, 0.188445,
0.611733, 0.950063, 0.189772, 0.615035, 0.947067, 0.200523, 0.641254,
0.920189, 0.293764, 0.829868, 0.56475, 0.98323, 0.0659554, 0.246421,
0.742791, 0.76421, 0.720773, 0.805037, 0.62781, 0.934659, 0.244287}
← 数値としての結果も出力されるので安心(^-^).
 ← R = 1.0: v = ゼロに収束していく?
In[9]:= LogisticPlot[0.2, 1.5, 70];
← R = 1.0: v = ゼロに収束していく?
In[9]:= LogisticPlot[0.2, 1.5, 70];
 ← R = 1.5: v = 0.3... 辺りに収束か.
In[10]:= LogisticPlot[0.2, 2, 70];
← R = 1.5: v = 0.3... 辺りに収束か.
In[10]:= LogisticPlot[0.2, 2, 70];
 ← R = 2.0: v = 0.5 に収束か.
In[11]:= LogisticPlot[0.2, 2.5, 70];
← R = 2.0: v = 0.5 に収束か.
In[11]:= LogisticPlot[0.2, 2.5, 70];
 ← R = 2.5: v = 0.6 に収束か.
In[12]:= LogisticPlot[0.2, 3, 70];
← R = 2.5: v = 0.6 に収束か.
In[12]:= LogisticPlot[0.2, 3, 70];
 ← R = 3.0: 2つの値の間を振動? ← 判断にはもっと多くの点が必要
In[13]:= LogisticPlot[0.2, 3.5, 70];
← R = 3.0: 2つの値の間を振動? ← 判断にはもっと多くの点が必要
In[13]:= LogisticPlot[0.2, 3.5, 70];
 ← R = 3.5: 4つの値の間を振動?
In[14]:= LogisticPlot[0.2, 4, 70];
← R = 3.5: 4つの値の間を振動?
In[14]:= LogisticPlot[0.2, 4, 70];
 ← お? R1 は 3 付近ということか?
In[23]:= LogisticLimitGraph[0.2, 2.95, 3.05]; ← R = 2.95 〜 3.05 周囲を拡大して計算…
← お? R1 は 3 付近ということか?
In[23]:= LogisticLimitGraph[0.2, 2.95, 3.05]; ← R = 2.95 〜 3.05 周囲を拡大して計算…
 ← R1 はいくつぐらいだ?
← R1 はいくつぐらいだ?
