Julia の計算をもっと速く?
もちろんコードによるんだけど、数値計算の世界ではプログラムの計算時間の大半(90% を越えることも…)が線形計算にとられることは珍しくない. だから、Julia でプログラムするとき、線形計算が速いかどうかは結構大事な話.
Julia が内部でどんな解法を使っているか
というわけで、まずは少しずつ、Julia の線形計算について調べようと思うんだな.
手始めに、特に指定しないで普通に線形計算を julia にさせたとき、どんなアルゴリズム/ライブラリが使われるか、を見てみたい. 基本的に Julia は線形計算については BLAS と LAPACK を使うことになっているそうなので、そのあたりとのからみを見る方法がわかれば十分、かな.
そして、こういうときはマクロ @code_lowered を使うと,実際にどういうルーチンが呼ばれるかわかりやすい. 例えば、
N = 10
A = randn(N,N)
b = randn(N)
@code_lowered A \ b
なんてやると,次のような出力が出る.
1-element Array{Any,1}:
:($(Expr(:lambda, Any[:A,:B], Any[Any[Any[:A,:Any,0],Any[:B,:Any,0],Any[:m,:Any,18],Any[:n,:Any,18],Any[symbol("#s347"),:Any,2]],Any[],3,Any[]], :(begin # linalg/generic.jl, line 329:
GenSym(0) = (Base.LinAlg.size)(A)
#s347 = (top(start))(GenSym(0))
GenSym(1) = (top(indexed_next))(GenSym(0),1,#s347)
m = (top(getfield))(GenSym(1),1)
#s347 = (top(getfield))(GenSym(1),2)
GenSym(2) = (top(indexed_next))(GenSym(0),2,#s347)
n = (top(getfield))(GenSym(2),1)
#s347 = (top(getfield))(GenSym(2),2) # linalg/generic.jl, line 330:
unless m == n goto 3 # linalg/generic.jl, line 331:
unless (Base.LinAlg.istril)(A) goto 1 # linalg/generic.jl, line 332:
unless (Base.LinAlg.istriu)(A) goto 0 # linalg/generic.jl, line 333:
return (Base.LinAlg.Diagonal)(A) \ B
goto 1
0: # linalg/generic.jl, line 335:
return (Base.LinAlg.LowerTriangular)(A) \ B
1: # linalg/generic.jl, line 338:
unless (Base.LinAlg.istriu)(A) goto 2 # linalg/generic.jl, line 339:
return (Base.LinAlg.UpperTriangular)(A) \ B
2: # linalg/generic.jl, line 341:
return (Base.LinAlg.lufact)(A) \ B
3: # linalg/generic.jl, line 343:
return (Base.LinAlg.qrfact)(A,(top(apply_type))(Base.LinAlg.Val,true)) \ B
end))))
これを見ると、julia では、いろいろ場合分けをした挙句、一般の場合は、連立一次方程式を Base.LinAlg.lufact で、つまり、LU 分解によって計算しているらしいことがわかる. より詳しく知りたければ、
?lufact
と打ち込めば、
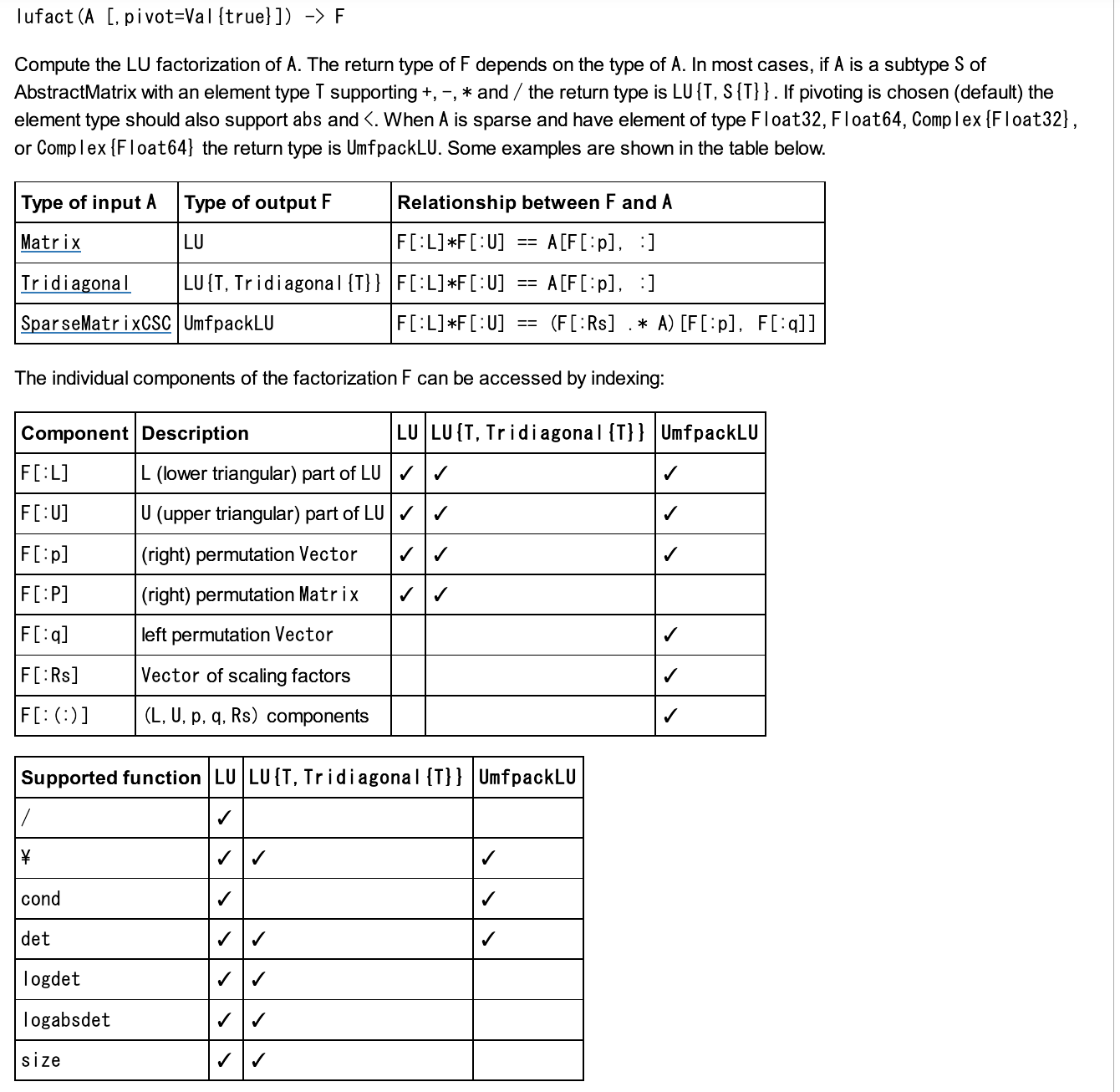
という感じで解説が出てくる(jupyter を使っている場合). そしてさらに、
methods(lufact)
とすると、multi dispatch による多重定義の source へのリンクをすべて出してくれるので,おおよそのところがわかる. この場合、たどってみると、さらに場合分けがあって、Julia 自前の LU分解関数 generic_lufact! が呼び出されるか、もしくは LAPACK の getrf が呼び出されるようで、まあいずれにせよ、LU 分解に基づくことになる. 結局、デフォルトでは、連立一次方程式の解を求めるための計算速度は LAPACK と BLAS によってほぼ決定されることになる.
同様に、 固有値問題, 例えば eigvals についても調べてみると、これについてはあまり凝ったことはしていなくて、ほぼ直接 LAPACK の geevx! を呼び出しているだけだ.
LAPACK を直接呼び出せる?
さらに蛇足を書いておくと、LAPACK の多くの命令を Julia から直接呼び出せる 1 .
例えば、julia の連立一次方程式解法よりも LAPACK の gesvx! の方が,条件数やエラー評価なんかを返してくれるので情報が多い. 同じ LU 分解なので計算結果は本質的に同じだが、gesvx! の方が計算しているものが多い分,ちょっとだけ遅いようだけど.
具体的には、julia から
LAPACK.gesvx!(A,b)
とすれば直接 LAPACK の gesvx! を使える.簡単だなあ、おい.
返ってくる数字の見方は,
?LAPACK.gesvx!
とすればマニュアルが出るので,その後半部分を読めばいい.まあ,あんまり使うことはなさそうだが.
近代的な解法は?
現状では、少なくとも CG 法系統の近代的な解法は Julia にデフォルトでは用意されていない. パッケージは複数あって、例えば KrylovMethods パッケージ に bicgstb 関数や cgls 関数などがあるし、 IDRsSolver パッケージ には IDR ソルバー idrs が用意されている.
ちょっとだけ bicgstb を試してみよう. 入力行列は疎行列型でないとダメなので,元行列が密行列型ならば
using KrylovMethods
N = 10
A = randn(N,N)
b = randn(N)
bicgstb(sparse(A),b)
などいう感じで入力することになる.
うん、ごく普通の小さな密行列を変換して入れると,よく知られたとおり「前処理をしない場合の」bicgstb はあまりよくない. 収束しないこともよくあるなあ. 前処理なしの乱暴な計算の場合は、同じパッケージ内の cgls の方がずっと安定しそうだ 2 . 実際ためしてみると、
using KrylovMethods
N = 10
A = randn(N,N)
b = randn(N)
x = cgls(sparse(A),b)[1]
A * x - b
として、誤差を出力させてみると、
10-element Array{Float64,1}:
-1.72892e-9
-1.31056e-8
3.0163e-9
7.52434e-9
7.79114e-9
2.21865e-9
-4.52298e-9
-3.2723e-9
-6.0486e-9
1.06731e-8
という感じの結果が得られる.うん、悪くないね.
同様に IDRsSolver パッケージの idrs 関数を試してみよう.
using IDRsSolver
N = 10
A = randn(N,N)
b = randn(N)
x = idrs(sparse(A),b)[1]
A * x - b
などとして誤差を出力してみると、
10-element Array{Float64,1}:
-1.15118e-11
5.93725e-12
9.61897e-12
5.97555e-12
-3.91798e-12
-1.44605e-11
3.85769e-12
1.02041e-11
-5.36537e-12
1.62759e-12
という感じで、こちらも前処理無しでなかなか悪くなさそうだ.
例えばこの idrs 関数でサイズを変えて試してみると、 100x100 のサイズで既に LU分解よりずっと速いように見える. もちろん,フル行列状態で大きくしていくと(疎行列のアクセスの問題で)かえって遅くなるので,きちんと「本当に」疎な行列で試してみる必要がありそうだ. というわけで、いずれ、大規模で疎な行列に対してこれらを試してみることにしますか.