偏微分方程式: 多次元問題

空間次元が多次元の偏微分方程式

空間次元が 2以上の偏微分方程式を扱ってみよう．

対象例: 相分離問題モデル: Cahn-Hilliard 方程式

たとえば比重の異なる二種類の物質を混ぜて放置すると，(軽いほうが上側に移動することから)全体はその二種類の物質ほぼそれぞれからなる二つの相に分離するという「相分離」現象が起きる．
注: もちろん，相分離現象を引き起こすメカニズムは他にもある．

こうした相分離現象のモデル方程式の一つが Cahn-Hilliard 方程式(wikipedia)で，多次元問題の数値計算の対象としてはなかなか面白いものである．この方程式の仕組みはあまり難しくないので，授業時に白板で解説しよう．

なお，この方程式は時間発展方程式なのだが，普通の手法で数値計算をしようとすると時間方向の刻み幅である $\Delta t$ を大変小さく取らないと不安定になる(数値解が発散する)性質を強く持つことでも知られている．そのため，相分離現象のシミュレーションを，という意味で計算したいのであればなかなか大変なのだが，今回は計算する空間を小さめに取り，かつ，空間次元も 2次元に抑えることでその雰囲気を味わってみよう．

さてこの Cahn-Hilliard 方程式であるが，対象とする関数 $u(\boldsymbol{x},t)$ に対して次のような偏微分方程式となっている( $u$ の peak 値が $\pm 1$ として問題のない範囲でパラメータを簡潔にしている)． \[ \frac{\partial u}{\partial t} = \Delta \left( -u + u^3 + q \, \Delta u \right) \] ただし，$q < 0$ は相の表面に働く表面張力の強さを表すパラメータで，その絶対値が大きいほど強いことになる．また，境界条件は本来は $\boldsymbol{n}$ を境界での外向き単位法線ベクトルとして以下のようになる．

$\left\{\begin{array}{rcl} \nabla u \cdot \boldsymbol{n} & = & 0, \cr \nabla (\Delta u) \cdot \boldsymbol{n} & = & 0. \end{array}\right.$

今回は本格的なシミュレーションが目的ではないので，まあ，この境界条件の代わりに，周期的境界条件を使うことにしよう(領域が矩形領域ならば，これらの境界条件の離散近似は難しくないが)．

手軽な手法の一つ: 線の方法(method of line) + Runge-Kutta 法で

では，偏微分方程式の数値解法の手軽な手法の一つである，「線の方法(method of line) + Runge-Kutta」で今回はチャレンジしてみよう．ちなみに，上に書いたようにこうした安直な手法だと Cahn-Hilliard 方程式の数値計算では $\Delta t$ をちょいと小さく取る必要があるので，そこは覚悟しておこう．

まず，空間領域 $\Omega = [0, L] \times [0, L]$ に対し、その分割数を $N_x \times N_x$ とし、境界条件として周期的境界条件を離散化しよう．

よって、$\Delta x = \Delta y = L / N_x$ として $u(\boldsymbol{x},t)$ の離散化に相当する従属変数を $ u(t) = \{ u_{i,j}(t)\}_{i, j = 1}^N$ とし、境界条件は外側にはみ出す点を仮想的に考えたとして

\[ \left\{ \begin{array}{rcl} \displaystyle u_{0, j} & := & u_{N, j} {\rm \,\,\, for \,\,\,} \forall j ,\cr\cr \displaystyle u_{N+1, j} & := & u_{1, j} {\,\,\, 同上 } , \cr\cr \displaystyle u_{i, 0} & := & u_{i, N} {\rm \,\,\, for \,\,\,} \forall i, \cr\cr \displaystyle u_{i, N+1} & := & u_{i, 1} {\,\,\, 同上 } \end{array} \right. \]

と解釈することになる．

こうしておいて、空間微分(ラプラシアン) $\Delta$ をたとえば差分近似で置き換える．たとえば $u$ に対するもとのラプラシアンが \[ \Delta u = \left( \frac{\partial}{\partial x} \right)^2 u + \left( \frac{\partial}{\partial y} \right)^2 u \]

であることから，その二階中心差分は \[ (\Delta_d \, u)_{i,j} := \frac{ u_{i+1,j} - 2 u_{i,j} + u_{i-1,j} }{\Delta x^2} + \frac{ u_{i,j+1} - 2 u_{i,j} + u_{i,j+1} }{\Delta y^2} \]

などとなる．

そして，これらを使って，もとの Cahn-Hilliard 方程式を線の方法で近似して得られる常微分方程式は \[ \frac{d u_{i,j}(t) }{dt} = \Delta_d \left( - u + u^3 + q \, \Delta_d u \right)_{i,j} \,\,\,\, \mbox{ for } i = 1,2,\cdots, N, j = 1,2,\cdots, N \]

という $N \times N$ 元連立常微分方程式で近似できることになる．

あとは少しずつプログラムを作っていくだけだ．まずは、問題のパラメータを設定してしまおう．

1
2
3
4
5
6


q = -0.001
L = 1.0
Nx = 50
Δx = L/Nx
Nt = 1000000
Δt = 1/Nt

次に、ラプラシアンをどうにか構成しよう．まず、そのために使う係数行列を下記のように定義する．

1
2
3
4
5
6
7


using LinearAlgebra
using SparseArrays

v = ones(Nx-1)
D = -2 * I + diagm(1 => v, -1 => v)
D[1,Nx] = D[Nx,1] = 1.0
D = sparse(  D / (Δx^2) )

50×50 SparseMatrixCSC{Float64,Int64} with 150 stored entries: [1 , 1] = -5000.0 [2 , 1] = 2500.0 [50, 1] = 2500.0 [1 , 2] = 2500.0 [2 , 2] = -5000.0 [3 , 2] = 2500.0 ⋮… [49, 48] = 2500.0 [48, 49] = 2500.0 [49, 49] = -5000.0 [50, 49] = 2500.0 [1 , 50] = 2500.0 [49, 50] = 2500.0 [50, 50] = -5000.0

こうしておいて、近似データそのものである行列 $u$ に対して、上で定義した行列 $D$ を用いた $D * u$ は行列 $u$ の行添字に関する二階差分になっている．

同様に、$u * D$ は行列 $u$ の列添字に関する二階差分になっているので、結局、これらの和である $D * u + u * D$ は $u$ に離散ラプラシアン $\Delta_d$ を適用した結果になる．

tips: 線形代数が苦手な人は、for 文を使ってプログラムしても良いが，まあなるべく線形代数を使えるようにしよう．

よって、微分方程式の右辺の近似計算式は次のようになるだろう．

1
2
3


Lapl(u) =  D * u + u * D

f(u) = Lapl( - u + u.^3 + q * Lapl(u) )

f (generic function with 1 method)

さて、これで連立常微分方程式の右辺(の近似)が計算できたことになるので、いつものように Runge-Kutta 法を定義する．

1
2
3
4
5
6
7


function RK(u)
    f1 = f(u)
    f2 = f(u + Δt/2 * f1)
    f3 = f(u + Δt/2 * f2)
    f4 = f(u + Δt * f3)
    return u + Δt * (f1 + 2*f2 + 2*f3 + f4)/6
end

RK (generic function with 1 method)

これで計算手順の準備は整った．

次に、初期値を適当に作ろう．今回は「最初は二種類の物質をなるべく均等にかき混ぜた状態」を初期状態にするシチュエーションを考えて，$u \cong 0$ な状態を乱数で作り出そう．

1

u0 = 0.01 * (rand(Nx, Nx) .- 0.5)

50×50 Array{Float64,2}: 0.000907744 -0.0039247 -0.00189216 … -2.25458e-5 -0.000703019 0.000359209 0.00475919 -0.00200338 0.00139821 -0.00344962 … (値は乱数のため，やるたびに異なる)

どんな初期値なのか、目で見ておこう．

1
2
3
4
5
6


using Plots
default( fmt = :png, aspectratio = 1.0, ticks = nothing, framestyle = :none)
# fmt = :png として、図を、ファイル容量の小さい png 形式で描かせている．

X = Y = Δx:Δx:L
heatmap(X, Y, u0) 

png

さて、これで準備は整ったので、早速、計算してみよう. Juliabox が混んでいなければ、6～7分ほどで計算が終わるだろう(教員の PC だと 4分半ほどだ)．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15


using ProgressMeter

u = copy(u0)
sq_u = copy(u0)

n_last = round(Int, Nt)
n_skip = round(Int, n_last/200)

@showprogress for i in 1:n_last
    global u, sq_u
    u = RK(u)
    if i % n_skip == 0  # 一定数ステップおきにデータを格納するとして
        sq_u = cat(sq_u, u, dims = (3) )  # 3次元目に追加していく
    end
end

Progress: 100%|█████████████████████████████████████████| Time: 0:06:46

試しに結果の数字をちょろっと見てみる．

1

sq_u

50×50×201 Array{Float64,3}: [:, :, 1] = 0.000907744 -0.0039247 -0.00189216 … -2.25458e-5 -0.000703019 0.000359209 0.00475919 -0.00200338 0.00139821 -0.00344962 > … [:, :, 2] = -0.000811457 -0.00144386 -0.00211925 … 0.00024822 -0.000244266 -0.000153012 -0.000554191 -0.00112487 0.000227066 9.30991e-5 > … (値は乱数のため，やるたびに異なる)

あまり変なことにはなっていなさそうなので、最終結果をまずはプロットしてみよう．こういう場合は heatmap 関数を使うのが良さそうだ．

1

heatmap(X, Y, sq_u[:,:,end])

png

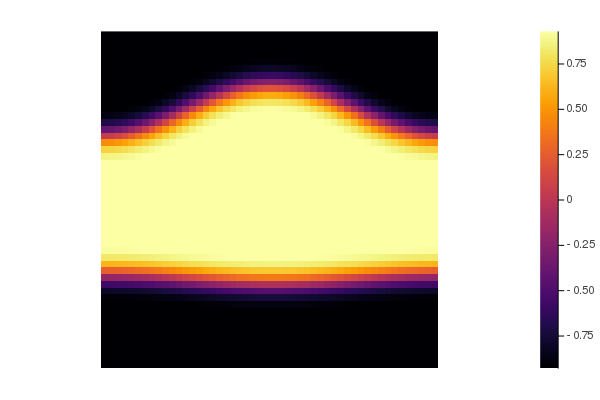
ふむ，確かに分離しているようだな(初期値が乱数なので，貴殿の結果がこの図と異なってもそれは「当然」だ)．

ちなみに，最終結果の $u$ の値のスケールで初期値をあらためてプロットして，「初期値がたしかに均等っぽい」ことも確認しておこう．それには，計算値全体の最大値と最小値をまず次のように調べて，

1

vrange = ( minimum(sq_u), maximum(sq_u) )

(-0.9296099751372866, 0.9296005507180825)

次のように clim オプションで値の上下を固定して heatmap を使えば良い．

1

heatmap(X, Y, u0, clim = vrange)

png

確かに，時間発展結果に比べると初期値は「ほぼ均等にゼロに近い」ことが見て取れる．よし．

ということで，ふむ、なんとなくうまく計算できているようだ．

すべてのデータを一気に画像化する

あとは heatmapコマンドを好きなだけ繰り返せば途中結果も見られる．しかしまあそれはそれで様子がよくわからないので全データを画像 & 動画にしてしまうことを考えよう．

まず、たくさんの画像ファイルを入れておくディレクトリをコマンドで作らせよう．これは一回だけやれば良い．

1

run(`mkdir figures`)

Process(mkdir figures, ProcessExited(0))

注: 上の “mkdir” の実行後、juliabox のファイルビューアー部分を見てみよう．figures という新しいディレクトリができているはずだ．

次に、データを画像ファイルとして保存するコマンドを作ろう．基本的には、plot 系コマンドの直後に savefig コマンドを使うだけで、そのグラフを画像ファイルとして保存できる．今回は動画ファイルの「元」にしたいので、そうだなあ、”4桁の数字.png” というファイル名になるようにしておく．

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


using Printf # すぐ下の @sprintf を使いたいので．

default( clim = vrange )
# 画像全て，同じ値スケールで色を塗る．

function figure(num)
    s = @sprintf("%8.7f", num * Δt)
    heatmap(X, Y, sq_u[:,:,num], title = "t = $s")
    # 時間も一緒に表示している．

    savefig( "figures/" * @sprintf("%04d", num) * ".png" )
    # 4桁の数字.png というファイル名で保存する
end

注: “@sprintf” というマクロは、昔から C 系統のプログラム言語で使われている sprintf 命令を模したもので、文字列を「決まったフォーマットで出力する」ものだ．使い方は “sprntf” などで検索してみよう．

では、全データからたくさんの画像ファイルを作ろう．これは 15秒程度で終わるだろう．

1
2
3


@showprogress for n in 1:size(sq_u)[3]
    figure(n)
end

Progress: 100%|█████████████████████████████████████████| Time: 0:00:16

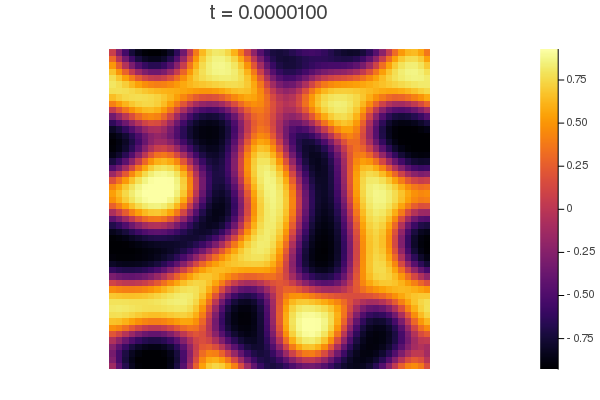
そして juliabox のファイルビューアー部分で．figures ディレクトリの下を見てみよう．今回は 201個の画像ファイルが生成されているはずだ．たとえばその 0010.png を見てみると次のような感じになっているだろう．
png

ffmpeg などの動画作成ツールで動画にしてみよう

さて，数百個もの画像ファイルが有るならばこれをつなげて動画にするのが可視化としては「いつもの手」というやつだ．そして世の中には有名なフリーのツールに ffmpeg というものがあり、これを使うと連番の画像ファイルを無理なくきれいに動画にできる．この手法は便利なので覚えておこう．

今の juliabox にはこれがインストールされていて使えるので見逃す手は無い．自分の PC で実習をしていて ffmpeg がインストールされていない、という人は、これを機にインストールしておこう．

さて、今回は ffmpeg を julia から直接呼び出して使ってみよう．以下のようにすればよいだろう．

(詳しい人向け: terminal からコマンドを打っても良い)

1

run(`ffmpeg -y -r 10 -i "figures/%04d.png" -pix_fmt yuv420p -s 1200x800 ch-eq.mp4`)

ffmpeg version 2.8.15-0ubuntu0.16.04.1 Copyright © 2000-2018 the FFmpeg developers built with gcc 5.4.0 (Ubuntu 5.4.0-6ubuntu1~16.04.10) 20160609 configuration: –prefix=/usr –extra-version=0ubuntu0.16.04.1 - …

これで ch-eq.mp4 という動画ファイルができたはずだ． julia/jyupiter のファイル操作画面で、その動画ファイルを view したり、ダウンロードして(jupyter はファイルを1つずつなら指定してから download できるぞ)動かしてみるなどして、確認しよう．

参考のために、そのファイルをここに直接おいておく．

得られる動画ファイル (mp4 形式)

Report No.12

上の例では初期値を乱数で作ったが，そうでない初期値を自分で作ってそれに対して計算してみよう．ただし，$-1 < u(\boldsymbol{x}, 0) < 1$ を満たすようにしておくことを忘れないように．
今回は空間方向だけ差分化して、あとは常微分方程式として扱うという「線の方法」をとった．時間方向も差分化したり、有限要素法を使ったり(かなり面倒だが)他の方法で計算してみよう．できれば「高速な計算」を試みると良いだろう．