¼ø¶È»ñÎÁ/02

ÈóÀþ·ÁÊýÄø¼° f(x)=0 ¤Îµá²ò †

↑

Æóʬˡ(ÄêµÁ°è¤¬1¼¡¸µ¤Î»þ) †

²ò¤¬´Þ¤Þ¤ì¤Æ¤¤¤ë¤Ï¤º¤ÎÈϰϤòȾʬ¤Ë¾®¤µ¤¯¤·¤Æ¤¤¤¯È¿ÉüË¡¡¥ ´Ø¿ô¤¬Ï¢Â³¤Ç¡¢²ò¤¬´Þ¤Þ¤ì¤Æ¤¤¤ë¤Ï¤º¤ÎÈÏ°Ï(Â礭¤¯¤Æ¤âÎɤ¤)¤ò°ì¤ÄÃΤäƤ¤¤ì¤Ð OK.

↑

¥µ¥ó¥×¥ë¥×¥í¥°¥é¥à †

  1. include Math

  2.  

  3. def f(x)

  4.   return sin(x)

  5. end

  6.  

  7. em = 1.0*2**(-53)

  8. criteria = 1.2*em # Because sin(x) is almost -(x-PI) around PI.

  9.  

  10. x_l = 0.7*PI

  11. x_r = 1.5*PI

  12.  

  13. while (x_r - x_l > (2*em)*x_l) do

  14.   x_m = (x_r + x_l)/2.0

  15.   if (f(x_m).abs > criteria) then

  16.     if (f(x_l)*f(x_m) < 0) then

  17.       x_r = x_m

  18.     else

  19.       x_l = x_m

  20.     end

  21.   else

  22.     break

  23.   end

  24. end

  25.  

  26. print("Finished. x: ",x_m,", f(x): ",f(x_m),"\n")
↑

ÉÔÆ°ÅÀÌäÂê¤Ë½ñ¤­´¹¤¨¤Æ¡¢ÉÔÆ°ÅÀ¤òµá¤á¤ëÊýË¡¡¥ †

f(x) = 0 ¤ò²ò¤¯Âå¤ï¤ê¤Ë¡¢g(x) := f(x) + x = x ¤È¤¤¤¦ÉÔÆ°ÅÀÌäÂê¤ÎÉÔÆ°ÅÀ¤òÀ⤯ÌäÂê¤ËÃÖ¤­´¹¤¨¤ë¡¥ ¤³¤ÎºÝ¡¢g(x) ¤¬½Ì¾®¼ÌÁü¤Ê¤é¤Ð x_new := g(x_old) ¤È¤¤¤¦È¿Éü¤ÇÉÔÆ°ÅÀ¤Ø¶á¤Å¤¯¡¥

↑

¥µ¥ó¥×¥ë¥×¥í¥°¥é¥à †

  1. include Math

  2.  

  3. def f(x)

  4.   return exp(-x)-x

  5. end

  6.  

  7. def g(x)

  8.   exp(-x)

  9. end

  10.  

  11. # criterion

  12. cri_f = 1.0e-15

  13.  

  14. # initial data

  15. x = 0.5

  16.  

  17. # iteration number 

  18. n = 0

  19.  

  20. while (f(x).abs > cri_f) do

  21.   x = g(x)

  22.   n += 1

  23.   print(n, " ",f(x).abs, "\n")

  24. end
↑

Newton Ë¡ †

(ÀâÌÀά)

↑

¥µ¥ó¥×¥ë¥×¥í¥°¥é¥à †

  1. include Math

  2.  

  3. Sqt = sqrt(3.0)

  4.  

  5. def f(x,y)

  6.   f_x = x**2+y**2 -1.0

  7.   f_y = Sqt*x-y

  8.   return [f_x,f_y]

  9. end

  10.  

  11. def one_newton(x,y)

  12.   denom = 2.0*(x+Sqt*y)

  13.   u,v = f(x,y)

  14.   new_x = x - ((u+2*y*v)/denom)

  15.   new_y = y - ((Sqt*u-2*x*v)/denom)

  16.   return [new_x,new_y]

  17. end

  18.  

  19. limit_loop = 100

  20. Em = 1.0*2**(-53)

  21. tol_err = 10.0*Em

  22.  

  23. x,y = 0.5,0.5

  24.  

  25. for i in 0..limit_loop do

  26.   f_x,f_y = f(x,y)

  27.   print(i,", ",x,", ",y,", ",f_x,", ",f_y,"\n")

  28.   if ((f_x.abs < tol_err) && (f_y.abs < tol_err)) then

  29.     break

  30.   end

  31.   x,y = one_newton(x,y)

  32. end

  33.  

  34. # output example.

  35.  

  36. 0, 0.5, 0.5, -0.5, 0.366025403784439

  37. 1, 0.549038105676658, 0.950961894323342, 0.205771365940052, 0.0

  38. 2, 0.502189953469069, 0.869818514459077, 0.0087789974610617, 1.11022302462516e-16

  39. 3, 0.500004774982219, 0.866033674296247, 1.91000200775449e-05, 0.0

  40. 4, 0.5000000000228, 0.86602540382393, 9.12012687592778e-11, 0.0

  41. 5, 0.5, 0.866025403784439, -1.11022302462516e-16, 0.0
↑

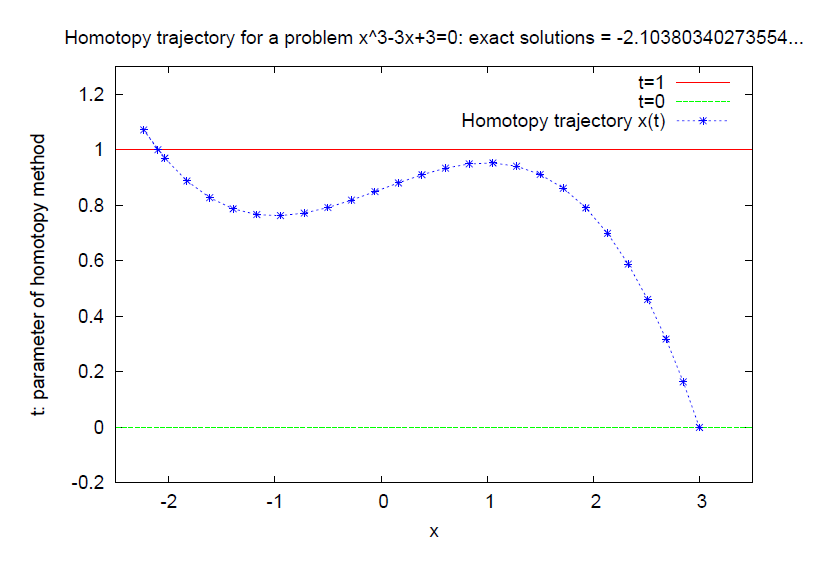
¥Û¥â¥È¥Ô¡¼Ë¡ †

(ÀâÌÀά)

↑

¤Þ¤¸¤á¤Ê¼ÂÁõ¥µ¥ó¥×¥ë †

  1. # Homotopy method to obtain a solution f(x) = x^3-3x+3 = 0.

  2. include Math

  3.  

  4. # error, parameters and initial value

  5. Em = 1.0*2**(-53)

  6. Tol_err = Em*(10.0**2)

  7.  

  8. # We change the homotopy method to the normal Newton method 

  9. # when |t-1| < DS or t > 1.

  10. DS = 0.01

  11.  

  12. # Initial value

  13. Ini_x = 3.0

  14.  

  15. # Approximate distance of one movement on the trajectory.

  16. Dl = 0.05

  17.  

  18. # The target function f and its derivative.

  19. def f(x)

  20.   return x**3 -3.0*x +3.0

  21. end

  22.  

  23. def df(x)

  24.   return 3.0*(x**2) -3.0

  25. end

  26.  

  27. # One iteration of Newton method about the function f.

  28. def newton_one_iteration_f(x)

  29.   return x - f(x)/df(x)

  30. end

  31.  

  32. # Newton method to obtain a numerical solution of f(x)=0.

  33. def newton_f(x)

  34.   y = x

  35.   while f(y).abs >Tol_err do

  36.     y = newton_one_iteration_f(y)

  37.   end

  38.   return y

  39. end

  40.  

  41. # Initial value of the function f.

  42. Fw = f(Ini_x)

  43.  

  44. # Approximate movement direction.

  45. def d(x,t)

  46.   gamma = - df(x)/Fw

  47.   dx = - sqrt(Dl/(1.0+(gamma**2)))

  48.   dt = gamma * dx

  49.   return [dx,dt]

  50. end

  51.  

  52. # The function q to be zero on fine movements and its derivative.

  53. def q(dt_tilde,x,t,dx,dt)

  54.   zeta = - dt/dx

  55.   return f(x+dx+zeta*dt_tilde)+(t+dt+dt_tilde - 1.0)*Fw

  56. end

  57.  

  58. def dq(dt_tilde,x,t,dx,dt)

  59.   zeta = - dt/dx

  60.   return df(x+dx+zeta*dt_tilde)*zeta + Fw

  61. end

  62.  

  63. # One iteration of Newton method about the function q.

  64. def newton_one_iteration_q(dt_tilde,x,t,dx,dt)

  65.   return dt_tilde - q(dt_tilde,x,t,dx,dt)/dq(dt_tilde,x,t,dx,dt)

  66. end

  67.  

  68. # Newton method to obtain a numerical solution of q(...)=0.

  69. def newton_q(dt_tilde,x,t,dx,dt)

  70.   y = dt_tilde

  71.   while q(y,x,t,dx,dt).abs >Tol_err do

  72.     y = newton_one_iteration_q(y,x,t,dx,dt)

  73.   end

  74.   return y

  75. end

  76.  

  77. ###################################

  78. # Via a fixed homotopy method we compute numerical solutions

  79. # "x" from t = 0 to t = 1. The last obtained "x" is a numerical

  80. # solution of f(x)=0.

  81.  

  82. t = 0.0

  83. x = Ini_x

  84. print(t," ",x,"\n")

  85.  

  86. while (1.0-t) > DS do

  87.   dx,dt = d(x,t)

  88.   zeta = - dt/dx

  89.   dt_tilde = newton_q(0.0, x,t,dx,dt)

  90.   dx_tilde = zeta*dt_tilde

  91.   x += dx + dx_tilde

  92.   t += dt + dt_tilde

  93.   print(t," ",x,"\n")

  94. end

  95.  

  96. # We use normal Newton method when (1.0-t) <= DS.

  97. x = newton_f(x)

  98. print "1.00000000000000 ",x,"\n"
↑

¾å¤Î·ë²Ì †

homotopy2-dat.png

źÉÕ¥Õ¥¡¥¤¥ë: filehomotopy2-dat.png 891·ï [¾ÜºÙ]