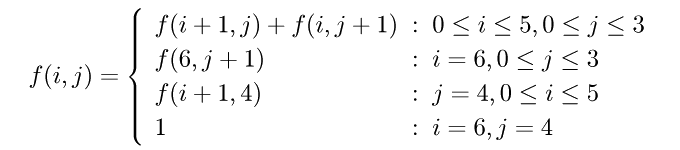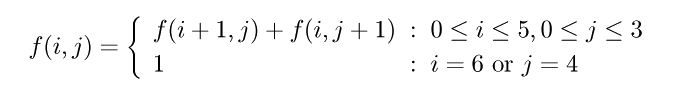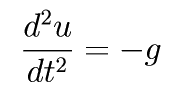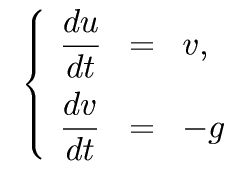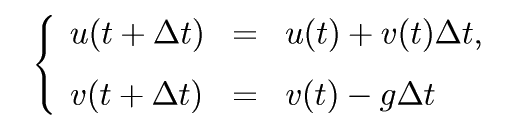¼ø¶È»ñÎÁ/13
Á°²ó¤Î²ÝÂê¤Ë¤Ä¤¤¤Æ †
Á°²ó¤ÎÁí»Å¾å¤²¤Ï¡¤Í¿¤¨¤é¤ì¤¿ÃÏ¿Þ¤ÎÆóÅÀ´Ö¤ÇºÇû·ÐÏ©¤òÆ»¤¬²¿Ä̤ꤢ¤ë¤«¿ô¤¨¤è¤È¤¤¤¦¤â¤Î¤Ç¤¢¤Ã¤¿¡¥
(ÃϿޤˤĤ¤¤Æ¤ÏÁ°²ó¤Î web ¤ò»²¾È¤Î¤³¤È)
¿Þ¤¬Èó¾ï¤ËÁÇľ¤Ç´Êñ¤Ê·Á¤ò¤·¤Æ¤¤¤ë¤Î¤Ç¡¤ºÇû·ÐÏ©¤Î¸Ä¿ô¤ò¿ô¤¨¤ë¤Ë¤Ïñ½ã¤Ê¥ë¡¼¥ë¤Ç¤Ç¤¤ë¤³¤È¤ÏÁ°²ó¤Î¥Ò¥ó¥È¤«¤é¤ï¤«¤Ã¤¿¤È»×¤¦¡¥
¶ñÂÎŪ¤Ë¤Ï¡¤
¡Ö¤¢¤ëÅÀ¤òÄ̤ëºÇû·ÐÏ©¤Ï¡¤¤½¤Î¾å¤ÎÅÀ¤«±¦¤ÎÅÀ¤òÄ̤äƤä¤Ã¤Æ¤¯¤ë¡×
¤Î¤Ç¡¤¤³¤ì¤Ï¸À¤¤´¹¤¨¤ë¤È¡¤
¡Ö¤¢¤ëÅÀ¤òÄ̤ëºÇû·ÐÏ©¤Î¿ô = ¤½¤Î¾å¤ÎÅÀ¤òÄ̤ëºÇû·ÐÏ©¤Î¿ô + ¤½¤Î±¦¤ÎÅÀ¤òÄ̤ëºÇû·ÐÏ©¤Î¿ô¡×
¤È¤¤¤¦¤³¤È¤Ë¤Ê¤ë¡¥¤¢¤È¤Ï¤³¤ì¤ò¶ñÂÎŪ¤Ë¤·¤Æ¤¤¤±¤Ð¤è¤¤¡¥
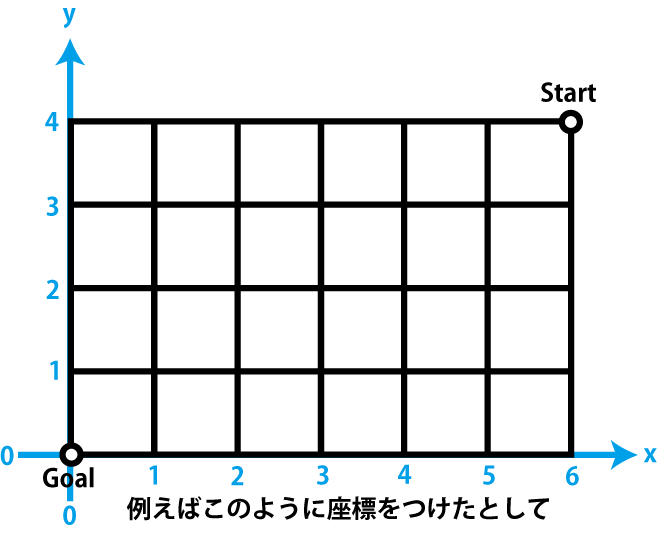
Î㤨¤ÐÃÏ¿Þ¤òÁÇľ¤Ë x,y ºÂɸ¤Ç°Ê²¼¤Î¤è¤¦¤ËÆÃħÉÕ¤±¤¿¤È¤·¤Æ¡¤
¤Î¤è¤¦¤Ë¹Í¤¨¤¿¤È¤·¤è¤¦¡¥
¤³¤Î¤È¤¡¤ºÂɸ (i,j) (0 ≤ i ≤ 6, 0 ≤ j ≤ 4)¤ÎÅÀ¤òÄ̤ëºÇû·ÐÏ©¤Î¿ô¤ò f(i,j)¤È¤¹¤ë¤È¡¤¿ô¼°¤Ëľ¤»¤Ð°Ê²¼¤Î¤è¤¦¤Ê´Ø·¸¼°¤¬À®¤êΩ¤Ä¤³¤È¤¬Ê¬¤«¤ë¡¥
¤È¤Ê¤ë¤Î¤Ç¡¤¤³¤ì¤ò»È¤¨¤Ð¤è¤¤¡¥¤¢¤È¤Ï¡¤¤³¤Î´Ø·¸¼°¤òÅú¤¨¤Ë¶á¤¤Êý¤«¤é»È¤¦¤«±ó¤¤Êý¤«¤é»È¤¦¤«¤Ç¥×¥í¥°¥é¥à¤Î½ñ¤Êý¤¬°ã¤¦¤À¤±¤À¡¥
¤Ê¤ª¡¤¾å¤Î¼°¤òÅÓÃæ¤Þ¤Ç¼ê¤ÇŸ³«¤·¤¿·Á¤Î
¤ò»È¤Ã¤Æ¤âÎɤ¤¡¥¤¿¤À¡¤¤³¤¦¤¤¤¦¤è¤¦¤Ë¡Ö¿Í´Ö¤¬ÅÓÃæ¤Þ¤Ç²ðÆþ¤¹¤ë»þ¤Ë·×»»¤ò¼ºÇÔ¤¹¤ë¤³¤È¤¬¤¢¤ë¡×¤Î¤Ç¡¤°ìÈÌŪ¤Ë¤Ï¤É¤³¤Þ¤Ç²ðÆþ¤¹¤ë¤«¤ÏǺ¤Þ¤·¤¤ÌäÂê¤À¡¥¤³¤ÎÌäÂê¤Î¾ì¹ç¤Ï¤Þ¤º´Ö°ã¤¨¤Ê¤¤¤À¤í¤¦¤¬¡Ä
ºÆµ¢ÄêµÁ¤ò»È¤¦¾ì¹ç †
¤³¤ì¤Ï¿ô¼°¤òÁÇľ¤Ë»È¤¨¤Ð¤è¤¤¤Î¤Ç¡¤Î㤨¤Ð°Ê²¼¤Î¤è¤¦¤Ë¤Ê¤ë¤À¤í¤¦¡¥
ưŪ·×²èË¡¤â¤É¤¤ò»È¤¦¾ì¹ç †
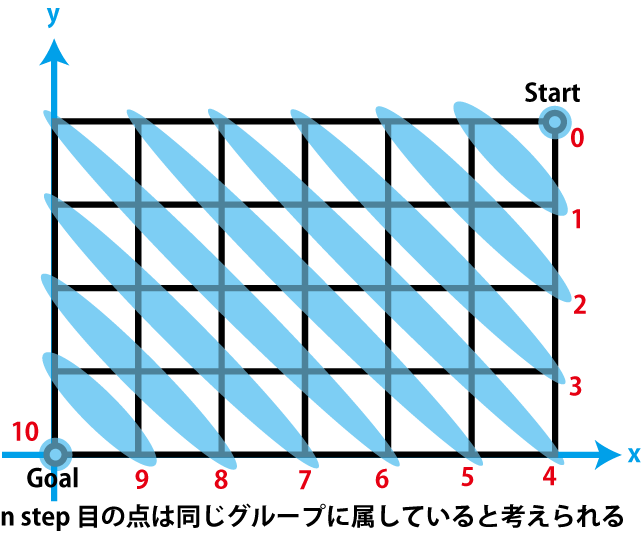
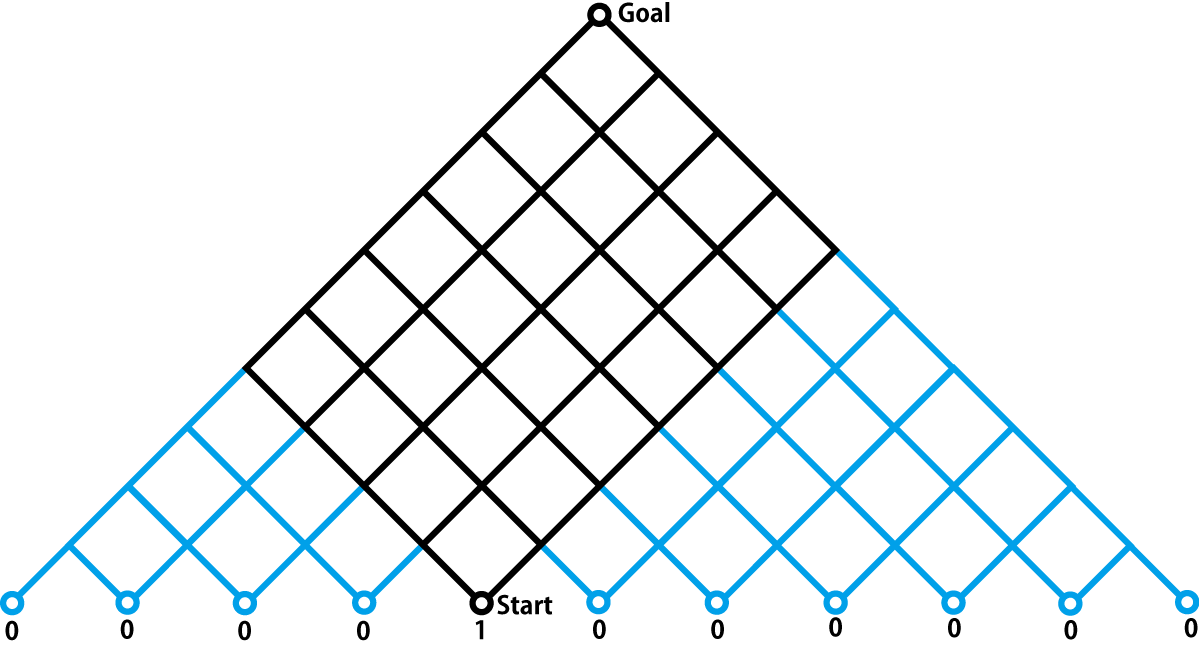
±¦¾å¤Î Start ÃÏÅÀ¤«¤é¡¤¡Ö²¿¥¹¥Æ¥Ã¥×Ìܤ«¡×¤È¤¤¤¦¤³¤È¤ËÃåÌܤ¹¤ì¤Ð¡¤¥¹¥Æ¥Ã¥×¿ô¤òÁý¤ä¤·¤Æ¤¤¤¯¤è¤¦¤Ë·×»»¤ò¿Ê¤á¤ì¤Ð¤è¤¤¤³¤È¤Ëµ¤¤Å¤¯¡¥¤Ä¤Þ¤ê¡¤¼¡¤Î¿Þ¤ÎÀÖ¤¤Ê¸»ú¤Î½ç¤Ë·×»»¤¬¿Ê¤á¤é¤ì¤ë¤Ù¤¤À¤È¤¤¤¦¤³¤È¤¬¤ï¤«¤ë¤À¤í¤¦¡¥
¾¯¤·¹©Éפ¬¤¤¤ë¤¬¡¤¤Þ¤¢Î㤨¤Ð¼¡¤Î¤è¤¦¤Ë¥×¥í¥°¥é¥à¤ò½ñ¤±¤ë¤À¤í¤¦¡¥
¾¯¤·¸¤¤¹Í¤¨Êý †
ºÇû·ÐÏ©¿ô¤Î°Í¸´Ø·¸¤ò¹Í¤¨¤ë¤È¡Ö±¦¾å¤«¤éº¸²¼¤Ë¼Ð¤á¡×¤ËÏ䬿ʤळ¤È¤¬¤ï¤«¤ë¡¥
¸À¤¤´¹¤¨¤ë¤È¡¤¡Ö¤³¤Î¼Ð¤á¤ÎÊý¸þ¤¬ÁÇľ¤ÊÊý¸þ¡×¤Ë¤Ê¤ë¤Î¤Ç¡¤¤³¤ÎÊý¸þ¤Ë¿Þ¤ò·¹¤±¤Æ¹Í¤¨¤ë¤Î¤¬ÏÀÍýŪ¤ËÁÇľ¤À¤È¤¤¤¦¤³¤È¤Ë¤Ê¤ë¡¥
¼ÂºÝ¤Ë·¹¤±¤Æ¤ß¤è¤¦¡¥
¤¹¤ë¤È¡¤°Í¸´Ø·¸¤¬Á°²ó¤Î¡ÖÌÚ¹½Â¤¡×¤Î¤È¤³¤í¤Ç¤ä¤Ã¤¿ÏäÈÁ´¤¯Æ±¤¸¤Ê¤Î¤Ç¡¤¤¸¤Ä¤ÏƱÍͤˡÖÌÚ¹½Â¤¡×¤Ç¹Í¤¨¤ë¤È¤è¤êʬ¤«¤ê¤ä¤¹¤¤¤È¤¤¤¦¤³¤È¤â¿ä¬¤¬¤Ä¤¯¡¥
¤½¤³¤Ç¡¤¤¿¤È¤¨¤ÐÁ´ÂΤ¬¡Ö¤ï¤«¤ê¤ä¤¹¤¤ÌÚ¹½Â¤¡×¤Ë¤Ê¤ë¤è¤¦¤Ë¤µ¤é¤ËÃÏ¿Þ¤ò¾¯¤·ÉÁ¤Â¤·¡¤Á´ÂΤΤĤ¸¤Ä¤Þ¤¬¹ç¤¦¤è¤¦¤Ë¡ÖÍաפ˿ô»ú¤ò¤Ä¤±¤ë¤È°Ê²¼¤Î¤è¤¦¤Ê¿Þ¤Ë¤Ê¤ë¡¥
¤¢¤È¤Ï¡¤²¼¤Î¿ô»ú¤ò¤¹¤È¼«Ê¬¤Î¿ô»ú¤Ë¤Ê¤ë¡¤¤È¤¤¤¦»ÅÁȤߤòÁ°²ó¤ÈƱ¤¸¤è¤¦¤Ë¥×¥í¥°¥é¥à¤¹¤ë¤À¤±¤À¡¥
¤³¤ì¤Ç¹Í¤¨¤ë¤È¡¤Æ°Åª·×²èË¡¤â¤É¤¤Î¥×¥í¥°¥é¥ß¥ó¥°¤â¾å¤È°ã¤Ã¤Æ¿ïʬ´Êñ¤Ë½ñ¤±¤ë¤Ï¤º¤À¡¥
·×»»Î̤ÏÁý¤¨¤ë¤¬¡¤¤³¤¦¤·¤¿ÁÇľ¤Ê¥×¥í¥°¥é¥à¤Ë¤Ï¥ß¥¹¤¬Æþ¤ë³ÎΨ¤ÏÃʰ㤤¤ËÄ㤯¤Ê¤ë¡¥
Åú¤¨¤¬´Ö°ã¤Ã¤Æ¤¤¤ì¤Ð°ÕÌ£¤¬Ìµ¤¤¤Î¤À¤«¤é¡¤¤Þ¤º¤Ï¤³¤¦¤·¤¿¡ÖÁÇľ¤Ê¡×¡Ö³Î¼Â¤Ê¡×¥×¥í¥°¥é¥à¤òÌܻؤ½¤¦¡¥
¤³¤Î¤è¤¦¤Ë¡¤
Áí¹çÎÏ: ÈùʬÊýÄø¼°¤ò²ò¤¤¤Æ, ²ò¤ò¸«¤Æ¤ß¤è¤¦ †
¤³¤ì¤Þ¤Ç¤Ç¥×¥í¥°¥é¥ß¥ó¥°¤Ë¤Ä¤¤¤ÆºÇÄã¸Â¤ÎÃμ±¤Ï¿È¤Ë¤Ä¤±¤¿¤Î¤Ç¡¤¾¯¤·±þÍѤظþ¤±¤Æ¼Â½¬¤ò¹Ô¤Ã¤Æ¤ß¤è¤¦¡¥
¤¤¤í¤ó¤ÊÂêºà¤¬¤¢¤ë¤¬¡¤¤Þ¤º¤Ï¤´¤¯´Êñ¤Ê¾ïÈùʬÊýÄø¼°¤ËÂФ·¤Æ¡¤¶á»÷·×»»¤ò¤·¤Æ¶á»÷²ò¤òµá¤á¤Æ¤½¤ÎÍͻҤò¤ß¤ë¤È¤¤¤¦°ìÏ¢¤Îή¤ì¤ò¤ä¤Ã¤Æ¤ß¤è¤¦¡¥
¼«Í³Íî²¼¤ò¥·¥ß¥å¥ì¡¼¥È¤·¤Æ¤ß¤ë †
³ØÀ¸¤¬ºÇ¤â¤è¤¯ÃΤäƤ¤¤ë¾ïÈùʬÊýÄø¼°¤Ç¤¢¤ë¡¤Newton Îϳؤ˴ð¤Å¤¯±¿Æ°ÊýÄø¼°¤òÂêºà¤Ë¼è¤ê¾å¤²¤è¤¦¡¥
¤Þ¤º¤â¤Ã¤È¤â´Êñ¤Ê¡¤¡Ö¿¿¶õÃæ¤òʪÂΤ¬¼«Í³Íî²¼¤·¤Æ¤¯¤ëÍͻҡפò¹Í¤¨¤è¤¦¡¥
»þ´Ö¤ò t sec, ÃϾ夫¤é¤ÎʪÂΤι⤵¤ò u(t) m¡¤½ÅÎϲîÅÙ g = 9.8 m/(s^2) ¤È¤¹¤ë¤È¡¤
Newton ¤Î±¿Æ°ÊýÄø¼° F = ma ¤è¤ê¡¤
¤È¤¤¤¦¾ïÈùʬÊýÄø¼°¤¬ÆÀ¤é¤ì¤ë¡¥
¤³¤ì¤ÏÆ󳬾ïÈùʬÊýÄø¼°¤Ç¾¯¤·°·¤¤¤Ë¤¯¤¤¤Î¤Ç¡¤Â®ÅÙ v = du/dt ¤È¤¤¤¦¿·¤·¤¤½¾Â°ÊÑ¿ô¤òƳÆþ¤·¤Æ¡¤
¤È¤¤¤¦¤â¤Î¤ËÊÑ·Á¤·¤Æ¡¤¤³¤ì¤Ë¤Ä¤¤¤Æ¹Í¤¨¤è¤¦¡¥
¤³¤ÎÊýÄø¼°¤Ï¼ê¤Ç²ò¤±¤Æ¤·¤Þ¤¦¤¬¡¤¼ê¤Ç¸·Ì©²ò¤¬µá¤Þ¤é¤Ê¤¤¾ì¹ç¤Ë¤âÄÌÍѤ¹¤ë¹Í¤¨Êý¤È¤·¤Æº£²ó¤Ï¥×¥í¥°¥é¥à¤Ç¶á»÷²ò¤òµá¤á¤Æ¤ß¤è¤¦¡¥¤½¤ì¤Ë¤ÏÍÍ¡¹¤Ê¼êË¡¤¬¤¢¤ë¤¬¡¤º£²ó¤ÏºÇ¤âñ½ã¤Ê EulerË¡ ¤È¤¤¤¦¤â¤Î¤ò»È¤Ã¤Æ¤ß¤è¤¦¡¥
Euler Ë¡ †
Euler Ë¡¤È¤¤¤¦¤Î¤Ï´Êñ¤Ç¡¤»þ´ÖȯŸ¹à¤òÁ°¿Êº¹Ê¬¤Ç¶á»÷¤¹¤ë¤³¤È¤Ç¡¤¸Å¤¤»þ´Ö¤ÎÊÑ¿ôÃͤòÂåÆþ¤¹¤ë¤È¿·¤·¤¤»þ´Ö¤ÎÊÑ¿ôÃͤ¬½Ð¤Æ¤¯¤ë´Ø·¸¼°¤ËÌäÂê¤òÊÑ·Á¤¹¤ë¤â¤Î¤Ç¤¢¤ë¡¥
¤Þ¤¢¡¤ÍýÏÀ¤ò¸À¤¦¤è¤ê¸«¤¿¤Û¤¦¤¬Áᤤ¤À¤í¤¦¡¥
º£²ó¤Î¾ì¹ç¡¤»þ´ÖÊÑ¿ô t ¤ò ¢¤t ¤ÎÉý¤Ç¡Ö¹ï¤à¡×¤³¤È¤Ë¤·¤Æ¡¤¾å¤Î¾ïÈùʬÊýÄø¼°¤ò
¤È¤¹¤ë¤Î¤¬ Euler Ë¡¤Ç¤¢¤ë¡¥¤½¤·¤Æ¤³¤Î¼°¤ò¤¤ì¤¤¤Ë½ñ¤Ä¾¤¹¤È¡¤
¤È¤Ê¤ë¤Î¤Ç¡¤¤³¤ì¤ò¤ß¤ë¤È¡Ö±¦ÊÕ¤ËÃΤäƤ¤¤ëÃͤòÂåÆþ¤¹¤ë¤À¤±¤Ç¡¤¿·¤·¤¤»þ´Ö¤Ç¤ÎÃͤ¬ÆÀ¤é¤ì¤ë¡×·Á¤Ë¤Ê¤Ã¤Æ¤¤¤ë¡¥
¾ïÈùʬÊýÄø¼°¤ò¤³¤Î¤è¤¦¤Ë¶á»÷¼°¤ËÃÖ¤´¹¤¨¤ë¤Î¤¬ Euler Ë¡¤Ç¤¢¤ë¡¥
¤³¤ì¤Ê¤é¥×¥í¥°¥é¥à¤¬½ñ¤±¤½¤¦¤À¤È¤¤¤¦´¶¿¨¤¬ÆÀ¤é¤ì¤ë¤À¤í¤¦¡¥
![]() ¤â¤Á¤í¤ó¡¤Euler Ë¡¤Çºî¤Ã¤¿¡Ö¶á»÷¼°¡×¤ò²ò¤¤¤ÆÆÀ¤é¤ì¤ë¤Î¤Ï¡Ö¶á»÷²ò¡×¤Ç¤¢¤ê¡¤¤â¤È¤Î¾ïÈùʬÊýÄø¼°¤Î²ò¤Ç¤Ï¤Ê¤¤¡¥¤¿¤À¡¤¤½¤ó¤Ê¤Ë°ã¤ï¤Ê¤¤¤ó¤¸¤ã¤Ê¤¤¡© ¤È¤¤¤¦´üÂÔ¤ò¤¹¤ë¤È¤¤¤¦¤³¤È¤À¤Í¡¥
¤â¤Á¤í¤ó¡¤Euler Ë¡¤Çºî¤Ã¤¿¡Ö¶á»÷¼°¡×¤ò²ò¤¤¤ÆÆÀ¤é¤ì¤ë¤Î¤Ï¡Ö¶á»÷²ò¡×¤Ç¤¢¤ê¡¤¤â¤È¤Î¾ïÈùʬÊýÄø¼°¤Î²ò¤Ç¤Ï¤Ê¤¤¡¥¤¿¤À¡¤¤½¤ó¤Ê¤Ë°ã¤ï¤Ê¤¤¤ó¤¸¤ã¤Ê¤¤¡© ¤È¤¤¤¦´üÂÔ¤ò¤¹¤ë¤È¤¤¤¦¤³¤È¤À¤Í¡¥
ÌäÂêÀßÄê †
¤µ¤Æ¡¤¥·¥ß¥å¥ì¡¼¥È¤¹¤ë¤Ë¤Ï¶ñÂÎŪ¤Ê¾ò·ï¤òµÍ¤á¤Ê¤¤¤È¤¤¤±¤Ê¤¤¡¥
¤½¤³¤Ç¡¤°Ê²¼¤Î¤è¤¦¤Ë½é´ü¾ò·ï¤Ê¤É¤òÀßÄꤷ¤è¤¦¡¥
[½é´ü¾ò·ï]
½é´ü¹â¤µ u(0) = 1000.0 (m)
½é´ü®ÅÙ v(0) = 0.0 (m/s)
[½ªÎ»¾ò·ï]
¹â¤µ¤¬ 0 m°Ê²¼¤È¤Ê¤Ã¤¿¤é¥·¥ß¥å¥ì¡¼¥·¥ç¥ó½ªÎ».
[¶á»÷¾ò·ï]
»þ´Ö¹ï¤ßÉý ¢¤t = 0.1 sec
¥×¥í¥°¥é¥à †
![]() °Ê²¼¤ÎÉôʬ¤Ï¼Â½¬¤·¤Ê¤¬¤éÍý²ò¤·¤è¤¦¡¥
°Ê²¼¤ÎÉôʬ¤Ï¼Â½¬¤·¤Ê¤¬¤éÍý²ò¤·¤è¤¦¡¥
¥×¥í¥°¥é¥à¤Ï¾å¤Î¾ò·ï¤Ë½¾¤Ã¤Æ·×»»¤·¤Æ »þ´Ö, ¹â¤µ ¤Î¿ô»ú¥Ú¥¢¤ò½ÐÎϤ¹¤ë¤â¤Î¤È¤·¤è¤¦¡¥
¤¹¤ë¤È¡¤¤À¤¤¤¿¤¤°Ê²¼¤Î¤è¤¦¤Ê´¶¤¸¤Ë¤Ê¤ë¤À¤í¤¦¤«¡¥
¥×¥í¥°¥é¥à¤òÆ°¤«¤·¤Æ¥Ç¡¼¥¿¤òÆÀ¤ë †
¾å¤Î¥×¥í¥°¥é¥à¤ò¼Â¹Ô¤·¤Æ¡¤¥Ç¡¼¥¿¤òÆÀ¤è¤¦¡¥ÆÀ¤é¤ì¤¿¥Ç¡¼¥¿¤¬²èÌ̤Ëɽ¼¨¤µ¤ì¤ë¤À¤±¤Ç¤Ï¤¢¤Þ¤êÌò¤ËΩ¤¿¤Ê¤¤¤Î¤Ç¡¤¥Õ¥¡¥¤¥ë¤ËÊݸ¤·¤è¤¦¡¥
¤½¤ì¤Ë¤ÏÎ㤨¤Ð¡¤¾å¤Î¥×¥í¥°¥é¥à¥Õ¥¡¥¤¥ë̾¤¬ euler.rb ¤À¤È¤·¤Æ¡¤
ruby -w euler.rb > euler.dat
¤Ê¤É¤È¤·¤Æ¼Â¹Ô¤¹¤ì¤Ð¤è¤¤¡Ä¤Î¤Ï³Ð¤¨¤Æ¤¤¤ë¤Í¡© ¤³¤Î¾ì¹ç¡¤¥Ç¡¼¥¿¤¬ euler.dat ¤È¤¤¤¦¥Õ¥¡¥¤¥ë¤ËÊݸ¤µ¤ì¤ë¡¥
ÆÀ¤é¤ì¤¿¥Ç¡¼¥¿¤òÆ°²èŪ¤Ë¸«¤Æ¤ß¤è¤¦ †
¾å¤Î¥Ç¡¼¥¿¥Õ¥¡¥¤¥ë¤ò¸«¤Æ¤ß¤ë¤È¡¤Á´Éô¤Ç 144¹Ô¤¢¤ë¡¥¤½¤³¤Ç¡¤¤³¤Î 144¹Ô¤ò 1¹Ô¤º¤Ä gnuplot ¤Ê¤É¤Ç¸«¤Æ¤ß¤ì¤ÐÆ°²èŪ¤Ë¾õ¶·¤¬¸«¤é¤ì¤ë¤³¤È¤Ë¤Ê¤ë¡¥
¤½¤³¤Ç¡¤°Ê²¼¤Î¤è¤¦¤Ëºî¶È¤·¤Æ¤ß¤è¤¦¡¥
1) gnuplot ¤ÎÆ°ºî¥Õ¥¡¥¤¥ë¤òºî¤ë: euler.plt ¤È¤¤¤¦Ì¾Á°¤Î¥Õ¥¡¥¤¥ë¤òºî¤ê¡¤¼¡¤ÎÃæ¿È¤ò½ñ¤¹þ¤à¡¥
2) gnuplot ¤ÎÆ°ºî¥Õ¥¡¥¤¥ë¤òºî¤ë(1¹Ô¤º¤Äɽ¼¨¤¹¤ëÉôʬ): euler.loop ¤È¤¤¤¦Ì¾Á°¤Î¥Õ¥¡¥¤¥ë¤òºî¤ê¡¤¼¡¤ÎÃæ¿È¤ò½ñ¤¹þ¤à¡¥
3a) gnuplot (¥á¥Ë¥å¡¼ ¢ª Math ¢ª gnuplot) ¤òµ¯Æ°¤·¡¤
3b) ¾å¤Î¥Ç¡¼¥¿¥Õ¥¡¥¤¥ë euler.dat, gnuplot ¤ÎÆ°ºî¥Õ¥¡¥¤¥ë euler.plt, euler.loop ¤Î3¤Ä¤Î¥Õ¥¡¥¤¥ë¤¬ÃÖ¤¤¤Æ¤¢¤ë¥Ç¥£¥ì¥¯¥È¥ê¤Ë gnuplot ¤ÎÆ°ºî¥Ç¥£¥ì¥¯¥È¥ê¤ò¡Ö°ÜÆ°¡×¤µ¤»¤ë(¡Ö°ÜÆ°¡×¤È¤«¡ÖChDir¡×¤È¤«½ñ¤¤¤Æ¤¢¤ë¥Ü¥¿¥ó¤¬¤¢¤ë¤À¤í¤¦)¡¥
3c) gnuplot ¤ÎÌ¿Îá²èÌ̤Ç
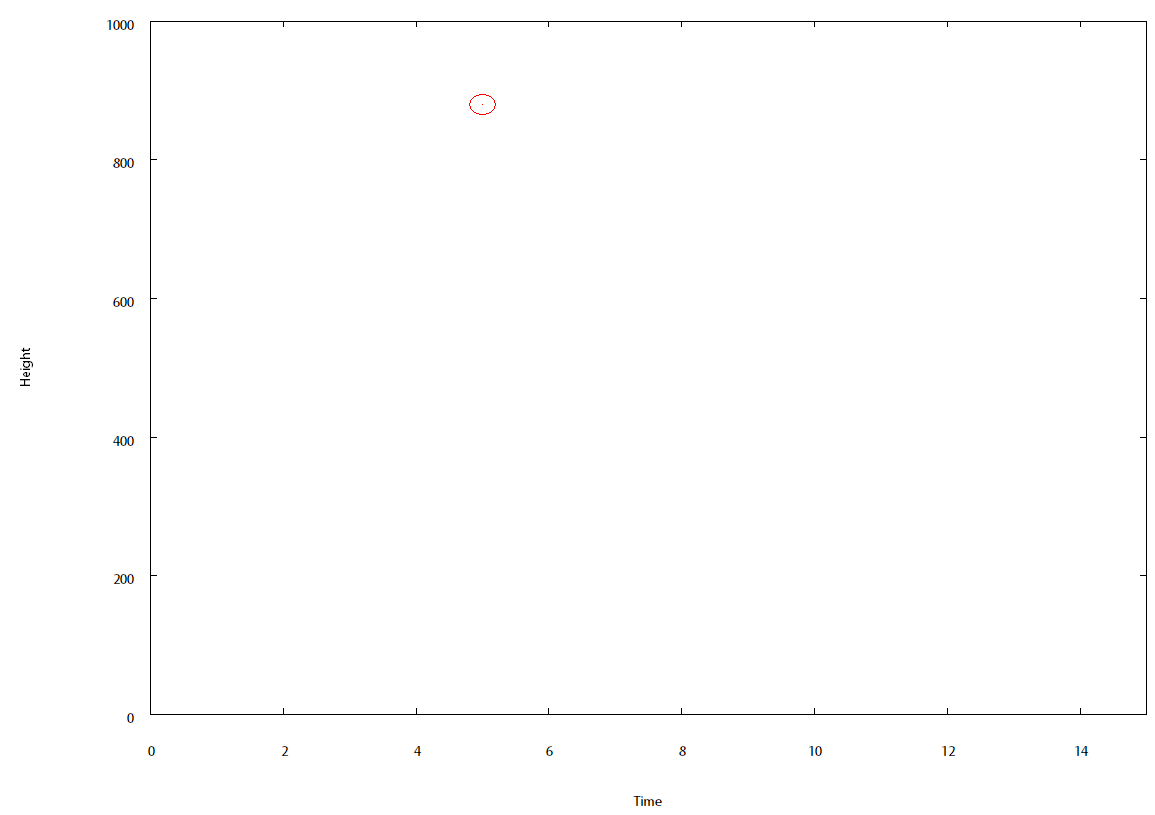
load "euler.plt"
¤ÈÆþÎϤ¹¤ë¡¥ÌäÂ꤬¤Ê¤±¤ì¤Ð¡¤°Ê²¼¤Î¿Þ¤Î¤è¤¦¤Êɽ¼¨¤ÇÆ°²èŪ¤Ë¤½¤Î¹â¤µ¤ò¼¨¤¹ ¡û °õ¤¬Æ°¤¤¤Æ¤¤¤¯¤Ï¤º¤À(²£¼´¤Ë»þ´Ö¤ò¤È¤Ã¤Æ¤¤¤ë)¡¥
![]() gnuplot ¤Ç1¹Ô¤º¤Äɽ¼¨¤ò·«¤êÊÖ¤µ¤»¤ë¤Î¤Ë»È¤Ã¤Æ¤¤¤ë¥Æ¥¯¥Ë¥Ã¥¯¤Ï¼ç¤Ë°Ê²¼¤ÎÆó¤Ä¤Ç¤¢¤ë¡¥
gnuplot ¤Ç1¹Ô¤º¤Äɽ¼¨¤ò·«¤êÊÖ¤µ¤»¤ë¤Î¤Ë»È¤Ã¤Æ¤¤¤ë¥Æ¥¯¥Ë¥Ã¥¯¤Ï¼ç¤Ë°Ê²¼¤ÎÆó¤Ä¤Ç¤¢¤ë¡¥
- reread : ¤³¤ì¤Ï¡¤¤½¤ÎÌ¿Î᤬Æþ¤Ã¤¿¥Õ¥¡¥¤¥ë¤òÆɤßľ¤¹¤È¤¤¤¦°ÕÌ£¤Ç¤¢¤ë¡¥if ¤ÈÁȤ߹ç¤ï¤»¤Æ Ruby ¤Î while ¤ß¤¿¤¤¤Ë»È¤Ã¤Æ¤¤¤ë¡¥
- plot Ì¿Îá¤Î¸å¤í¤Ë¤Ä¤¤¤Æ¤¤¤ë every ::line::line : ¤³¤ì¤Ï¥Ç¡¼¥¿¤ÎÂè line+1 ¹ÔÌܤΤߤòÆɤó¤Ç plot ¤·¤í¤È¤¤¤¦¤³¤È¤ò°ÕÌ£¤¹¤ë¡¥
![]() ¤¹¤Ù¤Æ¤Î½Ö´Ö¤Î²èÁü¤òÍÑ°Õ¤·¡¤¤½¤ì¤ò¤Ä¤Ê¤²¤ÆÆ°²è¤òºî¤ë¤È¤¤¤¦ÊýË¡¤â¤¢¤ë¡¥Í¾Íµ¤Î¤¢¤ë¤â¤Î¤Ï¤³¤Á¤é¤Ë¥Á¥ã¥ì¥ó¥¸¤¹¤ë¤Î¤â¤è¤¤¤À¤í¤¦¡¥¤Á¤Ê¤ß¤Ë¡¤²èÁü¤ò¤Ä¤Ê¤²¤ÆÆ°²è¤Ë¤¹¤ë¥½¥Õ¥È¥¦¥§¥¢¤È¤·¤ÆWindows ·Ï¤Ê¤é¤Ð
¤¹¤Ù¤Æ¤Î½Ö´Ö¤Î²èÁü¤òÍÑ°Õ¤·¡¤¤½¤ì¤ò¤Ä¤Ê¤²¤ÆÆ°²è¤òºî¤ë¤È¤¤¤¦ÊýË¡¤â¤¢¤ë¡¥Í¾Íµ¤Î¤¢¤ë¤â¤Î¤Ï¤³¤Á¤é¤Ë¥Á¥ã¥ì¥ó¥¸¤¹¤ë¤Î¤â¤è¤¤¤À¤í¤¦¡¥¤Á¤Ê¤ß¤Ë¡¤²èÁü¤ò¤Ä¤Ê¤²¤ÆÆ°²è¤Ë¤¹¤ë¥½¥Õ¥È¥¦¥§¥¢¤È¤·¤ÆWindows ·Ï¤Ê¤é¤Ð
- ¥¦¥£¥ó¥É¥¦¥º¥à¡¼¥Ó¡¼¥á¡¼¥«¡¼
(Âç³Ø¤ÎPC ¤Î¾ì¹ç: ¥á¥Ë¥å¡¼ ¢ª ¥×¥í¥°¥é¥à ¢ª ¥¢¥¯¥»¥µ¥ê ¢ª ¥Õ¥¡¥¤¥ë̾¤ò»ØÄꤷ¤Æ¼Â¹Ô ¢ª moviemk.exe ¤ÈÆþÎÏ ¤Çµ¯Æ°): Windows ¤ËÉÕ°¤Î̵ÎÁ¥½¥Õ¥È - TMPGEnc ̵ÎÁÈÇ
¤Ê¤É¤¬¡¤Unix ·Ï(´Þ¤à Mac)¤Ê¤é¤Ð
- ffmpeg
¤Ê¤É¤¬¤¢¤ë¤Î¤Ç(¼«Âð¤Ç¥¤¥ó¥¹¥È¡¼¥ë¤¬É¬Íפʤâ¤Î¤Ï¥¤¥ó¥¹¥È¡¼¥ë¤·¤Æ)»È¤Ã¤Æ¤ß¤è¤¦¡¥
º£Æü¤ÎÁí»Å¾å¤² †
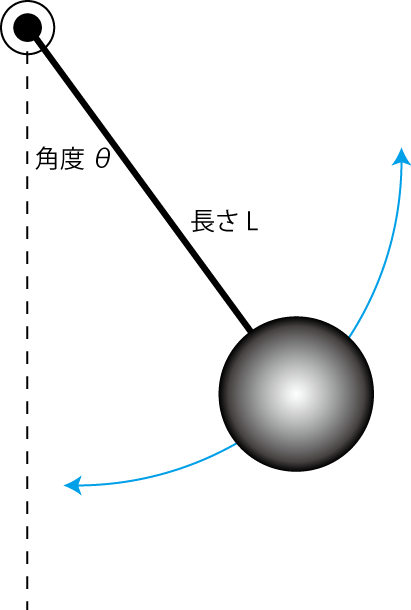
¾å¤ÎÎãƱÍͤˡ¤º£Å٤ϽÅÎϲ¼¤Ç Newton ¤Î±¿Æ°ÊýÄø¼°¤Ë±è¤Ã¤ÆÆ°¤¯¡Ö¿¶¤ê»Ò¤Î±¿Æ°¡×¤ò¥·¥ß¥å¥ì¡¼¥·¥ç¥ó¤·¤Æ¤ß¤è¤¦¡¥
¤Þ¤º¤Ï³Æ¾ò·ï¤ò°Ê²¼¤Î¤è¤¦¤Ë¤·¤Æ¤ß¤è¤¦¡¥
[¾õ¶·¾ò·ï]
¿¶¤ê»Ò¤Îɳ¤ÎŤµ L = 1.0 m
[½é´ü¾ò·ï]
½é´ü³ÑÅÙ θ(0) = π/3 (rad) = 60.0 (ÅÙ)
½é´ü®ÅÙ dθ/dt(0) = 0.0 (rad/s)
[½ªÎ»¾ò·ï]
t = 0 sec ¤«¤é³«»Ï¤·¤Æ¡¤³Æ¼«¼«Ê¬¤Ç·è¤á¤¿»þ´Ö t = T_limit (5.0¤°¤é¤¤?)¤Þ¤Ç¥·¥ß¥å¥ì¡¼¥·¥ç¥ó¤ò¹Ô¤¦.
[¶á»÷¾ò·ï]
»þ´Ö¹ï¤ßÉý ¢¤t = 0.01 sec (¾¯¤·¾®¤µ¤¯¤·¤Æ¤ª¤¤¤¿)
[¶á»÷ÊýË¡]
Euler Ë¡
![]() º£Å٤϶õ´Ö¤¬Æ󼡸µ¤ÎÌäÂê¤À¤¬¡¤»þ´ÖȯŸ¤¹¤ëÊÑ¿ô¤Ï¡Ö³ÑÅÙ¡×°ì¤Ä¤À¤±¤Ëµ¢Ãå¤Ç¤¤ë¡¥
º£Å٤϶õ´Ö¤¬Æ󼡸µ¤ÎÌäÂê¤À¤¬¡¤»þ´ÖȯŸ¤¹¤ëÊÑ¿ô¤Ï¡Ö³ÑÅÙ¡×°ì¤Ä¤À¤±¤Ëµ¢Ãå¤Ç¤¤ë¡¥
¤½¤³¤Ç¡¤¤Þ¤º¤Ï Newton ¤Î±¿Æ°ÊýÄø¼°¤ò³ÑÅÙ¤ËÂФ¹¤ë¾ïÈùʬÊýÄø¼°¤ËÊÑ·Á¤·¤è¤¦¡¥
¤½¤ì¤«¤é¡¤¾å¤ÎÎã¤Î¤è¤¦¤Ë¡¤½¾Â°ÊÑ¿ô¤ò¿·¤¿¤Ë²Ã¤¨¤ë¤³¤È¤ÇÌäÂê¤ò 1³¬¤Î¾ïÈùʬÊýÄø¼°¤ËÊÑ·Á¤·¤è¤¦¡¥
¤½¤¦¤¹¤ì¤Ð Euler Ë¡¤Ç¶á»÷Ū¤Ë²ò¤±¤ë¤À¤í¤¦¡¥
¤¢¤È¡¤¥×¥í¥°¥é¥à¤Î¥Ç¡¼¥¿½ÐÎÏ»þ¤Ë x, y ¤ÎÆ󼡸µ¤ÎºÂɸ¤ËÊÑ´¹¤·¤Ê¤¤¤ÈÆ°²è¤¬¸«¤¨¤Ê¤¤¤Î¤Ç¡¤¤½¤³¤Ïµ¤¤ò¤Ä¤±¤è¤¦¡¥
¾åµé¼Ô¸þ¤±(1) †
¡ÖÆó½Å¿¶¤ê»Ò¡×(°ì¤Ä¤á¤Î¿¶¤ê»Ò¤Ë¤µ¤é¤Ë¿¶¤ê»Ò¤¬¤Ö¤é²¼¤¬¤Ã¤Æ¤¤¤ë)¤Ë¤Ä¤¤¤ÆƱÍͤ˥·¥ß¥å¥ì¡¼¥·¥ç¥ó¤·¤Æ¤ß¤è¤¦.
¾åµé¼Ô¸þ¤±(2) †
Euler Ë¡¤Ç¤Ï¤Ê¤¯¡¤¸Åŵ Runge-Kutta Ë¡¤È¤è¤Ð¤ì¤ëÊýË¡¤Ë¤Ä¤¤¤ÆÄ´¤Ù¡¤¤³¤ì¤ò¶á»÷¤È¤·¤Æ»È¤Ã¤Æ¤ß¤è¤¦¡¥
¥ì¥Ý¡¼¥È †
ËÜÆü¼õ¤±¤¿¹ÖµÁ¤ª¤è¤Ó¹Ô¤Ã¤¿¼Â½¬¤Ë¤Ä¤¤¤Æ¡¤´Êñ¤Ë¤Þ¤È¤á¤¿Êó¹ð¤ò¤»¤è.
¤Þ¤¿¡¤Áí»Å¾å¤²¤ÎÉôʬ¤Ç¼«Ê¬¤Ç½ñ¤¤¤¿¥×¥í¥°¥é¥à¤òÊó¹ð¤»¤è.
¤â¤Á¤í¤ó³Æ¼«¤Î
- ½ê°(³ØÉô¡¤³Ø²Ê)
- ³ØÀÒÈÖ¹æ
- ³Øǯ
- »á̾
- Æü»þ
- ´Î¿´¤Î¥ì¥Ý¡¼¥ÈÆâÍÆ(ÆÀ¤¿Ãθ«¡¤ºî¶È¤Ë¤Ä¤¤¤Æµ¤¤Å¤¤¤¿¤³¤ÈÅù¤â)
¤ò½ñ¤¯¤Î¤ò˺¤ì¤Ê¤¤¤è¤¦¤Ë.
about Icons, ClipArts †
Some icons in this page are downloadable at ICONFINDER.
The "note" icon ![]() designed by Marco Martin is distributed with the LGPL licence,
designed by Marco Martin is distributed with the LGPL licence,
the "warning" icon ![]() designed by Alexandre Moore with the GPL licence
designed by Alexandre Moore with the GPL licence
and the "triangle" icon ![]() designed by Joseph North is distributed with the Creative Commons (Attribution-Noncommercial-Share Alike 3.0 Unported) licence.
designed by Joseph North is distributed with the Creative Commons (Attribution-Noncommercial-Share Alike 3.0 Unported) licence.
Some clip arts used in this page are downloadable at Open Clip Art Library.
We deeply appreciate their superb works. With licence, they describe that "the actual clipart content on open clipart library is Public domain" in the web.
źÉÕ¥Õ¥¡¥¤¥ë: