15(Final Lecture) -- Introduction to Experimental Mathematics II -- by D.Furihata

■ No.15 (2002.02.13) Final Lecture … 確率と偏微分方程式，その他

さて，今回で授業は最終回である. 全体としては，15回では教えきれなかった内容が非常に多く，また，その不足分をカバーすべく詰め込んだ回もあり，消化不良をきたした学生も多かったと思う.
そのためにも資料は web に全てこうして公開してあるので，分からない部分が多かった，という生徒はなるべく時間を見つけて理解に努めるとよいかと思う.
# 文系学科に所属していると，授業を通して科学的思考に直接触れる機会は理系学科よりも減ってしまうように思うかもしれないが，だからといってそうした能力が文系で不要だというのではない.
# むしろ，厳しい「現実」を相手にする, という意味では文系の人間の方がそうした能力を「実用として」「鋭い形で」必要とするのである.
# であるから，少しでも時間のある学生の身分のうちにそうした能力を身につけておくと良い.

# 要するに～，将来絶対損はしないからやっとけ(^-^). さて，今回は，前回の続きを見てから，残りの時間で少し無駄な話をしてみよう.

酔っぱらい親父と微分方程式: 連続極限

さて，前回は酔っ払い親父の行く先を漸化式で確率的に予想するところまで計算した. そこで，以前微分方程式 ←→ 漸化式をいききしたのを思い出して，今度も似たように解析してみよう.
その時は何をやったかというと，微分方程式 --(離散近似)--> 漸化式として，漸化式で計算することで微分方程式の性質を知ろうとするものだった. そこで今回は，その逆をやってみよう.
つまり，漸化式 --(連続極限)--> 微分方程式をやってみて，微分方程式を調べることでもとの確率に関する知見を得ようというのである.
これで何が嬉しいかというと，漸化式と異なり，微分方程式になってしまえば Δx や Δt が姿を消すため，こうした離散化量の影響が消え，「純粋に共通する性質だけが見えてくる」ということや，微分方程式の研究は漸化式のそれよりも進んでいるため，より優れた結果を得られる可能性が高いという点などが挙げられる. 方程式の形によっては厳密解が得られたりもする.
さて実際に何をやるのか，というと，

離散近似(前回): 連続 → 離散
連続極限(今回): 離散 → 連続

という図式でいくぞ，ということだ. ではどうやったらよいのだろう?
前回の酔っ払い親父大集合の図から考えた確率分布の漸化式は，

                 P(k-1,n) + P(k+1, n)
    P(k, n+1) = ---------------------,      k:場所(歩数), n:時間(分)        … 式(1)
                          2

というものだった.
# 後で考えやすいように，前回と違って場所の記号を k に変更している.
この式を冷静になって考え直すと，本来連続量である「空間」「時間」が歩数，分という単位で離散化されている，ということがわかる. だから，この単位を小さくしていく方向で考えればよいはずだ. そこでまず，次のような対応関係を考えて，連続量で考えられるようにしよう.


    場所:  x = k * Δx,     k: 歩数, Δx: 歩幅

    時間:  t = n * Δt,     n: 親父が動く回数, Δt: 親父の動く単位時間(^-^)

で，最終的に Δx → 0, Δt → 0 という感じに考えればよいだろう.
すると，(場所, 時間)=(x,t) での親父の存在確率分布を新たに p(x, t) と書くとすると，p(x,t) は P(k, n) 相当なので，上の漸化式は

                   p(x-Δx,t) + P(x+Δx,t)
    p(x, t+Δt) = -------------------------,    x:場所, t:時間
                              2

ということになるだろう.
さて，問題はここから Δx → 0, Δt → 0 を考えるに当たってどうしたらよいか，である. そのまま考えると，

    p(x±Δx,t) → p(x,t)  when Δx → 0,
    p(x, t+Δt) → p(x,t)  when Δt → 0

と考えて，p(x,t) = p(x,t) という当たり前の式が出てくるだけ，になってしまう. これでは何も得られないので，もう少し考えてみよう.
実は，上の(連続)極限は 0次近似と言って，もっとも「粗い」極限近似である. いつも無駄な近似だ，というわけではなくて，今回は 0次近似によって当たり前の式が出てきてしまった，ということである. まあ，たいがいはそうなんだが.

そこで，もう少し精密な近似を行ってみよう. こういうとき, 数学には次のようなかなり便利な道具がある.

■ Taylor の定理

関数 f(x) が適当に滑らかならば，つまり，例えば N回微分できるとして，点 x の近くで(⇔ 下に出てくる Δx が小さい)関数 f には次のような関係式が成り立つ.

                                           Δx²              Δx^m                    Δx^N
        f(x+Δx) = f(x) + f'(x)Δx + f"(x) --- + … + f^(m)(x) --- + … +f^(N)(x+αΔx) ---             (← Taylor 展開公式 とよばれる)
                                            2                 m!                     N!
                         d^mf |
        ただし，f^(m)(x) = --- | ,      0 ≦α≦1
                         dx^m |_x

これはどういう意味かというと，「場所がちょっとズレたところの関数値は，元の位置の微分値と場所のズレ量からだいたい計算できる」ということなのである.

ちょっと試しにやってみよう. sin(x) を，x = 0 の近くで展開してみると，

                                                 Δx²                Δx^m
        sin(Δx) = sin(0) + sin'(0)Δx + sin"(0) --- + … + sin^(m)(x) --- + …
                                                  2                   m!

となるが， sin'(x) = cos(x), sin"(x) = cos'(x) = -sin(x), … , と， sin(0) = 0, cos(0) = 1 から，上の式は

                         Δx³  Δx⁵  Δx⁷     Δx⁹
        sin(Δx) = Δx - --- + --- - ---- + ------ - …
                          6    120   5040   362880

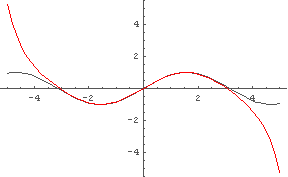
と書き換えられることになる. これがどれくらい信用できるか，Mathematica でチェックしてみよう.

    In[1]:= Needs["Graphics`"];    ← 必要になるので，一番最初に忘れないようにやっておく.
    In[2]:= Needs["Statistics`"];  ← これも必要になるかもしれないのでやっておこう.

    In[3]:= Tsin[x_] := x - x^3/6 + x^5/120 - x^7/5040       ← 上の Taylor 展開した式の 7次項までを採用してみた近似式.

    In[4]:= DisplayTogether[
              Plot[Sin[x], {x, -5, 5}], 
              Plot[Tsin[x], {x, -5, 5}, PlotStyle -> Hue[0]]
              ]
               ← 本物と近似式を両方 グラフにしてみると…
               ← x = 0 の近くでは十分近似できていそうだ.

今は 7次項まで使ってみたが，これを少なくしたり，多くしたりしたらどうなるかチェックしてみよ. → (授業中の課題)
sin(x) ではなく，cos(x) でやってみたらどうなるか? → (授業中の課題)
sin²(x) + cos²(x) = 1 という関係式が，Taylor 展開を使った近似式ではどれくらい正確に近似されるか，チェックしてみよ. → (授業中の課題)

さて，この Taylor 展開を手でやるのは結構面倒だ. 計算自体は決まり切った単純なものだけに，こういうことは機械にやらせたい. 幸い，Mathematica にはそういう機能があるので，それを使おう.

● Taylor 展開を行う … Series[関数, {変数, 中心, 最大次数}]
→ Series[ f[x], {x, a, n}] とすると，Δx = x-a と解釈して f(x) = f( a+Δx ) を a を中心に n 次項まで展開する. ← 挙動がちょっとわかりにくい.
→ まだ高次項があるよ～と教えるために，最後に剰余項(高次項表示)がつく. これは次の Normal 関数で除去できる.

● 特殊な形式の式を通常の式に変換する … Normal[式]
→ 例えば，べき級数式(高次項まで延々と存在する式)は， Normal[式] とすることで通常の n 次多項式に.

さて，どう使うのか実際にやってみよう.

    In[5]:= Series[Sin[x], {x, 0, 10}]  ← 中心が 0, ズレ Δx = x - 0 となるので…

                 x³    x⁵     x⁷      x⁹
    Out[5]= x - --- + --- - ---- + ------ + O[x¹¹]            ← 上で手でやったものと同じ式が得られた.
                 6    120   5040   362880
       
    In[6]:= Normal[%]

                 x³    x⁵     x⁷      x⁹
    Out[6]= x - --- + --- - ---- + ------             ← 最後の高次項が除去され，普通の式になった.
                 6    120   5040   362880
       
    In[7]:= TTsin[x_]:= %                             ← 普通の式だから普通に定義などに利用できる.
    
    In[8]:= Plot[TTsin[x], {x, -3, 3}]                ← ためしにこの近似式をプロットしてみると…
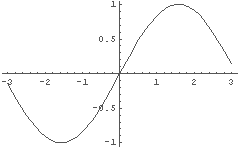               ← sin(x) に十分そっくり.

やはり sin(x) ではなく，cos(x) でやってみたらどうなるか? → (授業中の課題)
さて，Taylor 展開に親しんだところで，もとの話に戻ろう. この Taylor 展開を使って何をしようとしていたかというと，

    p(x±Δx,t) → p(x,t) + … when Δx → 0,
    p(x, t+Δt) → p(x,t) + … when Δt → 0

の … の部分をもちょっと詳しく求めようとしていたのだった. もちろん，手で計算するのが本筋だが，慣れるまでは大変かもしれないので，Mathematica にやってもらおう.
まず，p(x+Δx, t) を展開してみよう.

    In[9]:= Normal[Series[p[y, t], {y, x, 10}]]    ← x を中心に，Δx= y-x と考えて展開.
    Out[9]= p[x,t] + p^(1,0)[x,t] (y-x) + …略…

    In[10]:= % /. y -> x+dx                ← Δx= y-x, つまり y = x + Δx だというのを代入.
    Out[10]= p[x,t] + dx * p^(1,0)[x,t] + 1/2 dx² p^(2,0)[x,t] + …略…
                                           ← これが，p(x+dx, t) を展開したもの，になる.

       ただし，途中の p^[1,0][x,t] などの表示は，
                     ∂¹   ∂⁰
       p^[1,0][x,t] = ---   ---   p[x,t] 
                     ∂x¹  ∂t⁰
       という意味である.

さて，これで p(x+dx, t) がどう展開されるか，は計算できた. 毎回これでは面倒なので，p(x+dx, t+dt) を展開する関数を作ってしまおう.
# 展開次数も決められるようにして…

    In[11]:= TS[f_, x_, dx_, t_, dt_, n_] := Normal[
               Series[
                 Series[f[y, z], {y, x, n}] , 
                 {z, t, n}
                 ]
               ] /. {y -> x + dx, z -> t + dt} // Expand
               ← 式を最終的には展開しておく.

    In[12]:= TS[f, x, dx, t, dt, 1]      ← 例えば，f(x+dx, t+dt) を 1次までで展開すると…

    Out[12]= f[x,t] + dt f^(0,1)[x,t] + dx f^(1,0)[x,t] + dt dx f^(1,1)[x,t]
                                         ← こういう展開(近似)式が得られる.

さて，改めてこの TS という関数を用いて，p(x±Δx,t), p(x,t+Δt) を展開して代入してみよう.

    In[13]:= rhs1 = TS[p, x, -dx, t, 0, 4]    ← 右辺第一項，つまり p(x-dx, t) の展開. 4次までやっている.
    Out[13]=  p[x,t]-dx p^(1,0)[x,t]+(1/2)dx²p^(2,0)[x,t]-(1/6)dx³p^(3,0)[x,t]+(1/24)dx⁴p^(4,0)[x,t]

    In[14]:= rhs2 = TS[p, x, dx, t, 0, 4]     ← 右辺第二項，つまり p(x+dx, t) の展開.
    Out[14]= …略…

    In[15]:= rhs = (rhs1 + rhs2)/2 // Simplify  ← 右辺をもう計算してしまえ.
    Out[15]= p[x,t] + (1/2)dx²p^(2,0)[x,t]+(1/24)dx⁴p^(4,0)[x,t]


    In[16]:= lhs = TS[p, x, 0, t, dt, 4]     ← 左辺，つまり p(x,t+Δt).
    Out[16]= p[x,t]+dt p^(0,1)[x,t]+(1/2)dt²p^(0,2)[x,t]+…略…

さて，この展開式を用いれば，親父挙動の漸化式を近似する微分方程式が得られそうだ. しかし，展開の項は何次までとればよいのだろう?
それは，最終的に Δx → 0, Δt → 0 を考えていることから，式の両辺の展開式のうち，0次近似項(p[x,t])と，その次の項までとれば，まずはよい. なぜなら，それより高次の項は，今とった項より先に速やかにゼロに近づくからである.
# つまり，ここが「連続極限 Δx → 0, Δt → 0 の操作」を本質的に行っている，と見てよい.

           p(x-Δx,t)+p(x+Δx,t)                 1
   (右辺) ----------------------   →  p(x,t) + --- p^(2,0)(x,t) * Δx²   when Δx → 0,
                     2                           2

   (左辺)  p(x, t+Δt)             →  p(x,t) + p^(0,1)(x,t) * Δt        when Δt → 0

となるので，これより左辺 = 右辺の式を作ると,

    ∂p    Δx²   ∂²p
    --- = -----  ------
    ∂t    2Δt   ∂x²

という「偏微分方程式」になる. つまり，これが「上の漸化式を最も粗いレベルで近似する微分方程式」ということである.
実は，これは物理で言う「拡散現象」の一番典型的なモデル方程式なのである. つまり，

「酔っ払い親父の挙動は拡散現象だった」

ということが(近似ではあるが)いえる，ということである.

これで，あとは残った Δx, Δt を含む部分が Δx → 0, Δt → 0 の時にどうなるか，を考えればよい.
これは，発想を逆にすると分かりやすい. つまり，上の漸化式は，もともと

                            ∂p      ∂²p                       Δx²
    (親父の挙動微分方程式)    --- = γ ------,       ただし，γ = -----        … 式(2)
                            ∂t      ∂x²                       2Δt

という偏微分方程式を離散近似したものだ，と考えるのである. つまり，γ は固定されている，と考えればよい.
# 固定されているが，その値は自分で好きに決められる.

例えば，今回の問題は，最初の問題，つまり酔っ払い親父の挙動を考えるときは Δx = 1, Δt = 1 で考えていたとみなすならば， γ= 1/2 あたりに固定するのが適当そうだろう.

その代わり，γ を固定したので，Δx，Δt は上の関係式を満たさねばならない，と考えればよい. つまり，今回は γ = 1/2 としたのならば

                        Δx²
   (離散化量の制限式)    --- = 1
                        Δt

が， Δx と Δt が満たすべき関係式で，それを満たす範囲で動ける，ということになる.
少々ややこしいかもしれないので，全体を整理してみよう. 今のところ，我々が得た知見は以下のように図式化できる.

微分方程式と漸化式の関係
偏微分方程式 p_t = (1/2) p_xx の解 p(x,t)	<------------ 近似になっているはず ------------> (Δx, Δt が小さいほど良い近似)	漸化式式(1) の解 P(k,n)
	満たすべき関係式 x = k Δx, t = n Δt, Δx²/Δt = 1

さて，この関係は本当に正しいだろうか. 確認してみよう. そのために，偏微分方程式を解く必要があるが，ここは一つ Mathematica に頑張ってもらうことにしよう.
実はこの偏微分方程式は手で厳密解が得られる. が，その解説をするには余りに時間が足りない(^-^).

まず，x ∈ [-4, 4] 程度を考えて，親父が最初は x=0 に確率 100% で存在する，という初期値で考えよう. するとその初期分布は連続な確率分布関数 p(x,0) として次のような関数で近似すればまあまあといえるだろう.

    In[17]:= OyajiIni[x_] := If[(-0.5 <= x )  && (x <= 0.5), 1, 0]     

    In[18]:= Plot[OyajiIni[x], {x, -5, 5}]
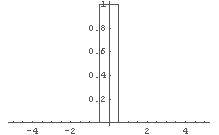               ← 親父が真ん中にいることがわかる.

この時の気をつけるべきポイントは，

親父の存在確率を全部積分すると 1 (=100%) になる.
確率が 0 付近に集中している.
確率分布の 0 付近への集中具合いが極端でない.

となる. 最初の二つは当たり前だが，最後のものはなぜか，というと，確率分布の集中具合いが極端になればなるほど，Mathematica にさせるものをはじめ，数値計算が難しくなるからである.
# 中心極限定理を考えると，初期値分布形状の少々の違いはすぐ影響なくなるはず，という読み(^-^)，もあるが.

さて，初期値はこんな感じで用意して，実際に Mathematica に偏微分方程式を解いてもらおう.
# ただし，偏微分方程式の数値計算は簡単なものでも負荷が簡単に増大するので，注意が必要だ.
# 具体的には，空間，時間領域の大きさを小さくとるなど，パラメータは控え目にしないといけない.
# でないと，精度よい計算ができないか or 計算量が多すぎて計算が終わらない，ということになる.

    In[19]:= NDSolve[
               {
                 D[p[x, t], t] == (1/2)* D[p[x, t], {x, 2}] , 
                 p[x, 0] == OyajiIni[x],
                 p[-4, t] == p[4, t]
                 },
               p, 
               {x, -4, 4}, {t, 0, 10}
               ]
                                 ← こうやって，必要な条件を突っ込んで解く.
                                    最初の式は，偏微分方程式そのものである.
                                    次の式は，初期値.
                                    その次の式は，境界条件である.
                                    (この境界条件は，周期的境界条件といって，境界が互いに繋がってループしている，と考えるものである.)
                                    実際に計算させると，精度が稼げないので Mathematica がいろいろと文句を言ってくる.

    Out[19]= {{p -> InterpolatingFunction[{{..., -4., 4., ...}, {0., 10.}}, <>]}}
                                 ← 補間関数への置換ルールとして答えが出力される.

    In[20]:= sol = %[[1,1,2]]    ← 答えの補間関数だけを取り出して使おう.

    In[21]:= Plot[ sol[x, 1], {x, -4, 4} ]  ← 例えば，t=1 の時の確率分布 p(x,1) はどうなっているかというと…
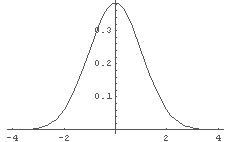             ← きれいに分布しているうえ，どこかでやはり見た図に．

    In[22]:= Plot3D[ 
               sol[x, t]  ,{x, -4, 4}, {t, 0, 10}, 
               PlotPoints -> 50, 
               PlotRange -> All
               ]
                                   ← さらに 3 次元図でも出力してみる.
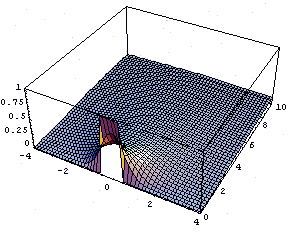               ← 初期のすぐ後に波形が丸まっているのがなんとなく分かると思う.

ただし，計算の途中で次のような新出の関数を用いている.

● 微分方程式の解を求める … NDSolve[{満たすべき条件}, 解となる関数, 変数の範囲]
→ 満たすべき条件式には，等号部分は = ではなくて == を使うことに注意.
→ 条件が足りなかったり，矛盾していたり，多すぎたりすると警告がでる.
→ 解は，(数値的な)補間関数への置換ルールとして出力される.
よって，使いたければ，上の例のように出力の [[1,1,2]] 要素を抽出して使った方が使いやすいか.
→ きちんと使いこなすには，精度やステップ数を自分で設定しないといけないが，計算時間がすごくかかることを考えると，どちらにしろあんまり本格的な目的には向かない印象がある.

● 微分する … D[関数, 変数]
→ D[f, x] は ∂f/∂x を出力する.
→ D[f, {x,n}] で ∂ⁿf/∂xⁿ となる.

● 関数の3次元グラフを描く … Plot3D[関数, 範囲]
→ 使い方は Plot と変わらない. 変数の数が 2 になっただけ.
→ ● グラフを描くのに使う点数を指定する … オプション PlotPoints

を使って，ある程度細かい図を描いている.

さて，これで偏微分方程式の解も求まったので，漸化式の解と比較してみよう.
比較のために，例えばパラメータを Δx = 1/10, Δt = 1/100 として，微分方程式の解で t = 1 とすると，漸化式の解で対応するのは n = 100 の時なので各々のグラフを出力してみて比較しよう.
偏微分方程式の解のグラフは既に上にあるし，漸化式のは前回用いた RWdist[a, 100] として，結果の [[-1]] 成分を使えばよい. すると，次のようになる.

偏微分方程式の解と漸化式の解の比較
偏微分方程式の解中央の高さ: 約 0.4 x の幅: 約 6 程度 t: 1	<------ 近似のはず ------> Δx = 1/10 Δt = 1/100 x = k Δx t = n Δt Δx²/Δt = 1	漸化式の解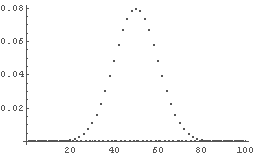中央の高さ(実質): 約 0.04 ↑ 値の半分は 0 なので，実質値は平均をとって約半分になる k の幅 : 約 60 程度 n : 100

これで，前回導入した漸化式が，偏微分方程式と(離散近似|連続極限) の関係にあることが確認できた，といえよう. これは何を意味しているか，というと，
「確率現象と偏微分方程式が繋がった」
ということである. も少し言うと，中心極限定理と偏微分方程式の解の間に何か関係があることをこの事実は示唆している.

また，上の偏微分方程式は「物質や熱の拡散のモデル方程式」として良く知られている，という事実を用いて物理的な言い方をすれば，
「拡散現象は，確率的な側面からも偏微分方程式の側面からもとらえられる」
ともいえる.

# さらに先のことを言えば，次のような関係がある… といってよいか. この関係を直接示すのはちょっと面倒だが，直感的には分かるだろう.

弱い解						強い解
偏微分方程式 (Fokker-Planck 方程式)	<---- (抽象) ----	確率分布の漸化式	←	確率事象	→	個々の事象の変化の様子	---- (抽象) ---->	確率微分方程式

ライフゲーム

さて，おまけとしてちょっと異なる趣向のものを見てみよう. ここでは，J. H. Conway が 1970年に考案した「ライフゲーム」について調べてみよう.
# ゲームといっても，遊びという意味ではなく，「ルールにしたがって状況が変化するシステム」という意味であるので間違えないよう(^-^).

ライフゲームは，2次元に格子状に白か黒色に変化する「セル」を配置して，次のようなルールで一斉にセル全部を変化させ，その変化の様子をみる，というものである.
これを，黒色のセルに数字 1 を割り当てて「生きている」と呼び，白色のセルに数字 0 を割り当てて「死んでいる」と呼んで，生物の挙動を再現するようなもの，と Conway は考えたのである.
さて，そのライフゲームのルールからまず見てみよう.

■ ライフゲームのルール(2値を 0,1 で表わす)
セルの新しい値 =	変化せず (現状維持)	周囲8セルの合計値 = 2 の場合
	1 (生まれる, 生き残る)	周囲8セルの合計値 = 3 の場合
	0 (死ぬ, 死んだまま)	その他

# この8つのセルからなる近傍を「ムーア近傍」という.

さて，こうしたライフゲームなるものを考えたときに，生じる疑問は以下のようなものである.

この単純なルールからどれくらい複雑な現象が起きるのか
→ 単純な離散方程式がどれだけ豊かな内容を含んでいるか。
初期状態がどう変化するか一般的に予測できるか
→ 局所的には決定されていて予測可能だが，巨視的にはどうか。
無限に発展するような初期状態は存在するか
→ 離散方程式としてみたとき，解の存在範囲は有界か
巧みに初期状態を設定することで知的なふるまいをするようなパターンを生成できるか
けして発展した結果としてありえないパターンはあるか

さて，これらの疑問を少しでも解明すべく，いろいろやってみよう. そのために，まずはライフゲームを Mathematica 上で実現しよう.
# ルールは簡単だが，Mathematica で綺麗にプログラムするのは難しい…

    In[23]:= TriIdentity[num_] := Apply[Plus, Map[RotateRight[IdentityMatrix[num] , #]&,{1,-1,0} ]]
                                                   ← 拡張三重対角(単位)行列を作る関数.
    In[24]:= TriIdentity[10] // MatrixForm         ← 例えば，これは…
    Out[24]//MatrixForm= 
         {{1, 1, 0, 0, 0, 0, 0, 0, 0, 1},
          {1, 1, 1, 0, 0, 0, 0, 0, 0, 0},
          {0, 1, 1, 1, 0, 0, 0, 0, 0, 0},
          {0, 0, 1, 1, 1, 0, 0, 0, 0, 0},
          {0, 0, 0, 1, 1, 1, 0, 0, 0, 0},
          {0, 0, 0, 0, 1, 1, 1, 0, 0, 0},
          {0, 0, 0, 0, 0, 1, 1, 1, 0, 0},
          {0, 0, 0, 0, 0, 0, 1, 1, 1, 0},
          {0, 0, 0, 0, 0, 0, 0, 1, 1, 1},
          {1, 0, 0, 0, 0, 0, 0, 0, 1, 1}}

    In[25]:= Moore[a_] := Module[{dim, A, result},
               dim =  Dimensions[a][[1]];
               A = TriIdentity[dim];
               result = A . a . A - a;
               Return[result]
               ]
             ← 上で作った行列を使ってこうすることで，ムーア近傍(自分除く)の 1 の数を数えることができる.
                # どうしてそうなるのか考えてみよ.
                ためしにやってみると，

    In[26]:= ( a = Table[Random[Integer], {5}, {5} ] ) // MatrixForm
    Out[26]//MatrixForm= 
         {{1, 1, 1, 0, 1},
          {1, 0, 0, 1, 0},
          {1, 0, 1, 1, 1},        ← ランダムに 0 or 1 をもつ行列を作っておいて，
          {0, 1, 0, 0, 1},
          {0, 1, 0, 0, 1}}

    In[27]:= Moore[a] // MatrixForm
    Out[27]//MatrixForm=
         {{5, 4, 3, 4, 4},
          {5, 6, 5, 5, 7},
          {4, 4, 3, 4, 5},        ← 計算してみると確かに.
          {6, 3, 4, 5, 4},
          {7, 4, 4, 4, 3}}

    In[28]:= new[1,2]:= 1;
    In[29]:= new[_,3]:= 1;
    In[30]:= new[_,_]:= 0;     
                                  ← new[今の値, ムーア近傍値] でライフゲームのルールに沿って新しい値が求まるように.

    In[31]:= SetAttributes[new, Listable]    ← こうすると，new[行列, 行列] で各々の要素に作用するようにできる.

    In[32]:= LGone[a_] := new[a, Moore[a]]   ← 行列を入れるとライフゲーム一回分更新したものを出力.

    In[33]:= LGone[a] // MatrixForm          ← ためしにさっきの行列 a に対してやってみると…
    Out[33]//MatrixForm= 
         {{0, 0, 1, 0, 0},
          {0, 0, 0, 0, 0},
          {0, 0, 1, 0, 0},
          {0, 1, 0, 0, 0},
          {0, 0, 0, 0, 1}}

    In[34]:= LG[init_, num_] := NestList[LGone[#] &, init, num]    ← ライフゲーム num 回分更新.

    In[35]:= LGplot[a_] := Show[
                Graphics[
                  RasterArray[
                    Reverse[a]  /. {1 -> GrayLevel[0.1], 0 -> GrayLevel[0.7]} 
                    ]
                  ],
                AspectRatio -> Automatic
                ]
                                                     ← 入力した行列を絵にして見せる.
                                                        黒っぽいところ… 1(生き), 白っぽいところ…0(死に)

    In[36]:= LGplot[a]                           ← ためしにこれも a にたいしてやってみると…
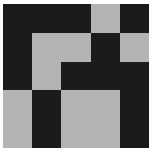             ← 確かに行列の通りに. Out[26] と比べてみれば分かる.

    In[37]:= LGanime[init_, num_] := Module[{a = init, b},
               LGplot[a];
               Do[
                 b = new[a, Moore[a]];
                 LGplot[b];
                 a = b,
                 {num}
                 ]
               ]
                  ← num 回分の絵を続けて出力. アニメーション用.

    In[38]:= LGanime[a, 10];      ← これも試してみる.     
            …略…                ← 11 枚のグラフが出力されるので，
                                     適当なグラフをダブルクリックすればアニメーションが見られる.

    In[39]:= LGinitR[num_] := Table[Random[Integer], {num}, {num}]
                                  ← 乱数によって初期値用に行列を作る.

    In[40]:= LGanimeR[dim_, ite_] := LGanime[ LGinitR[dim], ite ];
                                  ← 乱数による初期値でもって，ライフゲームを発展させたグラフをずずずいっと.

ただし，途中で以下のような関数を用いている.

● 中身を右へずらす … RotateRight[式, ずらし量]
→ RotateRight[{a,b,c,d}, 1] とすると，{d,a,b,c} が出力される.

● 単位行列を作る … IdentityMatrix[次元]
→ IdentityMatrix[3] とすると，

        {{1, 0, 0},
         {0, 1, 0},
         {0, 0, 1}}

が出力される.

● 式の次元を出力 … Dimensions[式]
→ まあ，要素数(のリスト)である.
例えば，Dimensions[{{a,b,c},{d,e,f}}] とすると，{2,3} が出力される.

● ベクトルや行列，テンソルの積 … Dot[引数] もしくは引数 . 引数

      → 行列 A と ベクトル b を

           {{a, b, c},              {j,
       A =  {d, e, f},       ,  b =  k,      とすると…
            {g, h, i}}               l}

               {aj+bk+cl,
       A . b =  dj+ek+fl,
                gj+hk+il}

       となる.

● マッチングの優先順位 … _ に関して複数通りのマッチングがある時
→ マッチング( _ )に関しては，「複数のマッチングがあり得る時は，より特定，特殊なマッチングが優先される」というルールがある. 例えば，上の new[,] という関数に対して上の定義だと
new[1,3] は new[_,3] と new[_,_] の 2通りのマッチングがあり得るが，より細かく定義されているnew[_,3] の定義が採用され，1 が出力になる.

● 関数: リスト要素の各個への作用属性 … Listable
→ 関数の属性. この属性がある関数 p は，p[ {a,b,c} ] とすると {p[a], p[b], p[c]} という出力を出してくれる. 便利. SetAttributes でこの属性を持たせることができる.

● 関数に属性をセットする … SetAttributes[関数, 属性]
→ 関数にある属性を持たせたいときに使う. 詳しくは，いろいろ調べてみるべし.

● グラフィック指示子の表を用いて 2次元縞模様を描く … RasterArray[表]
→ 要するに，表 { g_i,j }_i,j=1^n,m を用意するのだが， g_i,j はどんな色にするかという指示子， GrayLevel, RGBColor, Hue のいずれかにする.

● グラフ:白黒の濃淡を指示する … GrayLevel[数字]
→ 0 ～ 1 の間で(白黒)濃淡を指定し，それでグラフを描かせる. 0 が黒， 1 が白になる.

● 順序を逆にする … Reverse[式]
→ Reverse[ {a,b,c} ] は {c,b,a} になる.
上の RasterArray 等でグラフを描くとき，行列の見た目と絵が反転してしまうことがあるので，そうならないようにこれを使う.

さて，まずは大量に実験をして試してみるのがよいかと思うので，いろいろやってみよ. そのためにはまず，上に用意した LGanimeR[次元数, 時間数] を適当に使えばよい.

この次元数をちょっと大きめにして，何か知見が得られないか，いろいろ見てみよ. → (授業中の課題)

さて，このライフゲームについては，かつて非常に大勢の人間が(面白さゆえに)取り組み，その結果，非常に面白いパターンが数多く見つかっている.
その中からいくつか示しておこう. 各々のパターンに対し，どのような挙動が考えられるか，想像せよ. また，実際に試してみて，想像とあっていたか，違っていたか，違っていたならばその理由について考えてみよ.

R-ペントミノ　　パルサー　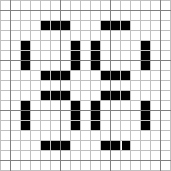　グライダー
グライダー銃

ちなみに，R-ペントミノを入力してみたりするには，例えば次のようにする.

    In[41]:= a = Table[0, {20}, {20}];

    In[42]:= a[[9,10]] = 1
    In[43]:= a[[9,11]] = 1
    In[44]:= a[[10,9]] = 1
    In[45]:= a[[10,10]] = 1
    In[46]:= a[[11,10]] = 1

ただ，これだと「盤」が狭すぎてすぐ発展の様子が分からなくなるので，もう少し大きな「盤」を用意した方が良い.

なお，ちょっとライフゲームについて調べてみたくなったならば， Mathematica では何かと不便である. そこで， http://psoup.math.wisc.edu/Life32.html にある Life32 などを用いるとよい. (これは windows 専用だが，非常に良くできている) 同 web には非常に多くのパターン集も集められているので，それを見ることで信じられないほど様々な現象があることが直感的に理解できるだろう.

ライフゲームとコンピュータ

実は，グライダー銃を巧みに配置することで，ライフゲーム上に AND 回路, OR 回路，NOT 回路を作ることができることが判明している.
# 電気パルスが行き来する代わりに，グライダーが行き来する.

これは，ライフゲームのパターンが汎用コンピュータになりうる，ということを示している.

これによって，コンピュータのプログラムに関する問題

■ (プログラム)停止問題

次のようなプログラム halt(p, x) と contrary(p) を考えよう.
ただし，入力時において，プログラムは文字列でもあるものとする.

halt(p,x) and contrary(p)
名称	入力	動作	出力
halt	プログラム p, 文字列 x	プログラム p に文字列 x を入力したときプログラム p が最終的にきちんと停止するかどうかを判断する.	p が停止すると判断できたら， yes p が停止しないと判断できたら， no
contrary	プログラム p	まず，answer = halt(p, p) とする. answer が yes ならば，暴走! answer が no ならばただちに停止する.	-

さて，このとき，

contrary(contrary) はどう動作するかわかるか?

というのが停止問題である.
さあ，考えてみよ．

から，導かれる「プログラム停止判定不能定理」から，

「ライフゲームの初期値がどのように長期的に変化していくか，一般に知る方法は実際にライフゲームを計算する以外にない」

ことが導かれる. これはどういうことか? というと，「ライフゲームは大域的予測不可能」ということである.

しかし，証明できるとはいえ，こんな簡単なルールに沿って発展するシステムの将来が予想できない，というのは常識からいえば非常に奇妙なことだ.

ライフゲームと人工生命理論

さらに，ライフゲームにはもう一つ大きな特徴がある. それは，ライフゲーム上には，

「自己複製する非常に複雑なパターンが存在する」

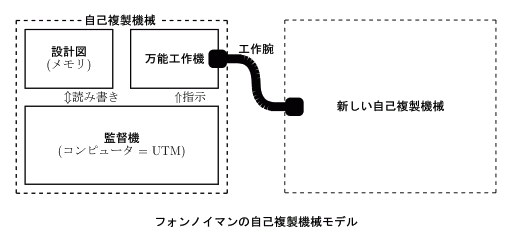
ということである. これは，結晶がその構造から同じ構造を他に作っていく，というものとは違い，自らの設計図(遺伝子に相当する)に沿って，他の個体を作り，設計図をコピーし，起動する，という手順で自己を複製するのである.
この発見(というかフォンノイマンらによる作成だが)によって，

自己複製という性質は科学的に実現できる = 「生命の神秘」などに帰する必要はない

ということが言えるようになった. 生命機械論はもちろん現在主流の考え方ではあるが，この発見がなされるまでは「生物は自己複製できるが，そういう機械は存在しない」という生命神秘派の主張を崩すことはできなかったのである.

>> 目次