ここでは注目する量が時間変化をする場合，
その変化をどうやって考察するか，を考えよう．
そのために最も簡単な方法の一つに「微分方程式」を作り，
作った微分方程式を調べるという方法がある．
そこで，ここでは微分方程式を作り簡単に調べるという一連の流れを
Mathematica を使って簡単に行ってみよう．
まず，注目する量が時間 t の関数 u(t) として書ける場合を考えよう． おおざっぱに言って，u(t), du/dt (← u(t) の t による微分)， d2u/dt2 (← u(t) の t による2階微分)， d3u/dt3, ... で方程式が作れるとき，これを常微分方程式という． 数式で書けば，
F(u, du/dt, d2u/dt2, d3u/dt3, ... ) = 0
と一般に書かれる，ということだ．
さて，この中で最も単純な形の
du/dt = G(u) ← 常微分方程式の正規形，と言われる．
というものについて考察してみよう．
→ 実は，普通の常微分方程式は形式的には全て正規形に直せる．
m 階微分 dmu/dtm まで含まれているとしたら，
新たに時間 t の関数を m 個用意して →
{uk(t)}, k=0,1,2,..m-1 と書くとして，
u0 := u,
u1 := du0/dt, ← = du/dt であることに注意．
u2 := du1/dt, ← = d2u/dt2 であることに注意．
：
um-2 := dum-3/dt, ← = dm-2u/dtm-2 であることに注意．
um-1 := dum-2/dt ← = dm-1u/dtm-1 であることに注意．
と定義して，F の(一種の)逆関数 F~ を
F(a0,a1,a2,.., am) = 0
⇔
am = F~(a0,a1,a2,.., am-1)
と定義する．すると，もとの方程式は
d(u0, u1,..., um-1)/dt
=
(u1, u2,..., um-1, F~)
という正規形に等しいことがわかる．
実際には F~ が形式だけでなく本当に定義できるかどうかが問題なわけだが…
さて，次のような問題を考えてみよう． あるバクテリアがかなりの勢いで増えていくとする． その増殖率を調べてみると，100万匹いる時，どうやら1秒あたりで 9531匹 だけ増えるようだった． 寿命や病気で死んだりする分は考えないとすると，時間 t (秒)でのこのバクテ リアの数を u(t) とすると，その変化は最も単純に考えると
du/dt = 9531/1000000 u = 0.009531 u ← 要するに，増える分 = du/dt とみなしている
という微分方程式で近似できる，と考えられる．
→ こういう風に，現象を数学的な式で置き換えて考えることをモデリングと言い，
あらゆる学問で重要な作業である．
いいかえると，現象に対して「数学を用いて仮説をたてる」こと，と言ってもよい．
これがきちんとできれば研究者として一人前，と言ってもよい… かな．
さて，この微分方程式から答えをどうやって求めたらよいだろう．
最も単純な方法論は，この微分方程式を数学的に厳密に解く，というものだが，
この授業は数学理論の授業ではないので，この方法論はパスせざるを得ない．
→ Mathematica に厳密に解かせる方法はある．
気になる者は，ヘルプ等で DSolve というコマンドについて調べてみよ．
さて，では次に単純な方法論はというと，微分方程式の
微分を単純な変化(=差)，で近似してしまうというものである(こういう近似を一般に
離散近似と呼ぶ)．
これは理論的に言うよりも見た方が早いだろう．
例えば，微少な時間 Δt が経過した時の微分を
u(t+Δt) - u(t)
du/dt ≒ -----------------
Δt
と近似して，上のバクテリアの変化を表す微分方程式を近似すると，
u(t+Δt) - u(t)
----------------- = 0.009531 u(t) ⇔ u(t+Δt) = (1 + 0.009531Δt) u(t)
Δt
となり， よりわかりやすく書けば，un := u(nΔt) と書くとして，
un+1 = (1 + 0.009531Δt) un
となる．
つまり，
離散近似によって常微分方程式が漸化式に変形される．
これならこれまでに学習したことを使っていろいろなことが調べられる．
例えば，最初に 100匹 のバクテリアがいたとすると，
Δt秒後には u1 = 100 * (1+0.009531Δt) 匹，
2Δt秒後には u2 = 100 * (1+0.009531Δt) * (1+0.009531Δt) 匹，
3Δt秒後には u3 = 100 * (1+0.009531Δt) * (1+0.009531Δt) * (1+0.009531Δt) 匹，
：
nΔt秒後には un = 100 * (1+0.009531Δt)^n 匹，
となる，ということなので， 一番分かりやすく Δt = 1 として, 400秒後までにどうなるかを調べてみると，
In[1]:= a = Table[100* (1+0.009531*1)^n, {n, 0, 400}];
In[2]:= ListPlot[a]
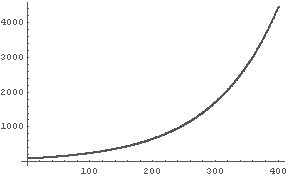← んん〜，どこかで見たような(^-^)
というグラフが得られる．
この調子だと，最初の数はわずかでも，爆発的にバクテリアが増えていくことがよくわかる．
□ レポート課題 1
上では Δt = 1 としたが，Δt は小さければ小さいほど理論上はよい近似のはずである．
そこで，Δt = 0.5 とした場合，
0.2 とした場合，
0.1 とした場合，
について各々同様に 0〜400秒程度まで値を求め，グラフを描いてみよ．
→ もとの近似もそう悪くないので，ほぼ同じ形状になってしまうだろうが，まあやってみるべし．
→ 「理論上はよい近似」というのは，本当は計算の過程で丸め誤差と呼ばれる誤差が混入してくるため，計算回数が多いとかえって不利になるからである．
詳しくは数値計算の議論になるが…
□ レポート課題 2
上のグラフは，第5回の授業で
「1割/10日 の複利で 100万円借りたとして借金総額がどうなるかを 400日までグラフにした」
ものとそっくりである．
これはなぜか，を説明せよ．
さて，今回は漸化式の答えがなんとなくわかってしまっている．つまり，
nΔt秒後には un = 100 * (1+0.009531Δt)^n
ということで，un がわかっている．
そこでこの極限を用いて，本来の微分方程式の厳密解 u(t) を推定してみよう．
まず，どう極限をとったらよいか考えるために，たくさんある変数の関係を整理しよう．
時間 t と漸化式の添字 n と微少時間 Δt の関係は
t = nΔt
である． 束縛する式が 1つある，ということは，この(3つの)変数のうち， 一つは独立でない，つまり消去されるべき変数だ，ということである． で，最終的に欲しい答えは u(t)であるから，本来の主役は時間 t であって，と考えると n か Δt のどちらかは
n = t/Δt,
Δt = t/n
のどちらかの関係式を用いて消去されるべき変数であることがわかる． で，最初に導入したのは Δt であり，n は t=nΔt より後から導入されたという順序を考えると n を消去するのが筋だろう． そこで，n を消去して漸化式の厳密解を書き直してみると，
t 秒後には ut/Δt = 100 * (1+0.009531Δt)^(t/Δt)
となり，これをわかりやすく整理すると，微分方程式の厳密解 u(t) との関係は
t 秒後には u(t) ≒ 100 * {(1+0.009531Δt)^(1/Δt)}^t
と書ける，と期待できる． で，Δt が無限にゼロに近くなれば微分方程式の厳密解に無限に近づく，と期待すると，
t 秒後には u(t) = lim 100 * {(1+0.009531Δt)^(1/Δt)}^t
Δt→ 0
= 100 * { lim (1+0.009531Δt)^(1/Δt) }^t
Δt→ 0
となることが「期待できる」．
→ あくまで「期待」である．
そうなるとは限らないので，厳密には数学的に証明等を通じて調べる必要がある．
さて，上の式を Mathematica を用いて計算してみよう．
● 極限値を求める … Limit[式, 変数 -> 変数の極限]
→ 変数が変数の極限に近づく際の式の極限値を返す．
→ ちなみに，無限大は Mathematica では Infinity と書かれる．
上の Limit というコマンドを用いて極限値を計算すると，
In[1] := Limit[ (1 + a*d)^(1/d), d -> 0]
← a = 0.009531 を具体的にいれてしまうと，数字で答えが返ってきてしまう．
今回はどういう関数になるかを見たいので，あくまで a のママで…
Out[1]= Ea ← E は自然対数の底. 約 2.71828... である．
となるので，これによって，微分方程式の解が
u(t) = 100 * (E0.009531)t
= u(0) * E0.009531*t ← 100 は考えてみれば u(0)である．
ではないか，と推測できる．
つまり，「離散近似と極限を用いて，微分方程式の解が推測できた」のである．
この結果をきちんと数学の仮説として書くと，
■ 仮説 1
常微分方程式 du/dt = a u の厳密解は u(t) = u(0) * Ea*t である．
(ただし， a は実数)
推定した微分方程式の厳密解のグラフと，先の漸化式から得たグラフとを重ねて描いて比べてみよ．
→ 授業中の課題
□ レポート課題 3
仮説 1 を数学的に証明せよ．
厳密な証明ができなくとも，自分なりに確認できるところまででもよい．
□ レポート課題 4
上とは違って，微分を
u(t) - u(t-Δt)
du/dt ≒ -----------------
Δt
と近似すると，微分方程式自体は
u(t) - u(t-Δt) 1
----------------- = 0.009531 u(t) ⇔ un+1 = --------------- un
Δt 1 - 0.009531Δt
と近似される．この場合についても Δt = 1 の場合だけでよいので同様に考察せよ． また，漸化式の解の極限を用いて微分方程式の厳密解を上同様に推定せよ．
さて，先ほどは単純にどんどん増殖できる，というモデルを考えたが，
これではあまりに単純すぎて, 数が一方的に増えるだけであった．
しかし実際には，増えすぎれば食糧が足りなくなったり病気が蔓延したり
して，増殖が抑えられる，というのが現実だろう．
そこで，先ほどは無視したこうした効果を考慮にいれ，モデリングしてみよう．
このために一番簡単な方法は，ある数 umax を越えると食糧
が足りない，病気が蔓延する，等の理由でかえって不利だ と考えて，
の二つのファクターを考慮して，次のような微分方程式(ロジスティック方程式)を考えることだろう．
du/dt = r * u * (-1)(u - umax) , r > 0
適当に個数の単位を変換すれば umax = 1 と書き換えられるので，そうしておこう． すると，ロジスティック方程式は次のようになる．
(ロジスティック方程式) du/dt = r u (1 - u), r > 0
さて，ここでもこの微分方程式を今まで同様の方法で考察してみよう． まず例によって離散近似を行ってみると，
u(t+Δt) - u(t) 1+rΔt
----------------- = r u(t) (1-u(t)) ⇔ un+1 = rΔt un (------- - un)
Δt rΔt
となる． ただし，上と同様に t = nΔt, un := u(nΔt) である． このままだと扱いにくいので，
rΔt R
vn := ------- un, R := 1+rΔt ⇔ un = ----- vn
1+rΔt R-1
と大きさあわせをしておくと，漸化式は
(ロジスティック写像) vn+1 = R vn (1-vn)
と単純になるので，これをもとにいろいろ調べてみよう．
ちなみに，v と u の関係をきちんと図式しておくと，
umax R
‖ ----- → ∞ (Δt→0 の時)
0 1 R-1
----+---------------+---------------+-------------------------> u (真の値)
| | |
? | まだ増えられる | もう多過ぎる | ? ← 想定している状態
| | |
----+---------------+---------------+-------------------------> v (便宜上の値)
0 R-1 1
-----
R
となるので，「バクテリアの増減」を考えていて混乱したときはこの図式を思い出すこと．
さて，さっきのように単純な場合は，un の具体的な形が推測できたので
Table でいきなり答えをリストアップできたが，今度はそうはいかなさそうだ．
そこで，一つずつ真面目に v0 → v1 → v2 → v3 → …
と計算していくしかあるまい．
それでも何かわかるだろうか．
まずは Mathematica でロジスティック写像そのものを Logistic[R, v] と定義して，
それを利用して計算を重ねてリストにしていく関数を LAddlist[R, リスト] として作ってみる．
In[1]:= Logistic[R_, v_] := R * v * (1 - v) // N[#, 150] &
← どうしてもかなりの有効桁数が必要となる(初期値敏感性のため)．
In[2]:= LAddList[R_, list_] := Append[list, Logistic[R, list[[-1]] ] ]
← リストの最後の要素のロジスティック写像を計算して，つけくわえている．
これなら，一回の計算で一つ要素が増える．
ただし，途中で
● リスト の最後に要素を加える … Append[リスト, 要素]
→ Append[{1,2,3}, x] は {1,2,3,x} となる．
→ 本当はもっと早く計算できる方法があるが，扱いが面倒なので略．
知りたいものは，Append のヘルプを読むとよい．
を用いている．
こうすると，例えば，R=2, v0 = 0.2 としたロジスティック写像を考えると，
In[3]:= Logistic[2, 0.2] ← 1回目の写像を確認．
Out[3]= 0.32
In[4]:= LAddList[2, {0.2}] ← ロジスティック写像を行うと，
Out[4]= {0.2, 0.32} ← 計算された分がリストの最後に加わる．
In[5]:= LAddList[2, %] ← 得られた結果にさらに計算を行うと
Out[5]= {0.2, 0.32, 0.4352} ← さらに増える．
となるので，Nest を上手に使って，v0, v1, v2, ..., vn は次のように求められる．
In[6]:= Nest[LAddList[2, #]&, {0.2}, 100]; ← R=2, v0 = 0.2 として,
v0, ..., v100 を求めている．
In[7]:= ListPlot[%6, PlotJoined -> True, PlotRange -> {0,1}]
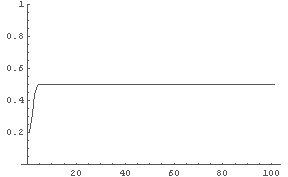← v = 0.5 に収束しているようだ
グラフを見ると，v = 0.5 に収束しているようだ．
つまり，vn の具体的な形はわからないが，
vn → 0.5 (n→∞)
が推測できる，ということである．
さて，上の初期値にたいしては v が収束したが，初期値を変えてみたら挙動はどうなるだろうか．
これは，バクテリアが最初に何匹いたか，を変えてみることに相当する．
面倒なので，一度にグラフを出力してみると，
→ ● 軸の交差する位置を決める … オプション AxesOrigin
を用いて，
In[8]:= Table[
ListPlot[
Nest[LAddList[2, #] &, {0.1*n}, 10], ← v0= 0.1 * n = 0.1 〜 0.9 としている
また，せいぜい 10点で収束するだろう，とみなしている．
PlotJoined -> True,
PlotRange -> {0, 1},
AxesOrigin -> {0, 0} ← 原点で軸が交差するようにというオプション
],
{n, 1, 9} ← v0= 0.1 * n = 0.1 〜 0.9 としている
];
Out[8]= …略…
In[9]:= Show[%] ← 上で出力した複数のグラフを一度に重ねてみると，
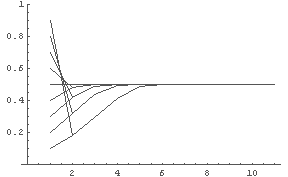← どれも v = 0.5 に収束しているようだ
この図から，初期値を変えてみても R=2 の時は v=0.5 (すなわち u=1)
に収束するようである．
よって，次のような仮説がたてられる．
■ 仮説 2
R=2 のロジスティック写像を繰り返し作用させると，初期値によらず
v=0.5 に収束する．
→ 実は，初期値 v0 を v0 < 0 や v0 > 1
とするとそうはいかない．
つまり，この仮説には間違いがある．
よって，より正確にはどうしたらよいか? → 課題
□ レポート課題 5
仮説 2 が成立する初期値は実は範囲が限られている．
その範囲を求め，仮説 2 を正しいと思われる形に修正せよ．
また，その範囲の外ではなぜ仮説 2 が成り立たないか説明せよ．
さて，R=2 の時は(ある範囲の初期値にたいして) v は収束した．
よって，微分方程式の解 u もある値に収束することが予想できる．
それを確かめてみよう．
それには，先ほどと同様に，Δt → 0 の極限をみてみるのがよいだろう．
ロジスティック方程式とロジスティック写像との変数の関係を眺めてみると，
Δt → 0 ⇔ R → 1 (上から)
という関係にあるので，R を 1 に近づけつつ，ロジスティック写像の収束先を調べてみれば良さそうだ． つまり，
lim ロジスティック写像の収束の挙動 = lim ロジスティック写像の収束の挙動 = ロジスティック方程式の収束の挙動
R→1 Δt→0
と期待する，ということである． まず，与えられた R に対して v の収束値を求める関数 Converge[R] を作ってみよう．
In[10]:= Converge[R_] :=
Table[
Take[Nest[LAddList[R, #] &, {0.05*n}, 300] -3], ← 念の為に 300 まで計算させたうえ，
収束したかどうか見るために最後の3つをとる．
{n, 1, 19} ← 19 個の初期値に対して計算している．
] // Flatten // Rationalize // Union ← 得られた値の重複を取り除く．
In[11]:= Converge[2] ← ためしに R=2 を計算してみると
Out[11]= {1/2} ← 1/2 「だけ」が求まって，収束したこととその値がわかる．
とすればよい．ただし，途中で
● ネストした(=多重になった)リストをフラットにする … Flatten[リスト]
→ Flatten[{{a,b},{c},{d,{e}}}] は {a,b,c,d,e} となる．
→ さらに，Flatten[リスト, 数] とすると，指定した数の深さのネストをフラットにする.
例えば，Flatten[{{a,b},{c},{d,{e}}},1] は {a,b,c,d,{e}} となる．
● 近い有理数で置き換える … Rationalize[実数]
→ 決められた誤差よりも近い有理数がある場合のみ，置き換えられる．
→ 非常に小さい誤差分だけ違う数値を同じと見なすのに便利に使える．
● 重複する除いて要素をリストアップ … Union[リスト]
→ Union[{a,b,b,b,c,d,d}] は {a,b,c,d} となる．
を用いている．
さて，この関数 Converge[R] を用いて，R を変えてみると，
In[12]:= Table[Converge[1+0.1*n], {n, 1, 10}]
← R = 1.1, 1.2, .. 1.9, 2.0 の場合について v の収束値を計算．
Out[12]= {{1/11}, {1/6}, {3/13}, {2/7}, {1/3}, {3/8}, {7/17}, {4/9}, {9/19}, {1/2}}
となる．
よって，R = 1.1, 1.2, .. 1.9, 2.0
のどの場合についてもロジスティック写像は 0 < 初期値 < 1 とすると一定の値に収束することがわかる．
さらに，収束した値について調べてみよう．
Out[12] の値は v∞ の値だから，u∞ に直すには各々 R/(R-1) をかければよい．
In[13]:= Table[Converge[1+0.1*n] * (1+1/(0.1*n)), {n, 1, 10}]
← R = 1.1, 1.2, .. 1.9, 2.0 の場合について u の収束値を計算．
Out[13]= {{1.}, {1.}, {1.}, {1.}, {1.}, {1.}, {1.}, {1.}, {1.}, {1.}}
← 全て 1 になった．
これはどういうことかというと，
lim u∞ = lim u∞ = 1 (= umax)
R→1 Δt→0
ということである(そのまんま)．
よってこれをきちんと仮説として書くと，初期値についてもきちんと考えて，
■ 仮説 3
ロジスティック方程式(微分方程式)の解は初期値が 0 より大きければ
umax = 1 に収束する．
ということになる．
これは言い換えれば，
「ロジスティック方程式にしたがって増減するバクテリアは，最終的に umax 匹になる」
と予想できたということである．
→ ここでも
「離散近似と極限を用いて微分方程式の厳密解について知見を得られた」
ことに注意せよ．
□ レポート課題 6
仮説 3 が初期値 ≦ 0 で成り立たない理由を自分なりに説明せよ．
□ レポート課題 7
仮説 3 を数学的に証明せよ(← 無理しなくてよいが…)．