↑ かなりすごいことになっている
さて,今回は Mathematica を普通に使うために必要な
「プログラミング」と
「グラフ描画」
についてごく簡単に学ぶ.
プログラミングというと難しく聞こえるが,
「具体的にはどうやって計算するか」をコンピュータに
「具体的に教える」だけの話である.
計算したいものが同じでも具体的な計算方法は異なっても良いことから,
プログラムも個人によって異なるのは当然であり,
そこに「上手,下手」が現れてくる.
プログラミングに習熟することは「思考過程を言語化」することに慣れるという側面もあるので,
早くから慣れておくのが良い.
グラフについては,gnuplot に既に学習したので不要に思うかも知れないが,
対話計算を主とする Mathematica などでは結果を「その場で目でみる」ことが重要であり,
習熟不足のためにグラフ化が面倒になるようでは Mathematica を使えるとは言えない.
Mathematica ではちょっとややこしい計算は名前をつけて関数にしてしまい,
それを単位として扱うのが全体を見通し良くするコツの一つである.
それには自分の思考,計算過程をいかにコンピュータの言語で表すかという技術が必要になる.
ここでは,ごく簡単に計算の方法を Mathematica で表す方法について述べる.
なお,ごく簡単な関数をどうやって定義するかについては前回の授業の
簡単な関数の定義
を参照すること.
まずは条件分岐について触れておこう. 一般に条件分岐は「もし A ならば処理 1 を,B ならば 処理 2 を」というように条件によって動作を変えるのに使われる. これによって,プログラムの動作を制御することができるという意味で初歩の初歩の技術であるので,しっかり学習するように.
まずは一つだけの条件で,その条件も yes か no という答えしか返さない
一番簡単な例について学習しよう.
例えば,BMI(Body Mass Index): 体重(kg) / (身長(m)^2) を見て太り過ぎかどうかの判定をする関数を考えてみよう.
(日本肥満学会では BMI が 25以上で肥満とする)
例
In[1]:= BMI[w_, h_] := w/(h^2) ← w:体重(kg), h:身長(m)
In[2]:= BMI[64, 1.68]
Out[2]= 22.6757
In[3]:= himan[x_] := If[ 25 <= x,
Print["BMI=",x, " is HIMAN"],
Print["BMI=",x, " is not himan"]
]
In[4]:= himan[BMI[64, 1.68]]
Out[4]= BMI=22.6757 is not himan
In[5]:= himan[BMI[75, 1.68]]
Out[5]= BMI=26.5731 is HIMAN
ただし,途中で
表示 … Print[表示したいもの(カンマで区切って並べる)]
というコマンドを用いている.
注意
Print コマンドは「画面に出力はする」が,「関数の値にはならない」.
つまり,Print コマンドを使った出力は他の関数の入力に使うための再利用が難しい.
よって,Print コマンドはあくまで人間の「確認用」に使うだけにして,
関数の結果出力に直接使わないようにしよう.
そういう意味で,この himan 関数はあまり良くない書き方になっている.
改善方法については,後述の Himando 関数のところで述べているのでそこを見よ.
評価式n を順に比較して,最初に True (真)になる最初の n に対して 式n を実行する.
(次の Switch と似たような動作をするので,そちらもみておくこと)
このコマンドを用いる例を考えてみよう.
例えば,日本肥満学会では BMI に応じて
| BMI | < 18.5 | 18.5≦ | 25≦ | 30≦ | 35≦ | 40≦ |
|---|---|---|---|---|---|---|
| 分類 | 低体重 | 普通 | 肥満(1度) | 肥満(2度) | 肥満(3度) | 肥満(4度) |
と肥満症を分類しているので,この分類を行う関数を作ってみよう.
例
In[1]:= Himando[x_] := Which[
x < 18.5, Print["yase"],
x < 25, Print["futsuu"],
x < 30, Print["himan 1"],
x < 35, Print["himan 2"],
x < 40, Print["himan 3"],
True, Print["himan 4"] ← ここまで来たら必ず成り立つよう書かれている.True というのは常に「真」となる特別な式であると思えば良い.
]
In[2]:= Himando[BMI[65,1.68]]
Out[2]= futsuu
In[3]:= Himando[BMI[120,1.68]]
Out[3]= himan 4
注意
さて,上の Himando 関数を他の関数から再利用したい,ということを考えると,
先にも述べた理由によって Print コマンドは使わない方がよい.
つまり,Print 命令は「画面に出力はする」が,「関数 Himando の値にはならない」からである.
そう考えて改良すると,例えば次のように「関数 Himando の値として数字や文字列を返す」などとするのがよい.
In[4]:= Himando[x_] := Which[
x < 18.5, -1,
x < 25, 0,
x < 30, 1,
x < 35, 2,
x < 40, 3,
True, 4
]
In[5]:= Himando[BMI[65,1.68]]
Out[5]= 0 ← かえって分かりにくくなったような気が最初はするが…
こうすると,Himando を他の関数から簡単に利用できる. Module の説明の部分で Advice という関数を作ってその例を示すのでみておくと良い.
評価式と評価n を順に比較して,評価式が評価n にマッチする最初の n に対して 式n を実行.
先の Which 命令と似ているが,より問題がシンプルなケースに使える.
さて,関数の内部でやや複雑な計算が必要となるような場合にどうやって関数を定義して用いるのか,
について学習しよう.
なお,複雑な関数をどうやって定義するかについては前回の授業の
複雑な関数の定義 … Module
を参照すること.
さてここで,先の修正した Himando 関数がどう「再利用されるか」の例を作成してみよう. これをみれば「関数の再利用」がどういうのものか,そして,その便利性がよく分かるはずである.
例
In[6]:= Advice[x_] := Module[{h, alist, r},
alist = {
"yasesugi desu. motto tabemasyo",
"futsuu desu. konomama ikimasyou",
"himando 1 desune. sukosi yasemasyou",
"himando 2 desu. kanari yabaidesu. yasero.",
"himando 3 da. yabai. yaseroyo.",
"himando 4. futorisugi. iikagen yasero."
};
h = Himando[x];
r = alist[[h+2]]; ← リストは常に「1番」から始まるので +2 として合わせておく.
Return[r]
]
In[7]:= Advice[BMI[75, 1.68]]
Out[7]= himando 1 desune. sukosi yasemasyou
注意 こうすることで,「肥満度の判定」と「アドバイス」を分離できるということが重要なのである. つまり,肥満度の判定の基準が多少変わっても Himando 関数を変更するだけでよく, Advice 関数は変更しないで済む.
コンピュータに計算をさせる基本的なテクニックに「反復」がある.
この反復が理解できないと,手で計算するのと機械に計算させるのとで手間
が変わらないことになりかねないので,まずは理解できるように努力しよう.
まずは次に示す基本的な,通常のコンピュータ言語にも必ず実装されている
と言って良いコマンドから習熟すると良い.
ただし,後でも示すように,Mathematica にはこれら基本コマンドよりも便利なコマンドが多くあり,
かつ,それらを使った方が計算が早かったりするので,
基本コマンドだけで済ませようと思わない方が良い.
step_i おきに i を min_i から max_i まで変えながら式を繰り返す.
まずはこの簡単な Do や次の For, While などを理解してから次へ進むのが良いだろう.
例えば,月の利息が 1% の借金をして,12ヶ月たつといくらになるか? を計算する関数をつくると,
次のようになる.
例
In[1]:= Debt1[x_] := Module[{y},
y = x;
Do[y = y*1.01, {i, 1, 12}]; ← y に新しい y を代入して更新している.
Return[y]
]
注意 上の例にもある「代入による変数の値の更新」は, コンピュータを用いた計算の基本テクニックなのでよく慣れておくこと.
初期条件を評価した後に,ループに入る.
各ループでは,ループ条件が満たされれば式1,式2 の順序で評価され,もう一度ループに入る.
ループ条件が満たされない場合,ループ終り.
Continue コマンドとの整合性のためにこのような仕様になってい
るが分かりにくい(^-^).
ちなみに,Continue コマンドは使わない方が良い代表的なコマンドである.
よって紹介しない.
例えば,月の利息が 1% の借金をして,12ヶ月たつといくらになるか? を計算する関数をつくると, 次のようになる.
例
In[2]:= Debt2[x_] := Module[{y},
y = x;
For[i = 1, i <= 12, i++, y = y*1.01];
Return[y]
]
注意 i++ は(値を 1増やして元の値を返す)の省略形である. 他にも++i, i--, --i, i+=a, i-=a, i*=a, i/=a などの省略した形式がある. これらの意味を Help で調べてみよ.
条件が真ならば式を評価し,また条件をチェック,を繰り返す.
条件が偽になったら終り.
例えば,月の利息が 1% の借金をして,12ヶ月たつといくらになるか? を計算する関数をつくると,
次のようになる.
例
In[3]:= Debt3[x_] := Module[{y, i},
y = x;
i = 1;
While[i <= 12, y = y*1.01; i++]; ← y=..;i++ は大きな一つの式と見なされている
Return[y]
]
Mathematica には上に示した基本的な反復コマンドよりも便利なコマンドがある.
それが
高階関数 … (Mathematica では)関数を引数にとる関数のこと
である.
これは数式処理ソフト特有のコマンド群であり,
使いこなせると上の反復の基本コマンドを使うよりも便利なことが多い.
Mathematica を使いこなそうと思うレベルになったらまずはこれらのコマンドに習熟すべきである.
Map で明示しなくても良いケースも多い.
例
In[1]:= a = {1,2,3,4}
In[2]:= Map[Sin, a]
Out[2]= {Sin[1],Sin[2],Sin[3],Sin[4]}
In[3]:= a // Sin
Out[3]= {Sin[1],Sin[2],Sin[3],Sin[4]}
In[4]:= Sin[a]
Out[4]= {Sin[1],Sin[2],Sin[3],Sin[4]}
In[5]:= % // N
Out[5]= {0.841471, 0.909297, 0.14112, -0.756802}
レベル指定を {1} として,リストの中身を書き換えるのに便利.
例
In[1]:= a = Table[Sin[n], {n,4}]
Out[1]:= {Sin[1], Sin[2], Sin[3] , Sin[4]}
In[2]:= Apply[Cos, a, {1}]
Out[2]= {Cos[1], Cos[2], Cos[3], Cos[4]}
In[3]:= Apply[Plus, a]
Out[3]= Sin[1]+Sin[2]+Sin[3]+Sin[4]
← レベル指定しないと,{0},すなわち最初の頭部と見なされる.
a は正確には List[Sin[1],Sin[2],Sin[3],Sin[4]] のことであるので,
これは Plus[Sin[1],Sin[2],Sin[3],Sin[4]] = ... と置き換えられる.
条件関数をリストの要素に適用して,True となるものだけを取り出す.
例
In[1]:= a = {1.0, -3, 5, 4, 3.5, -1.2}
In[2]:= Select[a, Positive]
Out[2]= {1.,5,4,3.5}
例えば,Nest[f, x, 5] は f[f[f[f[f[x]]]]] を意味する.
とても便利なコマンドなので是非とも使えるようになっておきたい.
月の利息が 3% の預金をするとして,100万円を預けると 2年後には複利で幾らになるか…
例
In[1]:= Debt[x_] := x * 1.03
In[2]:= Nest[Debt, 100, 24]
Out[2]= 203.279
Nest に似ているが,関数の第二引数がリストの要素になる.
例えば,Fold[f, x, {2,1,5}] は f[f[f[x, 2], 1], 5] を意味する.
例えば,((1.32)0.7)1.2 を計算するには…
例
In[1]:= Fold[Power, 1.3, {2, 0.7, 1.2}]
Out[1]= 1.55391
こうしたツールでグラフを描くというと,
「データをプロットする」という場合と,
「数式を描く」という場合がある.
データをプロットする方法は前回
リストをグラフで見る
で学習したので,そちらを参考にすると良い.
より詳しくは Help をみるのが良いだろう.
複数のグラフを同時にに描くには, Plot[{関数1, 関数2, ... }, 変数の範囲] とする.
10日借りると 1割の利息が複利でつく借金をしたとして,
x 日後に借金はいくらになっているか,関数を作ってグラフ化してみよう.
例
In[1]:= Pay[x_, gankin_] := gankin * (1.1^(x/10)) ← 元金を gankin としての x 日後の借金総額
In[2]:= Table[{n, Pay[n, 100]}, {n, 0, 100, 10}] // TableForm
Out[2]//TableForm= ← 100(万円)借りたとして借金がどうなるか10日毎に100日までの様子の確認.
0 100
10 110.
20 121.
30 133.1
40 146.41
50 161.051
60 177.156
70 194.872
80 214.359
90 235.795
100 259.374
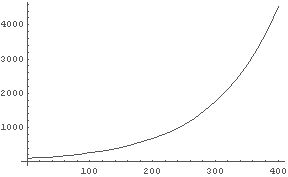
In[3]:= Plot[Pay[x,100], {x,0,400}] ← 100(万円)借りたとして400日までの様子をグラフ化.

↑ かなりすごいことになっている
注意 これはグラフの両軸が「そのまま」であるが,片方,もしくは両方の軸を対数表示する 「対数グラフ」も Mathematica では簡単に書ける. それには, LogLinearPlot や LogLogPlot などのコマンドを使えば良い. 詳しくは Help で調べるか,先週示した参照文献を調べると良いだろう.
グラフをファイルとして出力する
Mathematica で得られたグラフをファイルに出力したい,というときは,
そのグラフを右クリック
→
編集
→
選択範囲の形式保存
→
EPS
としていったん eps ファイルにグラフを保存する.
その後,
Postscript ファイルから他の画像ファイルへの変換
を参照しながら png ファイルなどに変換してから web に掲載すればよい.
以下に示す課題について
能う限り賢明な調査と考察を行い,
InformationLiteracy-04
という題名をつけて e-mail にて教官宛にレポートとして提出せよ(教官のメールアドレスは授業中に口頭で伝える).
なお,レポートを e-mail の代わりに TeX で作成した書面にて提出してもよい.
注意
なお,本レポートは単位認定のための必須要件「ではない」.
ただし,提出することにより成績に加点されるので,単位があやしい,
成績が気になるという者は積極的に提出する方がよいだろう.
f(n) = n/2 : n が偶数の場合 f(n) = 3n+1 : n が奇数の場合を考える.