

最終更新日 …
$Date: 2004-06-21 15:26:13+09 $


さて,今回からは Mathematica について学ぶ.
Mathematica とは数式処理ソフトとよばれるソフトウェアの代表的なものである.
その機能は基本的に「入力した数式を,利用者の要求に応じて変形する」というものである.
ただそれだけかと思うかも知れないが,
われわれ人間が数学で何か処理を行う時の作業時間の多くが数式の変形にかかることを考えると,
コンピュータの正確さと高速性を利用できるこの種のソフトウェアのインパクトが理解できよう.
この種のソフトウェアは,
上手に使えば,
これまで紙と鉛筆だけでは得られなかった数学的知見を得ることを可能にするものである.
数学科の学生としては Mathematica などのソフトウェアを使いこなすことは長い目でみてやはり必須の能力となるだろう.
Mathematica
は非常に巨大で複雑なシステムをなすソフトウェアであり,
使いこなすにはなにか適切な参考文献の助けが必要であるだろう.
幸い,Mathematica に関する書籍は数多く出版されているので,
書店で自らに合うものを選択するのも良いだろう.
また,以前学習した「web を用いた図書の検索」を利用して大学の図書を上手に活用するのもよい.
しかし,Mathematica に関する web や書籍はあまりに数多く,どれを選んだら良いのか初学者としては迷うだろう.
そこで,Mathematica に関する web と参考文献を絞りこんで紹介する.
mathematica & と入力.
書式 >> スタイルシート を選んで,Default 以外に変更するとだいぶ見た目が変わってくる.
好みのものを選ぶと良い.
いつもそのスタイルを使いたいのであれば,
編集 >> 環境設定 >> Global Options >> File Locations >> DefaultStyleDefinition
を変えれば良い.
# スタイルの定義ファイルは
/usr/local/mathematica/SystemFiles/FrontEnd/StyleSheets
に置かれている.
Mathematica では入力はコマンド列をキーボードで入力後,
Shiftキー と Return(Enter)キーを同時押し
というシステムになっている.
注意
忘れがちなので注意すること.
Help は Mathmatica 画面右上の「Help」をクリックするか,Mathematica
上で
"?調べたいもの"
と入力する.
また,オプションや関数の属性まで調べたいという時は
"??調べたいもの"
と ? を重ねればよい.
Options[調べたいもの] でもオプションは調べられるが,??
の方が楽だろう.
調べたいものの文字中に不明な部分があれば * (アスタリスク)で代用できる.
この時は該当しそうなものを Mathematica がリストアップしてくれる.
Mathematica をどれくらい使えるかは,Help を使いこなせるかどうかが鍵になる.
とにかく Help をばりばり使ってみるのが良い.
例
In[1]:= ?Si*
System`
Sign Sin Sinh
Signature SingleLetterItalics SinhIntegral
SignPadding SingularityDepth SinIntegral
Simplify SingularValues SixJSymbol
In[2]:= ?N
N[expr]は,式exprの値を数値で与える.
N[expr,n]は,可能であれば n 桁精度で結果を与える.詳細
Mathematica でつかえる括弧は 3種類(厳密には 4種類)あり,それぞれ役目が違う. 普通にわれわれが手書きするときと違うので,注意が必要.
Mathematica では入力時にこれまでの出力を参照,再利用できる. % で一番新しい出力結果が,%% で一つ前の結果が,%%%%...(k回) で k個前の出力結果が参照される. また,%n もしくは Out[n] で(最初から数えて) n 番目の出力結果を参照できる.
例
In[1]:= 2^3
Out[1]= 8
In[2]:= 4*3
Out[2]= 12
In[3]:= % + %%
Out[3]= 20
In[4]:= Out[1] * %
Out[4]= 160
数式処理を基本とする Mathematica であるが,
値を「数値で」扱うこともできる.
それには,N[式, 桁数] とすればよい.
例
In[1]:= N[1/7, 100]
Out[1]= 0.1428571428571428571428571428571428571428571428571428571428571428571428571428
571428571428571428571429
変数をつくってそこへ数式を代入することができる.
この機能を使うことで Mathematica を便利に使えるようになるので,
なるべく代入を頻繁に使うように心掛けよう.
注意
使わなくなった変数や関数は
Remove[ ]
コマンドで「リセット」できる(使わなかった状態に戻る).
変数を使いすぎて分からなくなったときなどは Remove でなるべく素の状態にして計算しよう.
Mathematica で利用できる(数学)定数や関数は非常に多い.
そのうちの基本的なものの一部を挙げておく.
詳細はマニュアルを参照せよ.
注意
実は,Mathematica には関数の記法が何種類かある.
後学のために,以下に記しておく.
f[x]
のように,関数名[引数名] という記法である.
曖昧さがなく確実だが,カッコが多くなると煩わしい.
f@x
のように,関数名@引数名 という記法である.
簡潔だが, どこまでが引数なのか曖昧なので使わないことを勧める.
{1,2,3,5}~Union~{2,4,6}
のように,引数1 ~関数名~ 引数2 とする記法である.
こうすると分かりやすくかけることがある.
x // f
のように,引数名 // 関数名 という記法である.
慣れると分かりやすい.
これらの記号で式を比較することができる.
===, =!= は各々 ==, != の「厳密バージョン」.
左右の式そのものを厳密に比較することになる.
普段は使わなくてよいだろう.
注意
=(イコール) 一つだけでは等価性判定にならない(代入になる)ことに注意.
例
In[1]:= 3 <= 5
Out[1]= True
In[2]:= 3 >= 5
Out[2]= False
In[3]:= 3 == 3.0 ← 3 と 3.0 は等しいか? という式
Out[3]= True
In[4]:= 3 == 5 ← 3 と 5 は等しいか? という式
Out[4]= False
In[5]:= 3 != 5 ← 3 と 5 は違うか? という式
Out[5]= True ← 確かに違うので True と答えが返ってくる.
In[6]:= 3 === 3.0 ← 3 と 3.0 は等しい「式」か?
Out[6]= False ← 式としては等しくないので False になる.
In[7]:= 3 =!= 3.0 ← 3 と 3.0 は違う「式」か?
Out[7]= True ← 確かに違うので True と答えが返ってくる.
数式処理を行うと,数式はどんどん複雑な表現になっていくのが普通である.
そこで,式を簡潔にしてわかりやすくしたいというときにこのコマンドを用いる.
なお,仮定が無い場合は省略できる.
また,仮定が複数ある場合は{ }で囲む.
注意
(不)等式の最も単純な形式は「正しいか否か」であるので,(不)等式の正否の判定に使える.
注意2
仮定の条件が不足な時は判定が保留され,(不)等式がそのまま表示される.
つまり,(不)等式が成立するための条件が不足しているかどうかを判定することもできる.
例
In[1]:= Simplify[Sqrt[x^2], x<0]
Out[1]= -x
In[2]:= Simplify[1/a < 1/b, 0 < b < a]
Out[2]= True
In[3]:= Simplify[1/a < 1/b, b < a]
Out[3]= 1/a < 1/b
In[4]:= Simplify[3 == 5]
Out[4]= False
In[5]:= Simplify[a+b > 2*(a*b)^(1/2)] ← 相加相乗平均に関する不等式を調べてみると…
Out[5]= a+b > 2*(a*b)^(1/2) ← 条件がどこかおかしいらしく,そのまま突き返される.
In[6]:= Simplify[a+b > 2*(a*b)^(1/2),{0<a, 0<b}] ← 条件を加えてみたが,
Out[6]= a+b > 2*(a*b)^(1/2) ← まだどこかおかしい.
In[7]:= Simplify[a+b >= 2*(a*b)^(1/2),{0<a, 0<b}] ← 等号もありえるな…
Out[7]= True ← Good!
実習
上で出てきた例を参照しながら,これまでの学習内容を理解すべく実習を行え.
Mathematica では何かを列挙したものはリストと呼ばれる形式で扱うのが便利である.
数列やベクトルのようなもの,と思えば良いだろう(数学的には全然そうした性質はないが).
リストを作成するには,
{ }
の中に要素を直接書き込むか,
Table[式, {コピーの数}] などとするのがよい.
詳しくはマニュアルを参照すべきであるが,次の例で大体分かるだろう.
例
In[1]:= {1,3,2,0}
Out[1]= {1, 3, 2, 0}
In[2]:= Table[1/n, {n,1,10}]
Out[2]= {1, 1/2, 1/3, 1/4, 1/5, 1/6, 1/7, 1/8, 1/9, 1/10}
二実数組からなるリストは,(x,y) 座標の組と見てグラフにすることができる.
例
In[1]:= a = Table[{n*2*Pi/50, Sin[n*2*Pi/50]}, {n, 50}]
Out[1]= …略…
In[2]:= ListPlot[a]
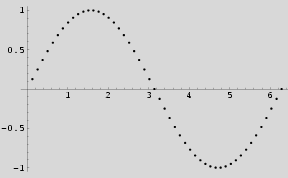
実習
上のように適当な数列を作り,ListPlot を行ってみよ.
また,そのグラフを画像として取り出して png ファイルに変形し,web に掲載してみよ.
(おまけ)Mathematica の画像のファイル出力
Mathematica でグラフを画像ファイルとして出力して利用するには次のようにすればよい.
二重大カッコ [[ ]] でリストの要素を指定できるのは上にも書いた通りである.
なお,
[[-1]] とすると最後の要素が出てくる.
例
In[1]:= a = {1, 4, 2, 8, 5, 7}
In[2]:= a[[-1]]
Out[2]= 7
In[3]:= a[[2]]
Out[3]= 4
例
In[1]:= a = {1, 4, 2, 8, 5, 7}
In[2]:= Length[a]
Out[2]= 6
こうするとリストを「人間に見やすく表示」することができる.
→ 実際に使うには,
リスト // TableForm
という入力方法が間違えにくくて良いだろう.
例
In[3]:= TableForm[Table[{n,N[1/n]},{n,10}] ]
Out[3]//TableForm=
1, 1.
2, 0.5
3, 0.3333333333333333
4, 0.25
5, 0.2
6, 0.16666666666666666
7, 0.14285714285714285
8, 0.125
9, 0.1111111111111111
10, 0.1
In[4]:= Table[{n,N[1/n]},{n,10}] // TableForm
Out[4]//TableForm=
1, 1.
2, 0.5
3, 0.3333333333333333
4, 0.25
5, 0.2
6, 0.16666666666666666
7, 0.14285714285714285
8, 0.125
9, 0.1111111111111111
10, 0.1
実習
循環小数 (おまけ)
上の方法で
1, 1/2, 1/3, ... を十分大きな数まで数値出力してみると,
■ 仮説 1/n が割り切れる ⇔ n = 2a5b
が成り立つように思われる.
…というのを実際にやってみて確認せよ.
また,この仮説が真に成り立つかどうか考えよ.
一次元のリストはベクトルとして, 二次元のリストは行列として見なすことができ, それに応じた線形計算が可能である.
MatrixForm
を用いる.
In[1]:= a={{1, 2},{3, 4}}
In[2]:= a // MatrixForm
Out[2]= (1 2)
(3 4)
リスト1 . リスト2
でベクトルの内積もしくは行列の積になる.
In[1]:= {a, b, c}.{x, y, z}
Out[1]= ax+by+cz
In[2]:= f={{a, b},{c, d}}
In[3]:= g={{x, y},{z, w}}
In[4]:= f.g // MatrixForm
Out[4]= (ax+bz ay+bw)
(cx+dz cy+dw)
Transpose
で転置行列を表せる.
In[1]:= a={{1, 2},{3, 4}}
In[2]:= a // MatrixForm
Out[2]= (1 2)
(3 4)
In[3]:= Transpose[a] // MatrixForm
Out[3]= (1 3)
(2 4)
LinearSolve[A, b]
とすると,
Ax = b
という連立一次方程式が解ける.
In[1]:= a={{1, 2},{3, 4}}
In[2]:= b={1, 4}
In[3]:= LinearSolve[a,b]
Out[3]= {2, -1/2}
Inverse
で,
(3次元ベクトル同志の)外積は
Cross
で,
行列の固有値,固有ベクトルは
Eigensystem
で,など,多数の便利な関数がある.
実習
上で出てきた例を参照しながら,これまでの学習内容を理解すべく実習を行え.
Mathematica で関数を定義する方法はいくつかあるが,もっとも簡単な方法がこの方法である.
まずはこの方法に習熟すべし.
注意
左辺の変数名のあとについている _ (アンダースコア) を忘れないように注意すること.
注意2
変数の部分でも記したが,
関数や変数の定義を消去するには,
Remove[関数名(or 変数名)]とする.
例
In[1]:= f[x_] := Sin[x]
In[2]:= f[Pi/2]
Out[2]= 1
Mathematica には「パターンマッチング」という概念がある.
関数の定義で左辺にこの概念が用いられている.
これは,「該当するものにマッチして,それを参照できる」というもので,
関数の定義を含め,さまざまな場面で必須のものである.
詳しくはともかく,簡単な使用例だけでもマスターしておくべし.
なお,
_ : 一つの式,__ :一つ以上並んだ式,___ :ゼロ個以上並んだ式
にそれぞれマッチする.
パターンには「ラベル」をつけられる.簡単な関数の定義で用いた x_ はその例で,
これがもっとも良く使われる使い方だろう.
例
In[1]:= repeat[{x__,y__,y__,z__}] := {y}
In[2]:= repeat[{0,1,1,1,3,5,1}]
Out[2]= {1}
In[3]:= repeat[{1,2,3,4,5,3,4,5,6}]
Out[3]= {3,4,5}
実習
反復作用(力学系, Newton 法)
正の実数 x に対する関数として
f(x) = x/2 + 1/x
を考える.
適当な正の実数 x に対して,f を何回も適用していくと
結果はどう変化するだろうか.
例
In[1]:= f[x_] := x/2 + 1/x
In[2]:= f[2] // N
Out[2]= 1.5
In[3]:= f[%] // N
Out[3]= 1.41667
In[4]:= f[%] // N
Out[4]= 1.41422
In[5]:= f[%] // N
Out[5]= 1.41421
この状況を良く考えて次の問いに答えよ.
注意
上のように「同じ関数を繰り返して適用する」場合に便利な命令として,
Nest,
NestList,
FixedPoint,
FixedPointList
などがある.
余裕があればこれらについても調べておくとよい.
さて,関数の内部でやや複雑な計算が必要となるような場合にどうやって関数を定義するか,
について学習しよう.
さて,そのためには次の Module コマンドを覚える必要がある.
| 文法 | 備考 |
|---|---|
関数名[変数名_] := Module[局所変数のリスト, 式; 式; ← 必要なだけ Return[式] ] |
局所変数→ Module[ ] の [ ] の中でだけ有効な変数
Return→ 関数の返り値. Return 文が無い場合,最後の式の値が返り値となる. なるべくなら Return 文を使うのが良い. というのも,最後の式の後ろに ;(セミコロン)をつけてしまうと さらにそのあとに「空の式」があると Mathematica は解釈するので, Return 文を使わない時 返り値がなくなる,と いう陥りやすい落とし穴があるからである(^-^;). (注) Mathematica では ; で区切られた式は「大きな一つの式」の扱いになる. |
例 例えば,20% の消費税を課した場合の値段を計算する関数を作ると,次のような感じになる.
In[1]:= f[x_] := Module[{tax},
tax = 0.2;
Return[x * (1.0 + tax)]
]
in[2]:= f[120]
out[2]= 144
実習
相加相乗平均
二つの正の実数に対して,
相加相乗平均を求め,
その二種類の平均に対してまた
相加相乗平均を求めるという計算を繰り返してみよう.
結果はどう変化するだろうか.
例
In[1]:= h[x_] := Module[{a,b},
a := (x[[1]]+x[[2]])/2;
b := (x[[1]] * x[[2]])^(1/2);
Return[{a,b}]
]
In[2]:= h[{1,2}]
Out[2]= {2/3, sqrt{2}}
In[3]:= h[%] // N
Out[3]= {1.45711,1.45648}
In[4]:= h[%] // N
Out[4]= {1.45679,1.45679}
この状況を良く考えて次の問いに答えよ.
さらに,上の計算にちょっと余計な計算を入れて次のような計算をしてみよう.
例
In[1]:= g[x_] := Module[{a,b,c,t},
a := (x[[1]]+x[[2]])/2;
b := (x[[1]] * x[[2]])^(1/2);
c := x[[3]] * 2;
t := x[[4]] - x[[3]] *(a-x[[1]])^2;
Return[{a,b,c,t}]
]
In[2]:= ini := {1, 2^(-1/2), 1, 1/4}
In[3]:= g[ini]
Out[3]= …略…
…以下 10回ほど g[%] を繰り返し…
In[12]:= N[ g[%], 20] ← ちょっと細かく出力させてみると…
Out[12]= {0.84721308479397908661,0.84721308479397908661,1024.0000000000000000,0.22847329052223181269}
In[13]:= q[x_] := (x[[1]]+x[[2]])^2 / (4*x[[4]]); ← こういう関数をつくって,
In[14]:= q[Out[12]] ← 上の結果を代入すると…
Out[14]= 3.1415926535897932385 ← どこかで見た数字が.
この状況を良く調べて次の問いに答えよ.