 �� ����=���֡��ļ�=��������������������ʵ�Υ(^-^)
�� ����=���֡��ļ�=��������������������ʵ�Υ(^-^)
����ϡ������व����������ˤĤ��Ƥޤ��ޤ��㤦���٤���Ĵ�٤Ƥߤ褦.
�ǡ����������Ǹ��������ߥ�졼�Ȥ��Ƥߤ��ߤ�ԤäƤߤ�.
����������ߤ���ʣ������̩�˹Ԥ��С�����ϼ��ѥ�٥�ˤ�ã����������������β����ǿ��ؤ丽�������ؤο������θ��������������.
�����ǤϿ��ʧ������Ļ�ε�ư��������Ѥ��ƥ��ߥ�졼�Ȥ��Ƥߤ褦.
�ޤ������ο��ʧ���Ϥ��ޤ�˿�äƤ��ޤä����ᡤ��ʬ�˰��⤷���ʤ�ʤ�.
�����⡤��������ˤ����ʤ�ʤ����֤��� �Ȥ����Ǥ⥷��ץ�ʾ���ͤ��褦.
# �Ĥޤꡤ�ּ��פβ�ǽ�������̤ꤷ���ʤ�.
�����ơ�����˥���ץ�ˡ����˹Ԥ���Ψ�� 1/2, ����˹Ԥ���Ψ�� 1/2 �����Ȥ��褦.
����ȡ�n ʬ��ˤϤ��ο��ʧ���ϥ���������������ɤ줯�餤Υ�줿���ˤ����������.
�ޤ��� Mathematica �ǻ�Ƥߤ褦.
In[1]:= Needs["Graphics`"]; �� ɬ�פˤʤ�Τǡ����ֺǽ��˺��ʤ��褦�ˤ�äƤ���.
In[2]:= Needs["Statistics`"]; �� �����ɬ�פˤʤ�.
In[3]:= Random[Integer] �� �Τ������ 0 �� 1 ����Ψ 1/2 �ǽФƤ���.
Out[3]= 1
In[4]:= Table[Random[Integer], {100}] �� ��� 100 ���äƤߤ�.
Out[4]= {1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0,
1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0,
1, 0, 0, 0, 0, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1,
0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 1, 1}
In[5]:= % /. 0 -> -1 �� �����عԤ� = +1�סָ���عԤ� = -1�פȤ��Ƥ����Ȥ��������Թ礬�ɤ������ʤΤǡ�
0 �� -1 ���ִ����Ƥ���.
Out[5]= {1, -1, -1, -1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1, 1, 1, 1, 1, -1, 1, 1, 1,
-1, -1, 1, -1, 1, 1, 1, -1, 1, -1, -1, -1, 1, -1, 1, 1, 1, 1, -1, 1, -1, 1,
-1, 1, -1, -1, 1, -1, 1, -1, -1, -1, -1, -1, 1, -1, 1, 1, 1, -1, -1, -1, -1,
1, -1, -1, -1, -1, 1, -1, -1, -1, 1, 1, -1, 1, -1, -1, 1, 1, -1, -1, 1, -1,
-1, -1, -1, 1, -1, -1, -1, 1, -1, -1, -1, 1, 1}
�� ���줬�ֿ��ʧ����100ʬ�δ֤����عԤä���������عԤä����Υꥹ��(^-^)��
In[6]:= FoldList[Plus, 0, %] �� �������� 0 �����Ƥ����ȡ�
Out[6]= {0, 1, 0, -1, -2, -1, 0, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9, 10, 11, 10, 11, 12,
13, 12, 11, 12, 11, 12, 13, 14, 13, 14, 13, 12, 11, 12, 11, 12, 13, 14, 15,
14, 15, 14, 15, 14, 15, 14, 13, 14, 13, 14, 13, 12, 11, 10, 9, 10, 9, 10, 11,
12, 11, 10, 9, 8, 9, 8, 7, 6, 5, 6, 5, 4, 3, 4, 5, 4, 5, 4, 3, 4, 5, 4, 3, 4,
3, 2, 1, 0, 1, 0, -1, -2, -1, -2, -3, -4, -3, -2}
In[7]:= Delete[ %, 1] �� ��η�̤κǽ�� 0 �ϰ�̣�ʤ��ΤǺ��.
Out[7]= {1, 0, -1, -2, -1, 0, 1, 2, 3, 4, 5, 4, 5, 6, 7, 8, 9, 10, 11, 10, 11, 12,
13, 12, 11, 12, 11, 12, 13, 14, 13, 14, 13, 12, 11, 12, 11, 12, 13, 14, 15,
14, 15, 14, 15, 14, 15, 14, 13, 14, 13, 14, 13, 12, 11, 10, 9, 10, 9, 10, 11,
12, 11, 10, 9, 8, 9, 8, 7, 6, 5, 6, 5, 4, 3, 4, 5, 4, 5, 4, 3, 4, 5, 4, 3, 4,
3, 2, 1, 0, 1, 0, -1, -2, -1, -2, -3, -4, -3, -2}
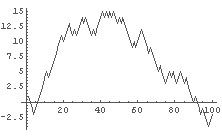
In[8]:= ListPlot[%, PlotJoined -> True]
 �� ����=���֡��ļ�=��������������������ʵ�Υ(^-^)
�� ����=���֡��ļ�=��������������������ʵ�Υ(^-^)
������������ǻȤä� Mathematica �ο������ؿ��ϡ��ʲ����̤�Ǥ���.
�� �Ѵ���§��Ŭ�� �� �� /. �Ѵ��롼��
�� �Ѵ��롼��ϡ�a �� b ���Ѵ��������Ȥ���a -> b �Ƚ�.
�� �㤨�С�x + y /. x -> 3 �Ȥ���ȡ������� 3 + y �ˤʤ�.
�� �ؿ�������˷����֤���Ŭ�Ѥ�����̤��¤٤� �� FoldList[�ؿ�, ����, �ꥹ��]
�� Nest �˻��Ƥ��뤬���ؿ�������������ꥹ�Ȥ����Ǥˤʤ롥
�� ư��Τ� Fold ��Ʊ�������������������ꥹ�ȤȤ��ƽ��Ϥ���������ۤʤ�.
Nest �� NestList �Ȥδط���Ʊ��.
�� �㤨�С�FoldList[f, x, {a, b, c}] ��
{x, f[x,a], f[f[x,a],b], f[f[f[x,a],b],c]}
�ˤʤ�.
�㤨�С�((1.32)0.7)1.2 �������ˤϰʲ��Τ褦�ˤ���.
In[1]:= FoldList[Power, 1.3, {2, 0.7, 1.2}]
Out[1]= {1.3, 1.69, 1.44385, 1.55391}
�� �ꥹ�� �����Ǥ��� �� Delete[�ꥹ�ȡ������ֹ�]
�� Delete[{a, b, c, d}, 3] �Ȥ���������� {a, b, d} �Ȥʤ�.
���ơ�����η����֤���������Ϥ���Τ����ݤʤΤǡ��̤�ƴؿ��ˤ��Ƥ��ޤ���.
���ʧ���������⤭���Τ�ΤΥꥹ�Ȥ���Ϥ���ؿ��� RW[�����],
���η�̤ˤ�äơ�n ���ܤǥ���������������ɤ줯�餤���ʤ��Ƥ��뤫�Υꥹ�Ȥ���Ϥ���ؿ��� RWpath[�����],
�Ĥ��Ǥˤ��η�̤�ץ��åȤ���ؿ��� RWplot[�����]
�Ȥ��ƺ�äƤߤ�.
In[9]:= RW[num_] := Table[Random[Integer], {num}] /. 0 -> -1
In[10]:= RW[100] �� ��˿��ʧ������� 100���⤫���Ƥߤ�.
Out[10]= {-1, 1, 1, 1, 1, -1, -1, 1, 1, 1, -1, 1, 1, 1, 1, 1, -1, -1, 1, -1, 1, 1, -1,
1, 1, 1, -1, 1, 1, 1, 1, -1, -1, 1, -1, -1, -1, 1, 1, 1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, 1, -1, 1, -1, -1, 1, 1, 1, -1, 1, 1, -1, -1, 1, -1, -1,
1, -1, -1, 1, -1, -1, 1, -1, 1, -1, -1, -1, -1, 1, -1, -1, 1, -1, 1, -1, -1,
-1, -1, 1, 1, 1, -1, -1, 1, -1, -1, -1, 1, -1}
In[11]:= RWpath[num_] := Delete[FoldList[Plus, 0, RW[num]] , 1]
In[12]:= RWpath[100] �� ��Ϥ�Ʊ�ͤ˻�Ƥߤ�.
Out[11]= ����
In[13]:= RWplot[num_] := ListPlot[RWpath[num], PlotJoined -> True]
In[14]:= RWplot[100] �� ��Ϥ�Ʊ�ͤ˻�Ƥߤ�.
Out[14]= ����
���ơ�����ǿ��ʧ������ˤ�����Ǥ��⤫���ơ����β�����դǸ���
���Ȥ���ñ�ˤǤ���褦�ˤʤä�.
�Ǥϡ����η�̤ˤĤ��Ƥʤˤ����λ�����ͽ�ۤǤ��뤫?
���٤��ä��ꡤ��������Ѥ����ꤷ�ơ������θ��������ʤ�����Ƥߤ�.
�㤨�С�Ʊ����¿���ο�����⤫���ơ����η�ϩ��Ťͤ�ɽ������Ȥ�����
���Τ褦�ʥ���դ�����ˤϤɤ���äƤߤ���褤��.
�� (��������)
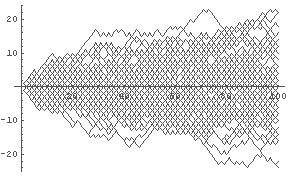 �� ����=���֡� �ļ�= �ơ��㤦����ΰ���(^-^)
�� ����=���֡� �ļ�= �ơ��㤦����ΰ���(^-^)
���ơ��ޤ���ï�Ǥ�狼���ñ��ͽ�ۤ���ˤ��Ƥߤ褦.
�� ���� 1
n ���ο��ʧ����������ʰ��֤Ρ�ʿ���͡פϥ����Ǥ���.
����ϡ������ʡפȡָ���פγ�Ψ�������������Τ����顤�ɤ���ؿʤ�Ǥ���ȹͤ���Τ��Թ��������Ȥ���ľ��Ū�ʹͤ���������Ǥ���.
���ơ������ Mathematica �dz�ǧ���Ƥߤ褦.
RWpath[n][[-1]] (Last[ RWpath[n] ] �ȽƤ�Ʊ��)
�ǿ��ʧ���ˡְ��� n ���⤫�������ΰ��֤���ޤ�Τǡ�
����� m ���餻�Ƥߤ褦.
In[15]:= RWmulti[num_, m_] := Table[ RWpath[num][[-1]], {m} ] �� ����� num ���⤫���롤�Ȥ����Τ� m ��Ԥ�.
���λ��κǸ�ΰ��֤�ơ����Ϥ���.
In[16]:= RWmulti[100, 5] �� 100���⤫���롤�Τ� 5�� ���ᤷ�ˤ�äƤߤ�.
Out[16]= {-2, -14, -16, -4, 10} �� ����ʴ�����.
���ơ�ʿ���ͤ� Mathematica ��
�� ʿ���� �� Mean[���ͤΥꥹ��]
�� �������ƸĿ��dz�����.
�� ������ Needs["Statistics`"]; ��ɬ�ס� �ʤ����⤷��ʤ�.
(�ޥ˥奢��ˡ֤��⤷��ʤ��פȽƤ���(^-^))
�ޡ������äƤ���.
�Ǵ�ñ�˷��Ǥ���ΤǤ����ȤäƤߤ褦.
In[17]:= RWmulti[100, 500]; �� 100���⤫���롤�Τ� 500 ��. �����ˤ�餻���顤��λ�������˿��Ƥ��ޤ�������.
In[18]:= Mean[ %17 ] // N
Out[18]= -0.176 �� �ա��ࡤ�ޤ� 0 �˶ᤤ���Ȥ����ʤ���ʤ���.
In[19]:= Mean[ RWmulti[100, 1000] ] // N �� 100���⤫���롤�Τ� 1000 ��ξ���ʿ�Ѥϡ�
Out[19]= 0.04 �� �ա��ࡤ0 �˶�ʤä��褦�ʵ��������.
���ơ������˲��� 1 �����������ɤ�����������⤫������
(������ʼ¸���������Բ���Ȥ���.
�������ȡ�500 �Ȥ� 1000���Ȥ�����ʬ����������)
���Ѥ��ơ�Ĵ�٤Ƥߤ�.
�� (��������)
�� ��ݡ��Ȳ��� 1
���� 1 ���������.
(n ���ΰ��֤�ʿ���ͤ� loc(n) �Ƚ�loc(n) ��ʬ���äƤ���Ȳ��ꤹ���loc(n+1) �Ϥɤ�������뤫����ͤ���д�ñ )
���ơ�ʿ���ͤˤĤ��Ƥϲ��� 1 �ǥ����å������ΤȤ��ơ�¾�Τ��Ȥ�ͤ��褦.
�������ꥰ��դƤ���ȡ������ư��� 0 ��ˤ������äȤ���ΤǤϤʤ���
�빽�ޤǤ��ޤ褤�⤤�Ƥ������Ȥ�����ʬ����.
���Τ��ޤ褤�⤭�Ρ����١פ��Τ�ˤϤɤ�������褤��������?
ʿ�ѤǤϡ��⤤�Ƥ��ä����̤��ץ饹�ޥ��ʥ����Ǥ��ä���Ƥ����������٤������ʤ��ʤäƤ��ޤ�.
�����ǡ�n ���ΰ��֤Ρ������͡פ����������̤�ȤäƤߤ褦.
����ʤ�ץ饹�ޥ��ʥ����Ǥ��ä���뤳�ȤϤʤ�.
���ؤˤϤ������������������̤�����.
�� ʬ��
��ΨŪ����(�㤨�С������ n ���ΰ���)��ʬ���Ȥϡ�
(�� - ʿ����)2
��ʿ���ͤΤ��ȤǤ���.
�� �פ���ˡ�ʿ�Ѥ���Υ������褬���������狼��Ȥ������Ȥ�.
�� ɸ���к�
��ΨŪ���ͤ�ɸ���к��Ȥϡ�
��(ʬ��)
�Τ��ȤǤ���.
�� �פ���ˡ�ʿ�Ѥ���Υ��줬(�����ͤ�)���������狼��Ȥ������Ȥ�.
(����!!)
�¤ϡ����ʬ����ɸ���к�������ϳ�ΨŪ���ͤ�Ȥ��̤��Τ�Ρ����Ф�������Ǥ��ꡤ
�����̤��ºݤ˼���������ץ��ͤν��硤�Ĥޤꡤ����ο�������ʤɡ�
���Ф��Ƥϰۤʤ������ʬ��, ɸ���к����Ѥ������������ȹ��Թ�Ǥ��뤳�Ȥ��Τ��Ƥ���.
���Τ��ᤫ��Mathematica ���ȹ��ޤ�Ƥ���ʬ����ɸ���к��δؿ���
�֥���ץ��ͽ����ѡפˤʤäƤ��ꡤ�������Ȥϰۤʤ�.
�������������������ͳ��������ˤϤ����ֽ�����ɬ�פʤΤǡ�
����Ϥ���ñ�������Τ�Τ������ˤȤɤ��.
���ʤߤˡ����ΰ㤤�����˾�������n �� �� �ǥ����ˤʤ�Τǡ��ºݡ�
����ϵ��ˤ���ۤɤǤ�ʤ�.
����ɸ���к���Ȥ��С����㤬���������ɤ��ޤǤ��ޤ褤�⤤�Ƥ��äƤ���Τ���
�������٤����Ǥ���.
�����ǡ�ɸ���к��������ؿ����äƻȤäƤߤ褦.
In[20]:= SD[a_] := (
Apply[Plus,
Map[(# - Mean[a])^2 &, a]
] /Length[a]
)^0.5
�� �����ܤ�ɸ���к��������. ���̤�̵�̤�����.
In[21]:= SD[ RWmulti[100, 500] ] �� 100���⤯�Τ� 500���餻�Ƥߤơ��ɤ줯�餤ʿ����(=0)���饺���Τ��Ȥ����ȡ�
Out[21]= 10.4486 �� �������� 10��ʬ���餤�˹ԤäƤ��뤳�Ȥ�¿�����Ȥ������Ȥ���.
In[22]:= RWsd[num_] := SD[ RWmulti[num, 500] ] �� num ���ΰ��֤�ʿ�Ѥ�������ΤΥ��졤���ؿ�.
In[23]:= RWsd[100] �� ���ᤷ�� In[21] ��Ʊ�����Ƥߤ�ȡ�
Out[23]= 9.27146 �� ��������Ʊ���ͤˤʤä�.
���ơ����δؿ� RWsd[���] ��Ȥäơ����㤬�ɤ줯�餤�դ�դ��⤤�Ƥ��ä�������դˤ��Ƥߤ褦.
In[24]:= Table[RWsd[n], {n, 1, 200}]; �� 1 �� 200��ξ��ˤĤ��ơ��ơ��ɤ줯�餤ʿ�Ѥ���Υ��Ƥ��뤫����ꥹ�ȥ��å�.
�빽�����֤�������Τǡ�{n, 1, 200} ����ʬ�� {n, 1, 100, 10} ����ľ���Ƥ�ä������褤����.
In[25]:= ListPlot[%24, PlotJoined -> True]
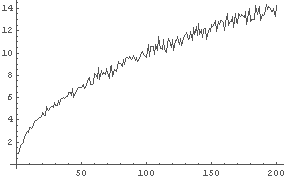 �� ����=���֡� �ļ�=���֤�ɸ���к�=ʿ�Ѥ���Υ���
�� ����=���֡� �ļ�=���֤�ɸ���к�=ʿ�Ѥ���Υ���
�ۤ�.
�������Ƥߤ�ȡ�ʿ��(����ϥ���)����Ρ֥���ס����ʤ��ɸ���к������ n �Ȥ�����Ȥ����ط������ꤽ����.
�Ǥϡ����δط���Ĵ�٤Ƥߤ褦.
��������������դˤ��줤�ʴط�������Ȥ��ϡ��п�����աפ�ľ���Ƥߤ���
�Ȥ����Τ����Ĥ��Ŵ§�ʤΤǡ��������Ƥߤ褦.
In[26]:= LogListPlot[%24, PlotJoined -> True] In[27]:= LogLinearListPlot[%24, PlotJoined -> True]
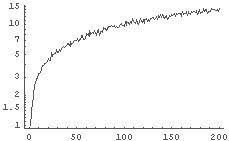
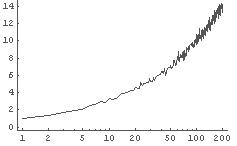 �� y �����п���. ������ʤ����. �� x �����п���. ������ʤ����.
In[28]:= LogLogListPlot[%24, PlotJoined -> True]
�� y �����п���. ������ʤ����. �� x �����п���. ������ʤ����.
In[28]:= LogLogListPlot[%24, PlotJoined -> True]
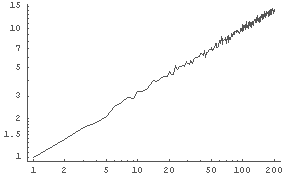 �� x, y ����ξ�����п���. ���������줤��ľ����!!
�� x, y ����ξ�����п���. ���������줤��ľ����!!
�������������
�� �ǡ����Υ���դ����п�(�п��� = x��)������ �� LogLinearListPlot[�ꥹ��]
�� x ���������п��ˤ�������դ�����.
�� Needs["Graphics`"]; ������˹Ԥ�ɬ�פ���.
���Ѥ��Ƥ���.
���ơ�ξ�п�����դ�ȡ����줤��ľ���δط������Ƽ���.
�Ĥޤꡤ����ط����Ȥ������ȤǤ���.
����ط��Ȥ������Ȥϡ�������ɽ�碌�С�
log(y) �� a * log(x) + b �� y �� eb * xa
�Ȥ������Ȥ����顤�ʤ�Ȥ����Ƥ��� a,b �����Ф��ʤ�٤������Ȥ�����Ȥ��Ƹ����뤳�Ȥˤʤ�. �����ǡ��������ä��֥���վ�Υ�������ξ����ͤ�Ĵ�٤�ƥ��˥å��� ��Ȥäơ�����ľ����������ۤɺ�ɸ�äƤߤ�ȡ�
(log(x), log(y)) �� (1, 0.5),
(log(x), log(y)) �� (2, 1)
��������������(�������¾�κ�ɸ�äƤ�褤). ������μ����������Ƥߤ�ȡ�
0.5 �� a * 1 + b
1 �� a * 2 + b
�Ȥ������ȤǤ��뤫�顤����� a �� 1/2, b �� 0 �Ȥ������ȤǤ��ꡤ�Ĥޤꡤ y �� x1/2 �Ȥ������Ȥˤʤ�. ��ǧ�Τ��ᡤ������������դȼ¸�����դ���٤Ƥߤ褦.
In[29]:= DisplayTogether[
LogLogListPlot[%24, PlotJoined -> True],
LogLogPlot[x^0.5, {x, 1, 200}, PlotStyle -> Hue[0]]
]
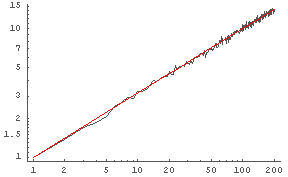 �� y = x1/2 ���֤ǰ��˥���ղ�. �ۤܰ��פ��뤳�Ȥ��ɤ�ʬ����.
In[30]:= DisplayTogether[
ListPlot[%24, PlotJoined -> True],
Plot[x^0.5, {x, 1, 200}, PlotStyle -> Hue[0]]
]
�� y = x1/2 ���֤ǰ��˥���ղ�. �ۤܰ��פ��뤳�Ȥ��ɤ�ʬ����.
In[30]:= DisplayTogether[
ListPlot[%24, PlotJoined -> True],
Plot[x^0.5, {x, 1, 200}, PlotStyle -> Hue[0]]
]
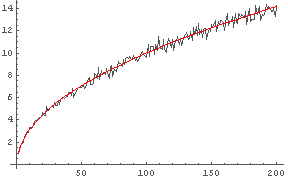 �� �п��Ǥʤ������. ��Ϥ�ۤܰ��פ��뤳�Ȥ��ɤ�ʬ����.
�� �п��Ǥʤ������. ��Ϥ�ۤܰ��פ��뤳�Ȥ��ɤ�ʬ����.
�����������
�� �ؿ���ξ�п�����դ����� �� LogLogPlot[�ؿ����ϰ�]
�� x, y ��ξ�����п��ˤ�������դ�����.
�� Needs["Graphics`"]; ������˹Ԥ�ɬ�פ���.
���Ѥ��Ƥ���.
���ơ�����ǿ��ʧ�����㤬 n ����ʿ����(= 0)����ɤ줯�餤Υ��Ƥ��뤫��
�ˤĤ��Ƥ��ʤ����Τʲ��⤬���Ƥ���.
�� ���� 2
n ���ο��ʧ������ΰ��֤�ɸ���к��ϡ��ۤ� n1/2 �Ǥ���.
(�Ĥޤꡤ����˥���Ƥ���Ȥ��ơ����Υ�������٤� n1/2 �Ǥ���.)
�� ��ݡ��Ȳ��� 2
���� 2 ������Ω�Ĥ櫓����������.
(�������ȤޤǤϤ����ʤ��Ƥ������ϡ��Ȥ�����٥�)
��Ǽ����������ˤ���Ψʬ�۷����Ѥ���Τ��ɤ�.
��������Taylor Ÿ�����ο���Ūƻ��ɬ�פˤʤ�� ����.
��μ�����β���Ȥ���Ϳ�����Ƥ���褦��
��¿���ο��㤬�⤤����ϩ��Ʊ��ɽ�����륰��ա�
�ȡ����β���η�̤�դǽŤ�碌�ơ��ɤ��ʤ뤫���Ƥߤ�.
�� (��������)
���ơ���������ο���ΰ��֤γ�Ψʬ��( n ���ˡ����� x �ˤ����Ψ)�Ϸ��ϤǤ��ʤ��Τ�������? �¤ϡ���ñ�ʷ����֤����Ȥǵ��뤳�Ȥ��Ǥ���ΤǤ���. ����ˤϡ�10000 �ͤο��㤬�㤨��Ʊ�����⤭�Ф����ȹͤ��Ƽ��Τ褦�ʿޤ�ͤ����ʬ����䤹��.
����= n ʬ n+1 ʬ n+2 ʬ n+3 ʬ
(��) ���
| | | | Q/
0 + 0 + 0 + -�� 1250 + /|
| | | �� | < >
| | | ��* 0.5 |
| | | �� | Q/
0 + 0 + -�� 2500 + 0 + /|
| | �� | �� | < >
| | ��* 0.5 | ��* 0.5 |
| | �� | �� | Q/
0 + -�� 5000 + 0 + -�� 3750 + /|
| �� | �� | �� | < >
| ��* 0.5 | ��* 0.5 | ��* 0.5 |
Q/ | �� | �� | �� | Q/
Oyaji /| �� 10000 + 0 + -�� 5000 + 0 + /|
< > | �� | �� | �� | < >
| ��* 0.5 | ��* 0.5 | ��* 0.5 | ������
| �� | �� | �� | Q/
0 + -�� 5000 + 0 + -�� 3750 + /|
| | �� | �� | < >
| | ��* 0.5 | ��* 0.5 |
| | �� | �� | Q/
0 + 0 + -�� 2500 + 0 + /|
| | | �� | < >
| | | ��* 0.5 |
| | | �� | Q/
0 + 0 + 0 + -�� 1250 + /|
| | | | < >
(��)
�� ��
�Ϳ� �Ϳ�Ū�ˤ����֤Ф餱��
��������ο����äѤ�ä��⤭�ޤ��ο�
���οޤ�¨���ƹͤ���С�n ���(n ʬ��) �˰��� x �ˤ���Ϳ���
f(x,n)
�Ȥ���ȡ�
0.5 * f(x-1,n) + 0.5 * f(x+1, n) = f(x, n+1)
�Ȥ���������������Ω�Ĥ��Ȥ�ʬ����.
f �����Ϳ��dz��г�Ψ�ȸ��ʤ����ɤ����������顤��ɡ�
n ���(n ʬ��) �˰��� x �˿��㤬�����Ψ P(x, n) ��
P(x, n+1) = 0.5 * P(x-1,n) + 0.5 * P(x+1, n)
�� n = 0 �����˷����Ƥ����Ф褤���Ȥ������Ȥˤʤ�.
(��) ���� = 0 �Ǥϡ�����ϸ��� x = 0 �˳�Ψ 1 ��¸�ߤ���.
�����ǡ������������˽��äƷ���ʤ��ؿ�������.
n ���(n ʬ��)�ο����¸�߳�Ψ��ꥹ�Ȥˤ���
�ꥹ�� a(n) = {P(-m, n), P(-m+1, n),��, P(-1, n), P(0, n), P(1, n),��, P(m, n) }
���Ф��ơ�
RWonedist[ a(n) ] �Ȥ���� a(n+1) �����Ϥ����褦�ˤ��褦.
In[31]:= RWonedist[a_] := Module[{num, b, result},
num = Length[a];
b = Append[Prepend[a, 0], 0]; �� a(n) ������˥�����Ĥ��ơ������ϰϤ�̷�⤬�ʤ��褦�ˤ��Ƥ���.
result = Table[0.5 * b[[n - 1]] + 0.5 * b[[n + 1]], {n, 2, num + 1}];
�� ���줬����������ˤ���.
Return[result]
]
In[32]:= RWonedist[{0, 0, 0, 1, 0, 0, 0}] �� ���ᤷ�˾�οޤΰ��ֺ�¦�������äƤߤ�ȡ�
Out[32]= {0, 0, 0.5, 0, 0.5, 0, 0} �� ����!
In[33]:= RWonedist[%] �� ³����ȡ�
Out[33]= {0, 0.25, 0, 0.5, 0, 0.25, 0} �� ������οޤ��̤�.
In[34]:= RWonedist[%] �� �����³����ȡ�
Out[34]= {0.125, 0, 0.375, 0, 0.375, 0, 0.125} �� ����⤢�äƤ���.
�����������
�� �ꥹ�� ����Ƭ�����Ǥ�ä��� �� Prepend[�ꥹ��, ����]
�� Prepend[{a,b}, x] �� {x, a, b} ����Ϥ���.
���Ѥ��Ƥ���.
����ǡ�����ͤȤ��� ¸�߳�Ψ�Υꥹ�� ���Ѱդ��ơ�RWonedist �� n ��Ŭ�Ѥ������
n ʬ���¸�߳�Ψ�Υꥹ�Ȥ������뤳�Ȥˤʤ�.
��äơ����������ؿ���(0 �� n ʬ��ޤǤη�̤������Ф��褦�˺�ä�)
RWdist[����ͥꥹ��, ���] �Ȥ����Ѱդ��褦.
In[35]:= RWdist[a_, num_] := NestList[ RWonedist[#]&, a, num ]
In[36]:= RWdist[{0, 0, 0, 1, 0, 0, 0}, 3] �� ���ᤷ�˾��Ʊ�����Ȥ��äƤߤƳ�ǧ.
Out[36]= {{0, 0, 0, 1, 0, 0, 0}, {0, 0, 0.5, 0, 0.5, 0, 0},
{0, 0.25, 0, 0.5, 0, 0.25, 0}, {0.125, 0, 0.375, 0, 0.375, 0, 0.125}}
����ǡ�����Τ�����γ�Ψʬ�ۤ�ľ�ܷ��Ǥ��롤�Ȥ������Ȥˤʤä�.
���ơ������ǤϿ���Τ�����֤� 7�Ľꤷ���ͤ��ʤ��ä���������Ǥ϶�������Τǡ�
100�Ľ����٤˹����ơ����������Ƥߤ褦.
In[37]:= Table[0, {99}] �� 99 �Ĥ� 0 ���¤֥ꥹ��.
Out[37]= ����
In[38]:= a = ReplacePart[%, 1, 50] �� �����������Ψ�� 1 ��ľ���ơ�����ͥꥹ�ȡ��Ȥ���.
Out[38]= {0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}
In[39]:= RWdist[a, 200] �� 200 ���(ʬ��)�ޤǤ�¸�߳�Ψʬ�ۤ��.
Out[39]= {{0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,
����
0.00101877, 0, 0.000666154, 0, 0.00041809, 0, 0.000241867, 0, 0.000110277, 0}}
In[40]:= ListPlot[%39[[-1]], PlotStyle -> PointSize[.01], PlotRange -> All]
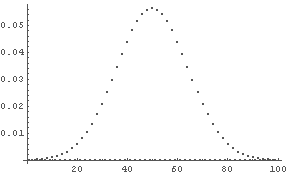 �� 200 ʬ��γ�Ψʬ�ۡ����줤��ʬ�ۤ�.
In[41]:= Table[
ListPlot[
%39[[n]],
PlotStyle -> PointSize[.02],
PlotRange -> All
],
{n, 50, 200, 50}
]
�� 200 ʬ��γ�Ψʬ�ۡ����줤��ʬ�ۤ�.
In[41]:= Table[
ListPlot[
%39[[n]],
PlotStyle -> PointSize[.02],
PlotRange -> All
],
{n, 50, 200, 50}
]
 �� 50,100,150,200 ʬ��γ�Ψʬ�ۡ�������Ʊ�������������������������Τ��褯�狼��.
�� 50,100,150,200 ʬ��γ�Ψʬ�ۡ�������Ʊ�������������������������Τ��褯�狼��.
����ǡ���Ψʬ�ۤ����Ǥ���Τǡ����㤬 n ʬ��˰��� x �ˤ����Ψ����̩��ʬ���롤�Ȥ�����Τ�.
����������ʤΤϡ�
��ΨŪ�ʸ��ݤε�ư���������Ȥ鷺�˷��Ǥ���
�Ȥ������ȤǤ���.
��̩�˸����С��������ˤ�äƵ�ޤ�Τϡ��֤�������ο���ε�ư��ʿ�ѡ�
�ȤǤ⤤���٤���Τǡ��֤�������ο���ε�ư�פ��Τ�Τ��ɤ���櫓�ǤϤʤ�.
����������̣�ǡ���Ψʬ�ۤΥ����(= �������ǵ����)�����뤳�Ȥ�
�ּ夤������פȤ�����
�ƿ�����⤯��ϩ��ơ����뤳�Ȥ�
�ֶ���������פȤ��äƶ��̤���.
�㤨�С��ַ�� ���㤬�����Ǥɤ줯�餤�⤯�Τ��פȤ����褦������ϡ�
�ּ夤��פǤ��������Ǥʤ�.
���ä�����Ψʬ�ۤ������ͤ����Ǥ����Τǡ�����ȼ¸��ͤ���Ӥ���.
�� (��������)
# n ʬ��� ���� x �˿��㤬�����Ψ�������͡��ȼ¸��Ǥ����٤���٤Ƥߤ�ʤɤ���Ф褤.
# �ٿ�ʬ�ۤ�Ȥä���Ӥ���Ф�äȤ褫����.
���ơ����ä������������Ƥ���Τǡ������η�̤���٤�ɽ�����Ƥ�����.
���줫��ⲿ���θ����������������
In[42]:= ListPlot3D[%39, PlotRange -> All]
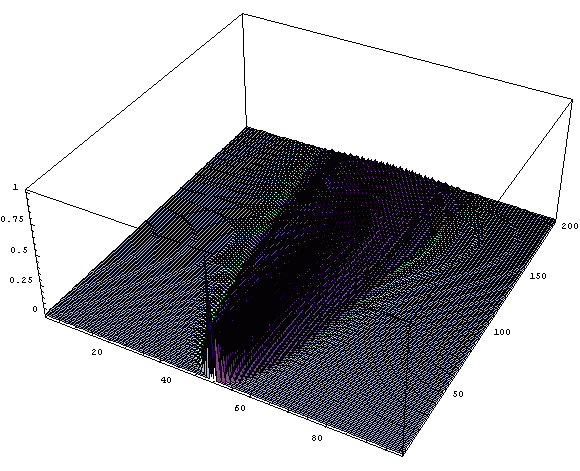 �� ��Ψʬ�ۤ����֤Ǥɤ��Ѳ����Ƥ����������ܤǸ�����.
�� ��Ψʬ�ۤ����֤Ǥɤ��Ѳ����Ƥ����������ܤǸ�����.
�����������δؿ����Ѥ��Ƥ���.
�� 3 �����ǡ����Υ���դ����� �� ListPlot3D[3�����ǡ����ꥹ��]
�� �ǡ����ꥹ�Ȥϡ��⤵��ɽ�魯�¿���Ĺ������Ǥʤ��Ȥ����ʤ�.
���ơ���� In[41] �ǤΥ���դϳ��������Ƥ���.
����ñ�̤��Ѥ���Ф��ä���ǤϤʤ�������.
�����������? �����ơ��ʤ�������?
�ޤ���������Ѥ����ҥ��ȥ�����Ȥäơ����������ͤ��ɤ줯�餤�¸��ͤȤ�����Τ����ܤ�ľ�ܸ��Ƹ��ڤ��褦.
����ˤϡ������
FreqRate[a_] := Map[
{ N[ #[[1]]/Length[a] ], #[[2]] }&,
Frequencies[a]
]
IRHistogram[a_] := BarChart[ FreqRate[a] ]
��Ƥ�Ƴ�����ơ��ȤäƤߤ�.
In[43]:= RWmulti[200, 500]; �� 200���⤫���롤�Τ� 500 ��.
In[44]:= IRHistogram[ % ]
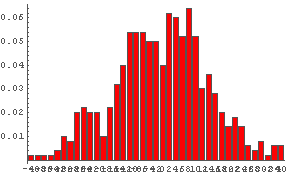 �� ���㤬 200���ˤɤ��ˤ���Τ�. ���γ�Ψʬ��(�¸���).
�� ���㤬 200���ˤɤ��ˤ���Τ�. ���γ�Ψʬ��(�¸���).
In[44] �η�̤� In[40] �η�̤���Ӥ���С������ͤȼ¸��ͤ���Ӥ��Ǥ���.
��äƤߤ�. �� (������β���)
���ơ������¿���μ¸���̤�ʬ�ۤ�ߤƤߤ�ȡ�
In[45]:= Table[
IRHistogram[ RWmulti[n, 500]],
{n, 50, 200, 50}
]
 �� 50,100,150,200 ʬ��γ�Ψʬ�ۼ¸��͡��������ۤ�Ʊ����.
�� 50,100,150,200 ʬ��γ�Ψʬ�ۼ¸��͡��������ۤ�Ʊ����.
�ޤ�����η�̤� In[41] �η�̤���Ӥ���.
�����ȼ¸��Ϥ���ʤ�˹礦������������ (������β���)
�� ��ݡ��Ȳ��� 3
����� In[42] ����������¸���̤Υ���դ��������In[42] �Υ���դ���Ӥ���.
���ơ���η�̤�ȡ�����Τ�����֤γ�Ψʬ�ۤμ¸��ͤϷ���Ū�ˤ�Ʊ�������˻���Ф�褦��.
�����⡤���η����Ϥɤ����Ǹ����褦�ʷ��Ƥ���.
�褯�פ��Ф��ȡ����������� 4���⤷���ϡ��濴�˸������פθĽ�ǤǤƤ�������դˤ��Υ���դϤ��ä���Ǥ���.
����϶�����������?
�ͤ��Ƥߤ褦.
���������䤹�ʤɤ��ơ�Ʊ�ͤ�Ĵ�٤Ƥߤ褦. �� (������β���)
�� ��ݡ��Ȳ��� 4
�������줿����դ����������� 4���⤷���ϡ��濴�˸������פθĽ�ǤǤƤ�������դˤ褯���Ƥ���.
������ͳ��Ҥ٤�.
(���㤬 n ���ˤ�����֤Ȥϡ� +1 �� -1 �ˤʤ������ n ��������ΤǤ��롤�ȹͤ���ȡ�)
���ơ����Υ���դ��濴�˸������Ȥδط�����ͳ�ϥ�ݡ��Ȥǹͻ�����Ȥ��ơ�
�����(��ͳȴ����)������ʬ�Ҥ��Ʋ���ˤ��Ƥ�����.
�� ���� 3
n ���ο��ʧ������ΰ��֤ϡ��濴�˸������ˤʤ�餫�η��ǽ���.
�Ĥޤꡤ���ΰ���ʬ�ۤη����� n �� �� ���濴�˸������μ������ˤʤ�.
�����⡤���λ���ʿ�Ѥ� ������ɸ���к��� n1/2 �ˤʤ�.
���ơ�����ο��ʧ������ϡ�����ˤ�����ư����,
������ɤ���عԤ���Ψ�� 1/2 ��Ʊ�ͤȤ�����ñ�ʿ�����ä�(^-^).
�Ǥϡ��⾯����䤳��������ξ��ϡ�������Ƥβ��ϤϤɤ��ʤ��������?
�㤨�С�
���عԤ���Ψ = 1/3,
�ȤɤޤäƤ����Ψ = 1/3,
����عԤ���Ψ = 1/3
���ä���ɤ��ʤ������?
¾�ξ���?
�� ��ݡ��Ȳ��� 5
Ŭ���˿���ε�ư�����ꤷ�ơ���ʬ�Ǥ��ξϤ�Ʊ�ͤβ��Ϥ�ԤäƤߤ�.
�ۤʤä���̡�Ʊ�����ä���̡��ơ��ˤĤ��ơ��ʤ��ۤʤä��Τ���Ʊ�����ä��Τ�����ͻ�����.