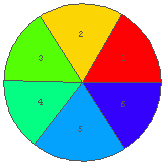
← 仮説 1 のチェックを行うためのグラフ.
In[10]:= DieRPie[a, 2] 
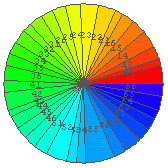← 仮説 2 のチェックを行うためのグラフ.
今回は，ランダムさがもつ性質についてまた違う角度から調べてみよう.
さて，今回は乱数生成装置として「サイコロ」を考えよう. ただし，実際にサイコロをころがして実験するのは労力的に大変なので， Mathematica を使ってサイコロの挙動を再現しよう.
In[1]:= Needs["Graphics`"]; ← 必要になるので，一番最初に忘れないようにやっておく.
In[2]:= Needs["Statistics`"]; ← これも必要になる. 詳しくは後述.
これを事前にやるのを忘れるといろいろ厄介なので忘れないように!!
In[3]:= Die[] := Random[Integer, {1,6}] ← 1 〜 6 の数字をランダムに作る乱数. 特に引数は無い.
In[4]:= Die[]
Out[4]= 3 ← 一回サイコロを振ってみる.
In[5]:= Die[]
Out[5]= 5 ← もう一回サイコロを振ってみる. もちろん振る度に値が変わる.
In[6]:= Table[ Die[], {10}]
Out[6]= {2, 5, 1, 4, 6, 6, 1, 2, 2, 5} ← 10回 サイコロを振ってみた.
として，サイコロを Die[ ] という関数で再現することにする.
さて，まずはサイコロがサイコロらしい性質を持っているかどうかチェックしてみよう.
といっても難しいことをするわけではない.
前回の仮説 1 〜 4 が正しいと仮定して，仮説を満たすかどうかおおまかにチェックするだけでよい.
つまり，
ListToString[a_] := Apply[StringJoin, Map[ToString, a]];
Rate[whole_, str_] := Module[{num, lwhole, lstr},
lstr = StringLength[str];
lwhole = StringLength[whole];
num = Length[StringPosition[whole, str]];
Return[num/(lwhole - lstr + 1) // N];
]
は再利用して，また，二文字だけからなる場合の
BinComb[num_] := Map[StringJoin,
Distribute[Table[{"0","1"}, {num}], List]
]
BinRate[whole_, num_] := Module[{bcomb},
bcomb = BinComb[num];
Return[{Map[Rate[whole, #] &, bcomb], bcomb}]
]
BinRPie[whole_, num_] := Module[{brate},
brate = BinRate[whole, num];
PieChart[brate[[1]], PieLabels -> brate[[2]] ];
] ← ここの PieChart が Graphics パッケージを必要とする.
はちょっとずつ修正して，DieComb, DieRate, DieRPie などとサイコロ用に
作り替えて利用すれば良い.
→ (授業中の課題)
ちなみにそういうものを作ってやってみると，
In[7]:= Table[Die[], {500}]; ← 思い切って 500回振ってみた.
In[8]:= a = ListToString[%7]; ← 文字列に直す.
In[9]:= DieRPie[a, 1] ← 仮説 1 のチェックを行うためのグラフ.
In[10]:= DieRPie[a, 2] ← 仮説 2 のチェックを行うためのグラフ.
となるので，このサイコロの出した目は 1文字からなる文字列，
2文字からなる文字列に対しては十分に偏りが少ないと見てよい.
つまり，ランダム性の基準である仮説 1,2 は満たすと言ってよいだろう.
では，仮説 3,4 に対してはどうか?
→ (授業中の課題)
つまり，このサイコロは賭け事に使っても不公平はあまりなかろう，ということである(^-^).
もちろん，賭博は違法であるのでやらないように.
さて，サイコロにいかさまが無いことを確認できたとして，次に移ろう.
今回はまた違う視点からランダム性，乱数の性質に迫ってみるのだが，
今回の視点には円グラフよりも適切なグラフがあるので，そちらを使用しよう.
そのグラフは，
「1」の目が何回出るか，「2」の目が何回出るか… を数えてグラフにする，
いわゆる度数分布グラフ(もしくはヒストグラム)である.
Mathematica にはもちろんそういう機能があるのでそれを使ってみよう.
In[11]:= Table[Die[], {500}]; ← また 500回振ってみた.
In[12]:= Histogram[%11] ← これが Graphics パッケージを必要とする.
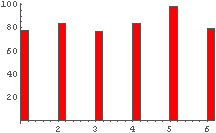← その度数分布グラフ. ヒストグラム. ただ，整数の度数分布を見るにはちょっとカッコ悪いかな.
In[13]:= IntHistogram[a_] := Histogram[a,
HistogramCategories -> Table[n + 0.5, {n, Min[a]-1, Max[a]}]
]
← 普通に Histogram だけだと細くて気持悪いという人用に，
整数の度数分布専用に作ってみると…
In[14]:= IntHistogram[%11]
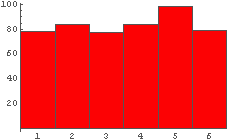← 同じデータで こんな感じ. ちょっと見易くなったかな?
In[15]:= IntHistogram2[a_] := BarChart[Frequencies[a]]
← 整数の分布の場合，どちらかというとこちらが正統派か.
図がちょっと違うだけで，機能は全く同じになるはずだが.
← これが Statistics パッケージを必要とする.
In[16]:= IntHistogram2[%11]
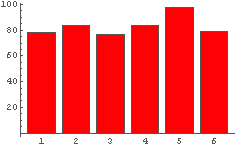← IntHistogram[ ] とちょっとだけ違う(^-^).
サイコロを振る回数を増減して，度数分布がどのように変わるか観察せよ.
→ (授業中の課題)
途中で使った新しい関数は，以下のようなものである.
● 度数分布を調べてグラフにする … Histogram[リスト]
→ 入力したデータリストの度数分布を調べ，かつ，グラフを作ってくれるという「二つの動作」
を同時にしてくれるという珍しいタイプの関数.
度数分布だけを調べたいのであれば，Frequencies(整数分布の場合)や BinCounts(実数分布の場合) を用いる.
→ 度数を調べる範囲をどう刻むかは自動でやってくれる.
指定するには，オプションの HistogramCategories を用いる.
→ どちらかというと実数分布向き.
→ オプション FrequencyData -> True とすると，
データリストが度数分布自身であるとしてグラフにする，という動作に切り替わる.
→ Graphics パッケージの一部.
つまり，Needs["Graphics`"] を事前にやって，パッケージを読み込んでおけということ.
→ ● 度数分布を調べる区間の刻み方を指定する … オプション HistogramCategories
例えば，横軸を
0.5 ≦ x ＜ 1.5,
1.5 ≦ x ＜ 3.5,
3.5 ≦ x ＜ 6.5
と区切って表示したいというのであれば，
HistogramCategories -> {0.5, 1.5, 3.5, 6.5}
とする.
→ ● (既知の)度数分布を図示する … オプション FrequencyData
もう度数分布は調べてある，という場合はこちら.
各々の度数をリストにしたものを用意して，Histogram[リスト, FrequencyData -> True]
とすれば良い.
例えば，次のようになる.
Histogram[{1, 10, 1}, FrequencyData -> True]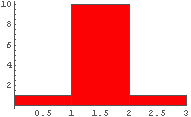 
● 整数データの度数分布を調べる … Frequencies[(整数の)リスト]
→ 整数リストに対して，{出現回数, その数字} を対にしてリストにして出力する.
→ つまり，Frequencies[{3,6,4,5,4}] とすると，
{{1, 3}, {2, 4}, {1, 5}, {1, 6}} が得られる.
→ Statistics (統計)パッケージの一部.
要するに，事前に Needs["Statistics`"] が必要.
● 最大値，最小値 … Max[リスト], Min[リスト]
→ リストの要素を比較して最大値，最小値を出力する.
● 度数分布をグラフにする … BarChart[数字対のリスト]
→ {高さ, 横軸座標} の対をリストにしたものを入力すると，
その座標にその高さのバーを描いてグラフを作成する.
上の Frequencies と合わせれば整数用ヒストグラム関数の出来上がりである.
→ Graphics パッケージの一部.
つまり，Needs["Graphics`"] が事前に必要.
本質的には上記 3つの関数は働きが同じなので，
これ以降どのヒストグラム関数を用いても良い(見掛けで選んで好きなものを使えば良い).
さて，本題に戻ろう.
上に示したサイコロを使って賭事をするとしよう.
繰り返すが，博打は違法である.
今回の話はあくまでも分かりやすくするための例え話であるので誤解なきよう(^-^).
まず，このサイコロ一つを振ってどの数字が出るか賭ける，というシステムを考える.
しかし，これはどの数字が出るか確率はどれも均等に 1/6 なので，
合理的に考えて「予想」が働く余地は全くない.
そのため，実際には賭事としては成立しにくいだろう.
# もちろん，サイコロを振る際の「いかさま」等はないものとして.
(注意)
例えば，「1」が続けて二回出たから次は「1」は出にくいだろう，というのは合理的な予想ではない.
それは「思い込み」とか「勘違い」などと呼ばれるものである.
□ レポート課題 1
上の注意が正しいかどうか，実際にチェックしてみよ.
(つまり，「1」が続けて二回出た後にどの数字がでるか，その頻度を比べてみれば良い)
そこで，サイコロを 2つ使うことにしよう.
サイコロを 2つ同時に振り，その数字の合計がいくつになるか賭ける，
というシステムを考えてみる.
そこで，n 個のサイコロを同時に振って，でた数字の合計を求める関数を作っておこう.
In[17]:= Dice[num_] := Table[Die[], {num}] ← 同時に num個のサイコロを振る関数.
In[18]:= Dice[3]
Out[18]= {3, 5, 5} ← ためしに 3個振ってみた.
In[19]:= DiceSum[num_] := Apply[Plus, Dice[num]] ← 同時に num個のサイコロを振って，出た数字を合計する.
In[20]:= DiceSum[5]
Out[20]= 22 ← ためしに 5個振って，その合計を出してみた.
これで 2個サイコロを同時に振ってその合計を求めるのは DiceSum[2] で済む. 早速，どの数字に賭けたら有利なのか，どの数字が大穴なのか調べてみよう(^-^).
In[21]:= Table[ DiceSum[2], {500} ] ← サイコロ2個同時投げ，を 500回やってみる.
Out[21]= …略…
In[22]:= IntHistogram[%]
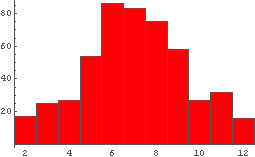← 500回のサイコロ2個投げの分布の様子.
ふむふむ，数字の合計が 6〜8 あたりが頻度が最も高い = もっとも出やすい
ということがなんとなくこれだけでも見て取れる.
少なくとも次にどの数字がでるか「予想」する価値はありそうだ.
しかし，その数字が出る確率を求めるにはこの度数分布グラフではちょっと不便だ.
そこで，細かい調査を行うためにも確率分布のグラフに直して表示してみよう.
それには，自動的にグラフになってしまう Histogram や IntHistogram
は使えないので，いったん度数分布を求めている IntHistogram2 を改良する，ということになる.
In[23]:= FreqRate[a_] := Map[
{ N[ #[[1]]/Length[a] ], #[[2]] }&,
Frequencies[a]
] ← 度数分布を求めてから，それを全体の数で割っているだけ.
In[24]:= Frequencies[%21] ← 例えば，上のサイコロ2個投げ，の度数分布はこうなって…
Out[24]= {{17, 2}, {25, 3}, {27, 4}, {54, 5}, {86, 6}, {83, 7},
{75, 8}, {58, 9}, {27, 10}, {32, 11}, {16, 12}}
In[25]:= FreqRate[%21] ← 確率分布はこうなる. 度数が 500 で割られているだけ，だ.
Out[25]= {{0.034, 2}, {0.05, 3}, {0.054, 4}, {0.108, 5}, {0.172, 6}, {0.166, 7},
{0.15, 8}, {0.116, 9}, {0.054, 10}, {0.064, 11}, {0.032, 12}}
In[26]:= IRHistogram[a_] := BarChart[ FreqRate[a] ]
← 求めた確率分布を棒グラフにするだけ.
In[27]:= IRHistogram[%21]
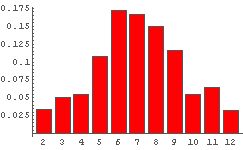← 上のサイコロ2個投げの確率分布. 縦軸がちゃんと確率になっているのに注意.
これでどの数字がでる確率がいくつ，ということが目で見てわかる.
これを使っていろいろ調べることができよう.
(授業中の課題) → 何回かやって真の確率分布がどうなっているか，推測せよ.
さて，サイコロ2つの目の合計がどれくらいの確率で出るか，はいくらなんでも簡単すぎて，小学生でも計算できるというものだ.
まず，2つの数字の組み合わせは全部で 6 x 6 = 36 通り.
で，例えば 合計が 4 になる組み合わせは {サイコロ1, サイコロ2} = {1, 3} {2, 2} {3, 1} の 3通り.
だから，2個のサイコロの数字の合計が 4 になる確率は 3/36 = 1/12 (= 0.083333…)
である.
そこで，理論的な確率分布を一緒に表示しておこう.
In[28]:= Table[Min[n - 1, 13 - n] / 36, {n, 2, 12}]
Out[28]= {1/36, 1/18, 1/12, 1/9, 5/36, 1/6, 5/36, 1/9, 1/12, 1/18, 1/36}
← 2個のサイコロの目の合計が各々 2 〜 12 である確率.
In[29]:= DisplayTogether[
IRHistogram[%21],
ListPlot[
%28,
PlotStyle -> {
Hue[0.6],
PointSize[.03]
}
]
]
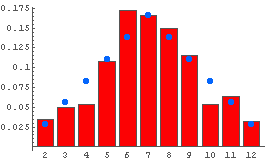← 上のサイコロ2個投げの実際の確率分布(赤い棒グラフ)と理論値(青い点).
ただし途中で次の関数を用いている.
● 複数のグラフを一つのグラフにまとめて表示する … DisplayTogether[プロット関数1, プロット関数2, …]
→ 使い方は簡単.
普通にグラフを描く命令を並列に並べるだけ，だ.
→ 座標は共通なので，その点は注意.
まあ，描いてみればわかるか.
→ Graphics パッケージの一部.
つまり，Needs["Graphics`"] が事前に必要.
さて，今回は理論値が求まっているからそれを使えばいいが，
そうでないときは実験を繰り返すなどして確率分布を推定し，
それをもとにどの数字に賭ければ良いか考えるのである.
# もちろん，当たったときの配当率やリスク分散を勘案する必要はある(^-^).
さて，少し息抜きをしてみよう.
この賭けの胴元が，配当率を次のように設定してきた.
| サイコロ2個の数字合計 | 2 or 12 | 3 or 11 | 4 or 10 | 5 or 9 | 6 or 8 | 7 |
|---|---|---|---|---|---|---|
| 配当率(返金倍率) | 30.0 | 10.7 | 6.5 | 4.6 | 3.6 | 3.0 |
そして，貴方は毎回一回の賭けで合計 10円(^-^;) を賭けることにしているとする.
いろいろ考えた挙げ句，貴方はその大事な 10円を次のように手堅く分配して賭けることにした.
# この賭け方がいいか悪いかはまた後で検討するとして.
| サイコロ2個の数字合計 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 賭け金 | 0 | 0 | 0 | 1 | 2 | 4 | 2 | 1 | 0 | 0 | 0 |
さて，配当率，賭け金を各々関数 Div[ ], Bet[ ] とし，
一回の賭けで得られる利益を Obtain[2個のサイコロの数字合計]
として作ってみる.
In[30]:= Div[num_] := Module[{lst},
lst = {30.0, 10.7, 6.5, 4.6, 3.6, 3.0};
Return[ lst[[ Min[num-1, 13-num] ]] ]
] ← 配当率の関数.
In[31]:= Table[ Div[n], {n,2,12} ]
Out[31]= {30., 10.7, 6.5, 4.6, 3.6, 3., 3.6, 4.6, 6.5, 10.7, 30.} ← 確かにあっているか確認.
In[32]:= Bet[num_] := Module[{lst},
lst = {0,0,0,1,2,4,2,1,0,0,0};
Return[ lst[[num-1]] ]
] ← 賭け金の関数.
In[33]:= Table[Bet[n], {n, 2, 12}]
Out[33]= {0, 0, 0, 1, 2, 4, 2, 1, 0, 0, 0} ← 確認.
In[34]:= Obtain[num_] := Div[num]*Bet[num]- Sum[Bet[n], {n,2,12}] ← 利益 = 取得したお金 - 投資(^-^)
In[35]:= Table[ Obtain[n], {n, 2, 12} ]
Out[35]= {-10, -10, -10, -5.4, -2.8, 2., -2.8, -5.4, -10, -10, -10} ← 各々，どの数字になったらいくら儲かるか(^-^).
7 が出ない限り損だ.
さて，何回か賭け,利益を得る，という動作を Bets[回数] という関数でまとめるとして貴方の所持金がどう増減するか，チェックしてみよう.
In[36]:= Bets[num_] := Module[{d, hist},
d = Table[ DiceSum[2], {num}] ; ← サイコロを num 回振っての結果リスト.
hist = Map[ Obtain[#]&, d]; ← その瞬間得た利益の履歴リスト.
Return[ { hist, d } ]
] ← {利益履歴リスト，結果リスト} を出力.
In[37]:= Bets[10]
Out[37]= {{-10, -2.8, -10, -5.4, -2.8, -10, -10, -2.8, -10, 2.},
{3, 8, 4, 5, 6, 10, 2, 8, 2, 7}}
← ためしに 10回やってみた.
さて，長期的な目で見て貴方はこの賭けで儲かるか，それとも損をするだろうか. Bets の結果を「その時点での合計利益」の経過に直してみよう.
In[38]:= Summation[a_] := Table[
Sum[a[[j]], {j, 1, n}],
{n, 1, Length[a]}
] ← 新しいリストの n 番目の要素 = a[1] + a[2] + … +a[n] としている.
In[39]:= Summation[ %37[[1]] ]
Out[39]= {-10, -12.8, -22.8, -28.2, -31., -41., -51., -53.8, -63.8, -61.8} ← 上の結果に対してやってみた. これが利益の累積経過，である.
□ レポート課題 2
上の Summation 関数はわかりやすさを優先したため，計算量には無駄がある.
この方法のどこがどう無駄で，どう改善すればよいか示せ.
さて，この Summation を用いて，この賭けによる累積利益の長期経過を見てみよう.
In[40]:= Summation[ Bets[100][[1]] ] ← 100回賭け続けてどうなるか…
Out[40]= {2., -8., -10.8, -16.2, -19., -24.4, -22.4, -32.4, -30.4, -28.4,
…略…
-529.2, -534.6, -540., -538., -540.8, -546.2, -556.2, -566.2}
In[41]:= ListPlot[%40, PlotJoined -> True]
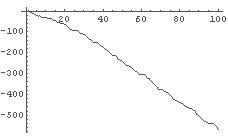← 100回賭け続けた場合の利益の経過. 一方的に損が増えていく(負けがこむ)ことが分かる.
さて，このグラフを見ると，直線的にきれいに下がっていることが見て取れる.
つまり，累積利益と賭けた回数にはきれいな関係がある，ということを示唆している.
これを簡単に言い換えると次のようになる.
■ 仮説 1
この賭けに対し，上記の配当率と賭け金のもとで n 回賭けた時の利益はおよそ αn 円である. ただし，α < 0 .
この仮説を検証するにはどうしたらよいか.
理論的に解析 & 証明する方法と実験を用いる方法があるが，理論の方はレポートにするとして，
実験を行ってみよう.
今回の検証には，α に相当する数字をグラフで直接表示するのがもっとも簡単だろう.
In[42]:= Table[ %40[[n]]/n, {n, 1, Length[%40]} ]
Out[42]= {2., -4., -3.6, -4.05, -3.8, -4.06667, -3.2, -4.05, -3.37778, -2.84,
…略…
-5.68421, -5.60417, -5.57526, -5.57347, -5.61818, -5.662}
In[43]:= ListPlot[%42, PlotJoined -> True]
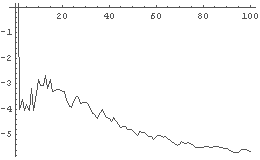← 累積利益/賭け回数の経過. 一定値に近づいているように見える.
(授業中の課題) → α がいくつぐらいなのか，実験を何度か行い，推測せよ.
□ レポート課題 3
仮説 1 を理論的に検証せよ.
また，α がいくつぐらいが妥当なのか理論的に示せ.
今回の賭け方ではどうも損が大きいような印象があるが，ではどうやったら損を小さく，もしくは儲けることができるか.
それをよく考えてみると良い → レポート.
□ レポート課題 4
上の賭けに対し，上記の配当率のもとでどう賭けたらもっとも累積利益を大きくできるか考えよ.
(もっとも損しない，と言い換えてもよい)
さて，上のように一定額を賭けるのではなく，一定率の賭け金を賭ける場合はどうなるだろうか.
そう考えて，貴方は毎回次のように賭けることにした，としよう.
# 大穴狙いに切り替わっている(^-^)
| サイコロ2個の数字合計 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 賭け金 | 所持金の 5% | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 所持金の 5% |
これならじり貧になるとしても赤字にはならない(^-^).
さて，この場合の調査もほぼ同様にして出来る．
賭け方を変えたので，まず Bet を修正し，
利益が額そのものではなく，率になったので Summation を修正して，同様に調査してみよう.
In[44]:= Bet[num_] := Module[{lst},
lst = {5,0,0,0,0,0,0,0,0,0,5};
Return[ lst[[num-1]] ]
] ← 賭け金の(所持金に対する) パーセンテージ 表示, に意味が変わっている.
In[45]:= Table[Obtain[n], {n, 2, 12}]
Out[45]= {140., -10, -10, -10, -10, -10, -10, -10, -10, -10, 140.}
← 各々，どの数字になったら所持金がどれくらいの % で増減するか確認.
例えば，「2」が出たら，140%増し，ということになる.
In[46]:= SummationPer[a_]:= Table[
Product[ 1+(a[[j]]/100.0), {j, 1, n} ], ← 1+a[j]/100 がその時点での利益の所持金比率.
{n, 1, Length[a]}
] ← 新しいリストの n 番目の要素 = (1+a[1]/100)*(1+a[2]/100)* … *(1+a[n]/100)
こうしておいて，続けて賭けてみたらどうなるか見てみよう.
In[47]:= Bets[100] ← 100回続けて賭けてみた.
Out[47]= {{-10, -10, -10, -10, -10, -10, -10, -10, -10, -10, -10, -10, -10,
…略…
6, 6, 3, 8, 6, 8, 7, 10, 10, 7, 11, 2, 9, 7, 10, 3, 5, 6, 5, 12, 6, 4, 8, 7, 8}}
← ほとんど当たらないが，時々大当たりしている個所があることがわかる.
In[48]:= SummationPer[ %47[[1]] ]
Out[48]= …略…
In[49]:= ListPlot[ %48, PlotJoined -> True]
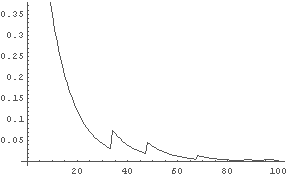← 初期所持金額に対するその時点での所持金比率の経過.
時々ピクンとはね上がっているところが，大穴が当たったとき，に相当する.
しかし，大穴が数回当たっても全体としてはじり貧だということがよく分かる(^-^).
# もちろん，勝ち上がる，ということもまれにあるはずではあるが…
さて，これは定額で賭けた時と挙動は異なるものの，やはり賭けた回数
n と所持金の間には何らかの関係があるようだ.
そこで，その関係を探ろう.
こうした直線的でないが一定の方向性があるグラフについて調べるには
対数グラフで見てみる，というのがまずは王道なので，そうしてみよう.
In[50]:= LogListPlot[ %48, PlotJoined -> True]
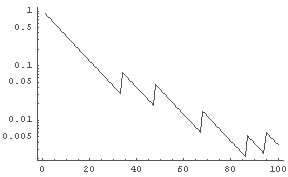← 初期所持金額に対するその時点での所持金比率の経過の対数グラフ
これを見ると，明らかに所持金と賭け回数との間にはきれいな関係があるようだ. まずわかることを箇条書きにしてみよう.
この二つのファクターを数式にかえて，次のように大胆に仮説にしてみよう.
■ 仮説 2
この賭けに対し，上記の配当率と定率賭け金のもとで n 回賭けた時の所持金を Y(n) とすると，およそ
log(Y) = βn + γn ⇔ Y = exp( βn + γn )
である.
ただし，β < 0 < γ ，かつ，γ < |β| である.
この βn という項が先の観察結果 1 に相当し，γn という項が観察結果
2 に相当する.
(授業中の課題) → 仮説 2 は正しいと言えるか，実験を繰り返して検証せよ.
(授業中の課題) → 仮説 2 が正しいとして，β の値を推定せよ.
□ レポート課題 5
仮説 2 の γ の値を推定せよ.
□ レポート課題 6
仮説 2 の β，γ の値を理論的に示せ.
□ レポート課題 7
上の賭けに対し，上記の配当率のもとでどう定率で賭けたらもっとも累積利益を大きくできるか考えよ.
(もっとも損しない，と言い換えてもよい)
さて，サイコロを 1つ増やして 3つにした場合はどうなるだろうか.
In[51]:= IRHistogram[ Table[ DiceSum[3], {1000}] ] ← サイコロ3個同時投げを 1000回やってみて，その和の確率分布をみると…
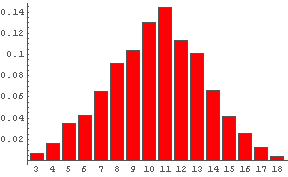
サイコロ2個投げの時同様，真ん中の値に対して確率が高い，山型の分布をすることが分かる.
2個投げの時同様，丁寧に考えれば確率分布を理論的に求めることができるはずである.
□ レポート課題 8
サイコロ3個投げの場合の確率分布を理論的に求めよ.
□ レポート課題 9
サイコロ3個投げの場合も賭けをやってみたらどうなるか，調べてみよ.
さて，ここでちょっと視点をまた変えて考えてみよう.
サイコロを 1つから 2つに増やしてみたら，平らな確率分布(頻度分布でもよい)
が山型の分布に変わった.
しかし，2つから 3つに増やしたら，山型である，という事実は変化していない.
では，3つから 4つに増やしたらどうなるだろう?
そしてさらに増やしてみたら?
それをやってみよう.
In[52]:= DiceSumHisgr[num_] := IRHistogram[ Table[ DiceSum[num], {1000} ] ]
← サイコロの数を変えて，出た数字の和の確率分布をみる関数.
1000回やってみる，としている.
In[53]:= DiceSumHisgr[4]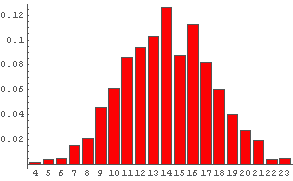 
In[54]:= DiceSumHisgr[5] 
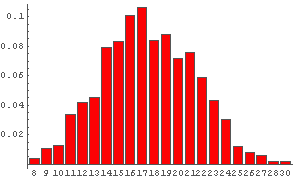In[55]:= DiceSumHisgr[8] 
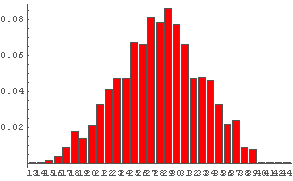In[56]:= DiceSumHisgr[10] 
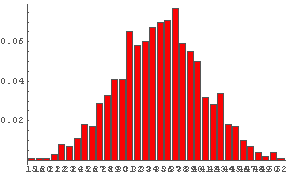In[57]:= DiceSumHisgr[20] 
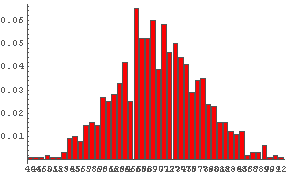In[58]:= DiceSumHisgr[40] 
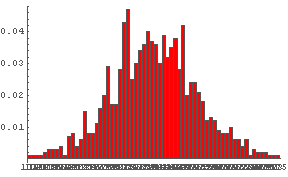In[59]:= DiceSumHisgr[60] 
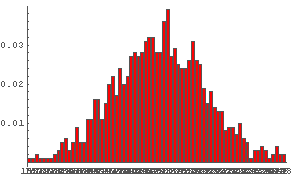In[60]:= DiceSumHisgr[80] 
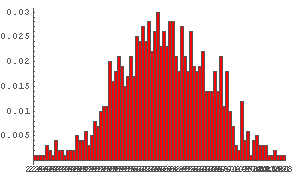In[61]:= DiceSumHisgr[100]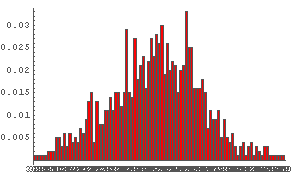 
どうだろう?
サイコロの数を増やしていっても，その出る数字の和の分布の「形」はよく似ていることがわかるだろう.
# 全く同じでないことは，理論値が計算できることから予想できるだろうが.
これをよりきちんと，かつ大胆な予想込みで言うと，次のように言えるだろう.
■ 仮説 3
サイコロを複数投げて，出た数字の和の確率分布の形状は，
サイコロの数を増やすと一定の形状に近づく.
(授業中の課題) → どんな形状に近づくのか，推測せよ.
(ヒント) 山型形状の真ん中の値や，すその幅は，単にサイコロの数に比例する.
ということは，全面積 = 1 なことから高さはその逆，つまり反比例になるだろう.
それを考慮に入れてグラフを描けば…
□ レポート課題 10
仮説 3 を理論的に示せ.
さて，ここで「ひねくれて」見よう.
上の仮説 3 はサイコロがきれい，つまり，均等な確率分布をしているから成り立つのではないか?
と疑ってみるのである.
つまり，いかさま師がつかうようなサイコロだったら仮説 3 は成り立つまい，という疑いである.
そこで，「サイコロにインチキをして，歪めて」みよう.
そこで，次のようにインチキなサイコロを作る.
| サイコロの目 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|
| 出る確率 | 1/21 | 2/21 | 3/21 | 4/21 | 5/21 | 6/21 |
これは次のようにすればよい.
In[62]:= Die[ ] := Module[{d, r},
d = Random[Integer, {1,21}];
r = Which[
d < 2, 1,
d < 4, 2,
d < 7, 3,
d < 11, 4,
d < 16, 5,
True, 6
];
Return[r]
]
In[63]:= Table[ Die[], {1000} ];
In[64]:= IRHistogram[%] ← ためしに 1000回この「ゆがんだ」サイコロを振ってみると…
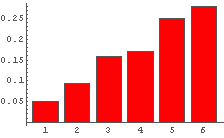← 狙い通りにゆがんでいる(^-^).
さて，このゆがんだサイコロを複数個同時に投げてその和の分布を見てみよう. 幸い，関数は何も書き換える必要がないので，すぐ実験をしてみよう.
In[65]:= Table[DiceSumHisgr[n], {n, 2, 10, 2}]
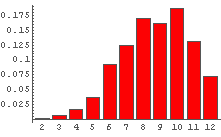
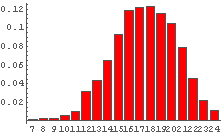
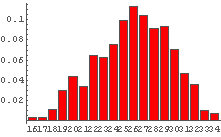
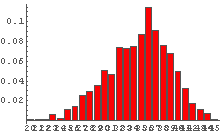
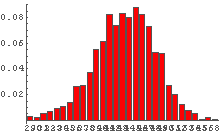In[66]:= Table[DiceSumHisgr[n], {n, 20, 100, 20}]
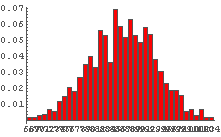
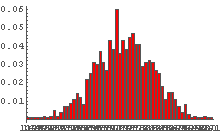
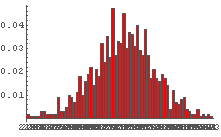
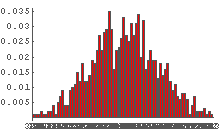
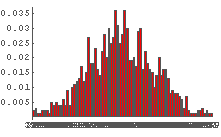
これを見てみると，サイコロの個数が少ないときはゆがみの影響が出ているものの，
サイコロの個数が増えるにつれゆがみの影響は少なくなり，
最終的にゆがんでいないときと似たような形状になっているように見える.
これは驚きである.
なぜなら，乱数発生源の性質に関わらず，それを集めると同様の性質が現れてくる，ということを示唆しているからである.
この驚きの性質を仮説としてあらわせば以下のようになるだろう.
■ 仮説 4
サイコロを複数投げて，出た数字の和の確率分布の形状は，
サイコロの数を増やすと，
サイコロ自身の確率分布が歪んでいてもその歪みに関係ない
一定の形状に近づく.
(授業中の課題) → サイコロの歪みの様子を変えてみて，仮説 4 が成り立つかどうか確かめてみよ.
実は，この仮説は「中心極限定理」と呼ばれる定理であり，
その一定形状などについてもいろいろ分かっている.
また，この定理の応用は幅広い.
社会学や生物学，医学などで多用される統計学の初歩の初歩として要求される知識，といってよいだろう.
□ レポート課題 11
「中心極限定理」について何かの本で調べ，理解し，今回の実験との関連を述べよ.