← 各々の文字列の出現頻度による円グラフ. あきらかに片寄っている. どう片寄っているか?
今回は，ランダム性についていろいろと調べてみよう.
乱数について調べる，と言い換えてもよい.
ちなみに，ランダム性について「でたらめさ」と称して前回，前々回といくつかの知見，仮説をわれわれは得ている.
もしその内容を理解し損ねた，忘れてしまったというのであれば，
もったいない話なので，一度ゆっくり読み返しておくことを勧める.
さて，ランダム性について調べることが何の役に立つのか?
そりゃいろいろと役に立つ.
もし宝くじの当選番号がランダムでなかったら? というのは置いておいて(^-^)，
ランダム性について詳しく知ることは情報理論や量子力学(とそれから繋がる哲学)や心理学へのとっかかりの一つになるのだ.
古いタイプの暗号理論にも乱数性は重要だ.
また，一見ランダムに見える現象でもランダムでない(隠れた)法則性があることが見いだせるならば，
それは科学としても現実問題としても重要な利益をもたらすだろう.
そういう意味でも，ランダム性について少しでも認識を深めておくことは重要だ.
さて，まずは最も身近な乱数生成装置の候補として「人間」を考えてみよう.
逆に言えば，人間を使って乱数を作る試みを行うことで，乱数の性質と人間の性質の両方で
直感的な理解が深まる可能性があるので，それを期待する，ということである.
一番簡単にランダム性をチェックするには，
人間が二つの記号をうまくランダムに並べることができるかどうか調べて
みればよい.
そこで，0 と 1 という二文字を使ってやってみよう.
In[1]:= a = "01000101110101001011101011010100101000101010010101100101001010001010100101010010101110101010010101001010"
← 一生懸命，ランダムになるように自分で入力してみる.
さて，こうやって人間が作ったこの並びはどこまでランダムだろうか?
いいかえると，
「ランダムさとはどうやって判断すれば良いのか? 」
という疑問である.
もちろん，これまでの授業を通じていくつかその手がかりをわれわれは得ているが，
今回はまた少し違う方向から攻めてみよう.
まず，誰でも思いつくことから調べてみよう.
■ 仮説 1
{0,1}からなる数列が真にランダムと言えるならば，0 の出現頻度と 1 の
出現頻度は等しいはずである(つまり確率で 0.5 ずつ).
この仮説はむしろランダム性の「提案」に近い性質のものであるので，
この仮説が正しいと仮定して，上の数列がこの仮説を満たすかどうかチェックしてみよう.
In[2]:= StringPosition[a, "0"] ← まず，"0" が含まれている場所をチェック.
Out[2]= {{1, 1}, {3, 3}, {4, 4}, {5, 5}, {7, 7}, {11, 11}, {13, 13}, {15, 15},
{16, 16}, {18, 18}, {22, 22}, {24, 24}, {27, 27}, {29, 29}, {31, 31},
{32, 32}, {34, 34}, {36, 36}, {37, 37}, {38, 38}, {40, 40}, {42, 42},
{44, 44}, {45, 45}, {47, 47}, {49, 49}, {52, 52}, {53, 53}, {55, 55},
{57, 57}, {58, 58}, {60, 60}, {62, 62}, {63, 63}, {64, 64}, {66, 66},
{68, 68}, {70, 70}, {71, 71}, {73, 73}, {75, 75}, {77, 77}, {78, 78},
{80, 80}, {82, 82}, {86, 86}, {88, 88}, {90, 90}, {92, 92}, {93, 93},
{95, 95}, {97, 97}, {99, 99}, {100, 100}, {102, 102}, {104, 104}}
In[3]:= Length[%]
Out[3]= 56 ← 次にリストの要素の個数を調べることで，"0" が実際に何回出てきたか調べる.
In[4]:= StringLength[a]
Out[4]= 104 ← もとの数列の数字の個数を調べる.
In[5]:= %3/%4 // N
Out[5]= 0.538462 ← 上の結果から，"0" の出現頻度を見る.
という結果が得られ，"0" の出現頻度(確率)が 0.5385 程度なので，
(⇔ "1" の出現頻度は 0.4615 程度ということでもある)
手で作ったこの数列は仮説 1 をまあ悪くない程度に満たすと言ってよいだろう.
ただし途中で
● 文字列 … 文字をつなげたもの.
→ "ddef" など，" で囲って作る.
変数 a に代入するには a = "ddef" などとする.
● 文字列の含まれる場所を調べる … StringPosition[文字列1, 文字列2]
→ 文字列2 が文字列1 のどこに含まれるのか，含まれる文字列の
{最初の位置,最後の位置} のリストを与える.
● 文字列の文字数 … StringLength[文字列]
→ StringLength["abc"] は 3 となる.
を用いている.
(授業中の課題)
→ 自分で同じようにやってみよ.
さて，ではこれで上の列はランダムだと言ってよいだろうか.
いや，それではあまりに不完全だろう.
例えば，仮説 1 を満たすだけでよいのならば，
010101010101010101010101010101010101010101010101
という「0 と 1 を交互に並べた規則正しい列」もランダムだということになってしまう.
つまり，仮説 1 だけではランダム性を述べるには不十分だということである.
そこで，仮説 1 を少し複雑にしたものを次のように考えてみる.
■ 仮説 2
{0,1} からなる数列が真にランダムと言えるならば，"00", "01", "10", "11"
の出現頻度は等しいはずである(つまり確率で 0.25 ずつ).
これは続きの二文字を見ると上のように 4つの場合わけができるが，ランダムならば
"0" と "1" は平等だから，結果としてその 4つの組み合わせも平等であり，
その出現確率も平等であるべきだ，という考えである．
よく考えれば，これはまあ最もな仮説と言えよう.
ではこの仮説 2 を上の数列は満たすのかを調べてみよう.
In[6]:= Length[StringPosition[a, "00"]] ← "00" がいくつ含まれるか.
Out[6]= 15
In[7]:= StringLength[a] - 1 ← "xx" という続きの二文字は a の中に「a の文字の個数 -1」だけありうる.
Out[7]= 103
In[8]:= %6/%7 //N ← "00" の出現頻度.
Out[8]= 0.145631
おや? "00" の出現頻度が 0.25 から大きくハズレているようだ. あと三つの組み合わせ "01", "10", "11" についても調べてみよう. 毎回これまでの入力をするのが面倒なので，その文字列の出現頻度を出力する関数にしてしまおう.
In[9]:= Rate[whole_, str_] := Module[{num, lwhole, lstr},
lstr = StringLength[str];
lwhole = StringLength[whole];
num = Length[StringPosition[whole, str]];
Return[num/(lwhole - lstr + 1) // N]; ← "xx..." という n文字続きのパターンは全部で lwhole - lstr + 1 だけありうるので.
]
In[10]:= Rate[a, "00"]
Out[10]= 0.145631 ← 文字列 "00" の出現頻度.
In[11]:= Rate[a, "01"]
Out[11]= 0.38835 ← 文字列 "01" の出現頻度.
In[12]:= Rate[a, "10"]
Out[12]= 0.38835 ← 文字列 "10" の出現頻度.
In[13]:= Rate[a, "11"]
Out[13]= 0.0776699 ← 文字列 "11" の出現頻度.
どうやら，この結果を見ると上に作った数列は仮説 2 から大きくハズレるようである.
(授業中の課題)→ グラフではっきり見てみればより分かるので，適当なグラフで見てみよう.
つまり，仮説 2 を信ずるのであれば，上の数列は「ランダムではない」
ということだ.
では，仮に仮説 2 を満たしているならば上の数列はランダムであろうか?
いや，やはり同様に不足があるだろう.
つまり，仮説 1 → 仮説 2 と発展したように，さらに発展した仮説が考えられるのである.
■ 仮説 3
{0,1} からなる数列が真にランダムと言えるならば，"000", "001", "010", "011"
"100", "101", "110", "111"
の出現頻度は等しいはずである(つまり確率で 0.125 ずつ).
これも一応，上の数列にたいしてチェックしておこう.
ただ，この 8通りの文字列を手で入力するのは面倒なので，これらを自動で作ってくれる関数を用意すべく
Mathematica と格闘してみよう.
# 8 通りぐらいならまだ良いが，4 文字になると 16 通り，その次は 32 通りとどんどん増えるので今のうちに…
In[14]:= Table[{"0", "1"}, {3}] ← 8通りの組み合わせを作らせてみよう. まず，こうして…
Out[14]= {{"0", "1"}, {"0", "1"}, {"0", "1"}}
In[15]:= Distribute[%, List] ← こうすると 8 通りの組み合わせができる.
Out[15]= {{"0", "0", "0"}, {"0", "0", "1"}, {"0", "1", "0"}, {"0", "1", "1"},
{"1", "0", "0"}, {"1", "0", "1"}, {"1", "1", "0"}, {"1", "1", "1"}}
In[16]:= Map[StringJoin, %] ← あとは文字列としてまとめれば OK.
Out[16]= {"000", "001", "010", "011", "100", "101", "110", "111"}
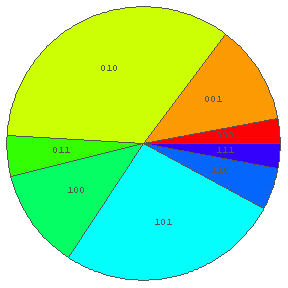
In[17]:= {Map[ Rate[a, #]& , %], %} ← 各々の文字列の出現頻度.
あとのグラフのために，各々の文字列ももう一回出力しておく.
Out[17]= {{0.0294118, 0.117647, 0.343137, 0.0490196, 0.117647, 0.264706, 0.0490196, 0.0294118},
{"000", "001", "010", "011", "100", "101", "110", "111"}}
In[18]:= Needs["Graphics`"]
In[19]:= PieChart[%17[[1]], PieLabels -> %17[[2]] ]
← 各々の文字列の出現頻度による円グラフ. あきらかに片寄っている. どう片寄っているか?
□ レポート課題 1
上の出現頻度の偏りはどうして生ずるか.
キーを打つ人の「心理」を良く考えて意見を述べよ.
ただし途中で
● 関数の引数の全ての組み合わせを用意して関数を分配する … Distribute[関数[引数], 分配記号]
→ Distribute[f[a+b, c+d], Plus] とすると，分配記号 は Plus すなわち + になるので，
+ で引数を分離して，全ての組み合わせ [a,c] [a,d] [b,c] [b,d]
を引数として，関数 f に対し + で分配されて
f[a,c] + f[a,d] + f[b,c] + f[b,d] となる.
→ だから，Distribute[{{0,1}, {0,1}, {0,1}}, List] とすると
{{0,0,0}, {0,0,1}, {0,1,0}, {0,1,1}, {1,0,0}, {1,0,1}, {1,1,0}, {1,1,1}}
の全ての場合わけが得られる.
→ よく分からない人は，この応用を覚えるだけでもよいだろう.
●文字列をつなげる … StringJoin[文字列1, 文字列2,...]
→ 特に説明は要らないだろう(^-^).
● 円グラフを描く … PieChart[リスト]
→ リストの値に応じて角度を比例した大きさで割り振る.
時計の 3時方向から反時計回り.
→ Needs["Graphics`"] が事前に必要である.
→ ● 図に説明を入れる … オプション PieLabels
: 値のリストに応じた文字列のリストを指定すれば良い.
を用いている.
さて，ここまで来ると，この仮説の連携はいくらでも続きそうだということは予想できるだろう.
そこで，さらにこの論理を押し進めれば，大胆に次のような仮説でまとめることができるのではないだろうか.
■ 仮説 4
{0,1} からなる数列が真にランダムと言えるならば，
n 個(1≦n)の文字からなる文字列(2n 個の組み合わせ) "0...00", "0...01", ... "1...11"
の出現頻度は等しいはずである(つまり確率で (1/2)n).
これはつまり，
「ランダムな数列とは理論的に平等な部分数列の出現確率が等しいものをいう」
と言っているようなものだ.
これはランダム性の中身に近づくまた一つの手がかりである.
□ レポート課題 2
仮説 4 が成り立つならば，その数列はランダムであるといえるだろうか?
実験などを通じて自分なりの考えを示せ.
そこで，上にやったことを単純にまとめる関数を作って，
気楽に実験できる環境を用意しよう.
In[20]:= BinComb[num_] := ← num 個の {0,1} からなる文字列を全て出力する.
Map[StringJoin,
Distribute[Table[{"0","1"}, {num}], List]
]
In[21]:= BinRate[whole_, num_] := Module[{bcomb},
bcomb = BinComb[num];
Return[{Map[Rate[whole, #] &, bcomb], bcomb}]
] ← num 個の {0,1} からなる文字列の各々の出現頻度を出力.
In[22]:= BinRPie[whole_, num_] := Module[{brate},
brate = BinRate[whole, num];
PieChart[brate[[1]], PieLabels -> brate[[2]] ];
] ← num 個の {0,1} からなる文字列の各々の出現頻度による円グラフを出力.
In[23]:= BinRPie[a, 4] ← ためしに 4個文字からなる文字列の各々の出現頻度による円グラフを出力すると…
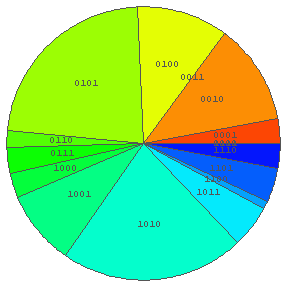← これもあきらかに片寄っている. どう片寄っているか?
(授業中の課題) → 円グラフが片寄らないような数列を自分で入力してみよ.
できるだろうか?
では，ここで理想に近い乱数列だとどうなるか一目見ておこう(詳しくはまた後でやる). それには，Mathematica 自身がもつ乱数生成機能を使ってみる. ただし，上にせっかく作った BinRPie とかの便利な関数を使うために， リスト → 文字列 と変換する ListToString[リスト] という関数を先に用意しておこう.
In[24]:= ListToString[a_] := Apply[StringJoin, Map[ToString, a]]; ← リストを入れると，文字列に変換する.
In[25]:= ListToString[{0, 2, 3, 1, d, 5}] ← ためしにこうやってみると，
Out[25]= 0231d5 ← 確かに文字列になっている.
ただし，
● 文字列に変換する … ToString[引数]
→ 引数を "" で囲むだけ… のような気がするが(^-^),
オプションを使い分けて表示形式を自由に設定できるのがその真髄，らしい.
を用いている.
さて，これを用いて，{0, 1} を Mathematica の能力でランダムに混ぜてたくさん出力させてみよう.
それには次のような関数を作れば良い.
In[26]:= RandomList[ite_] := ListToString[Table[Random[Integer], {n, 1, ite}]]
← {0,1} による指定した長さのランダムな文字列を作る.
In[27]:= RandomList[200] ← 試しに，長さ 200のランダムな文字列を作らせてみる.
Out[27]= 00100111110000000010100010100110101011001001010000110011011101110110101000011
10110011001010000010111101011000010010100000011100110010011001101100111010110
1110100000101111010010110000100100101001110000
ただし，途中で
● (疑似)乱数を与える … Random[タイプ, 範囲]
→ タイプは，Integer, Real, Complex の三種類.
→ 範囲は {min, max} の形で与える.
→ タイプが Real の場合のみ，Random[Real, 範囲, n] として，精度 n 桁にするオプションがある.
→ 引数を省略すると，次のようになる.
Random[] ⇔ Random[Real, {0,1}]
Random[Integer] ⇔ Random[Integer, {0,1}]
Random[Complex] ⇔ Random[Complex, {0,1+i}]
を使っている.
さて，Mathematica に作らせた(ほぼ完全な?)ランダムな文字列に対して，上でやったようなのと同様の解析をしてみよう.
In[28]:= BinRPie[%27, 1]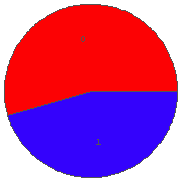 
In[29]:= BinRPie[%27, 2] 
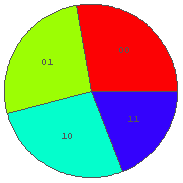In[30]:= BinRPie[%27, 3] 
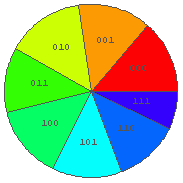In[31]:= BinRPie[%27, 4]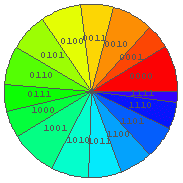 
どうだろう?
自分の手で入力した，つまり人間がランダムにしようとして作った文字列と比べて，どうだろうか?
また，今までたてた仮説に対してはどうだろうか?
BinRPie[%27, 5] などと(チェックする)文字列の長さを変えるなどして比較検討してみるべし.
□ レポート課題 3
ここで作った関数 BinRPie, RandomList などを用いて，
仮説 4 が正しいかどうか調べよ.
(Mathematica の Random 関数を信用するという前提のもとで，ということになる)
さて，Mathematica に作らせたランダムな文字列との比較も考えると，
人間の作る文字列は片寄っていて，ランダムとは言えそうにないことが明らかである.
では，人間はどういう風に片寄っているのか，検討してみよう.
まず，上の人間が作った文字列に対する出現頻度の円グラフをじっと眺めると，
次のことが言えそうだ.
これを言い換えて仮説としてみると，
■ 仮説 5
人間はランダムな文字列を作ろうとしても，
「同一文字が続くのを避け，交互に並ぶようにしようとする傾向がある」らしい.
これは，自分で文字列をでたらめにしようとして入力するときのことをゆっくり思い出せばかなり納得できるであろう.
ちなみに，これは「ランダムさ」を調べる過程で心理学的な知見を得た
と言える.
つまり，数学は心理学にとって非常に基礎的で重要な役割を成す一例，といえよう.
さて，上の仮説 5 では解析はまだ不十分である.
そこで，仮説 5 で提唱する「傾向」がどれくらい強いのか，定量的に調べてみよう.
それには，その「傾向」をより数学的に書き直してみて，Mathematica で調べてみればよい.
つまり，仮説 5 は次のように言い換えられると考えるのである.
■ 仮説 6
人間は {0,1} によるランダムな文字列を作ろうとするとき，
「ある文字に続けて，
確率 r で同一文字を，
確率 (1-r) で違う文字を選ぶ」.
ただし，r < 0.5 である.
さて，これなら Mathematica で実験して確かめることができよう.
つまり，仮説 6 に従って文字列を作るような関数を作り，
人間が実際に作った文字列と比較してみればよいのである.
そこで，次のような仮説 6 に従う「人間モドキ」乱数生成関数を用意する.
In[32]:= HumanR[before_, r_] := Module[{rnd, result},
rnd = Random[];
result = If[ rnd < r, before, 1 - before];
Return[result];
]
← 数 0 or 1 を入力するものとして，
確率 r で前の数(before)を出力，確率 (1-r) で逆の数(1-before)を出力.
In[33]:= HumanR[0, 0.3] ← 試しに，確率 r=0.3 として 0 を入力すると,
Ount[33]= 1 ← 確率 0.3 で 0 が，0.7 で 1 が出力される.
In[34]:= NestList[ HumanR[#, 0.3]&, 0, 100]
← 0 からスタートして，確率 0.3 で同じ文字，確率 0.7 で違う文字を 100 個まで出力させてみる.
Oun[34]= {0, 1, 1, 0, 0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1,
1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 1, 0, 0, 1, 1, 0, 1, 0, 0,
0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1,
0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 1, 0, 0}
In[35]:= HumanRList[r_, ini_, ite_] := ListToString[NestList[HumanR[#, r] &, ini, ite]]
← それをまとめて，最後に文字列に直すようにして関数とする.
In[36]:= HumanRList[0.3, 0, 100] ← ためしにやってみると…
Out[36]= 01001011011011001011010111010101010110101000101001100100100011101001101110010
101101101101010101010001
これで道具立てはできた.
ただし途中で
● 関数を引数に繰り返して適用した結果を並べる … NestList[関数, 引数, 適用回数]
→ 例えば，NestList[f,x,5] は
{x, f[x], f[f[x]], f[f[f[x]]], f[f[f[f[x]]]], f[f[f[f[f[x]]]]]}
となる.
→ 実はすご〜〜く便利な関数.
であるからこれまで紹介しなかった(^-^).
を用いている.
さて，では早速調べてみよう.
まず，r = 0.1 とでもして，人間の場合と比較してみよう.
In[37]:= HumanRList[0.1, 0, 200] ← r=0.1, 長さ 200 としている. 初期値は 0 でも 1 でもいいだろう.
Out[37]= 00010110101010101010101101001010101010101010100101010100101010110100101101010
100010101010101010101010101010101010101001101010101010101010110101010101010100
1001010101010101010101011101010101010110101010
In[38]:= BinRPie[%37, 1]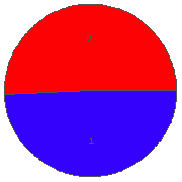 
In[39]:= BinRPie[%37, 2] 
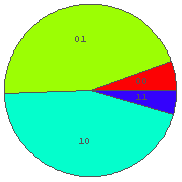In[40]:= BinRPie[%37, 3] 
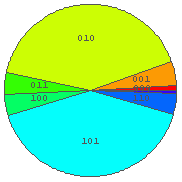In[41]:= BinRPie[%37, 4]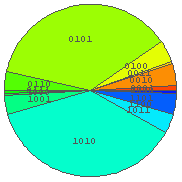 
… ちょっと偏りすぎか. r = 0.1 は小さすぎたようである.
(授業中の課題)→ r = 0.2, 0,3, 0.4 あたりをやってみる!
□ レポート課題 4
仮説 6 の r はいくつぐらいが妥当といえるか.
だいたいの精度でよいので調べてみよ.
蛇足…
実は，こうした乱数列を人間に作らせる心理実験は数多くなされ，研究されている.
これまでに，次のような傾向が報告されているらしい.
(Cf. "無限へチャレンジしよう", Clifford A. Pickover 著,
一松 信 訳, 森北出版, ISBN4-627-01890-8, p.282.)
さて，仮説 6 が正しいとすると，人間が {0,1} で作ったランダムな文字列には "01010101…" という要素がかなりの確率で現れることになる. これの極端なものををグラフにすると，
In[42]:= Flatten[Table[{0, 1}, {n, 1, 20}]]
Out[42]= {0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1,0,1}
In[43]:= ListPlot[%, PlotJoined -> True]
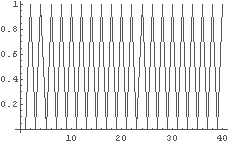
ということだから，グラフで見ると，最も刻み幅の小さい波で構成されて
いる ⇔ 周波数の最も高い波「だけ」で構成されている，ということになる.
実際には, 01010… 以外の要素も混ざってくるので，それを勘案すると，
仮説 5 は次のように言い換えられる，ということである.
■ 仮説 7
人間が {0,1} によるランダムな文字列を作ろうとして得るものを「波形」
としてとらえると，周波数の高い波の成分が多い.
→ 「ランダム ⇔ 周波数成分の均一性」 として考えた，
授業第 11 回の仮説 2 との関連をよく考えよ.
周波数成分を見るには，Fourier 展開を使う，というのが定石であるから，
{0, 1} による文字列を波形としてみて Fourier 展開し，
グラフにするような関数を作り，それで調べてみよう.
それにはまず 文字列→リスト に直す関数が必要なので，先にそれを作る.
In[44]:= StringToList[a_] := Map[ToExpression,
Table[StringTake[a, {n}], {n, 1, StringLength[a]}]
]
In[45]:= StringToList["0100101010010101"] ← 試しにやってみると…
Out[45]= {0, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 1, 0, 1, 0, 1}
ただし途中で
● 文字列の一部分を取り出す … StringTake[文字列,範囲]
→ 範囲の指定は通常は {min, max} だが，他の形もあるので，詳しくは ?StringTake としてヘルプを見ておくこと.
→ ちなみに，StringTake{文字列, {m}} とすると，文字列の第 m 番目の文字が得られる.
● 数字，数式に変換する … ToExpression[文字(列)]
→ 引数が "" で囲まれている場合，その "" をはずす，と思えばよい.
→ ToExpression["101"] は 101 という数字になる.
を用いている.
で，これを用いて，{0,1} からなる文字列を波形として見て, その
離散 Fourier 変換をグラフにする関数を作る.
In[46]:= ListToFourier[a_] := Module[{lst},
lst = StringToList[a]; ← まずリストに直す.
ListPlot[
Take[
Abs[Fourier[lst]],
Quotient[Length[lst], 2] ← 周波数域の半分が意味のあるデータなので.
] ,
PlotJoined -> True]
]
この関数を用いて，{0,1} からなる文字列として先に作った
に対しては以下のようになる.
In[47]:= ListToFourier[a]
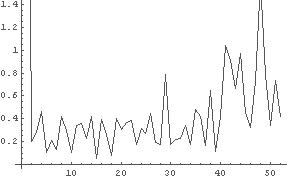← 人間が手で入力したもの
In[48]:= ListToFourier[%27]
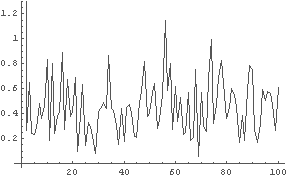← Random 関数で作ったほぼ完全にランダムと思われるもの
In[49]:= ListToFourier[%37]
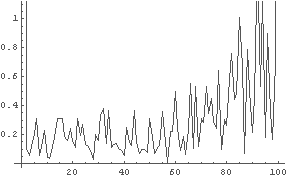← r = 0.1 として仮説 6 に基づいて作ったもの
せっかくなので，他にもいくつか適当な文字列を作って，解析を行ってみよう.
果たして仮説 7 は正しいだろうか.
→(授業中の課題)
□ レポート課題 5
仮説 4, 仮説 6, 仮説 7 の関連性について考察せよ.