さて,まずは先週の続きである.
先週定義した Norm[], InnerProduct[] を用いるので,先週の該当部分
を Mathematica に入力し,Mathematica に教えておくこと.
FT[x, 10] の結果(先週の Out[31]) を見ると,
x ≒ 2 sin(x) - sin(2x) + 2/3 sin(3x) - 1/2 sin(4x) + 2/5 sin(5x)
- 1/3 sin(6x) + 2/7 sin(7x) - 1/4 sin(8x) + 2/9 sin(9x) - 1/5 sin(10x)
となっていて,sin(kx) の係数にどうも規則性が有りそうに見える.
つまり,sin(kx) の係数 = (-1)k+1 2/k となりそうだ.
これをきちんと言うと,
■ 仮説1 x の(狭義)Fourier 展開は次の式になる.
n 2
x = lim Σ (-1)(k+1) --- sin(kx)
n→∞ k=1 k
これを確認してみようとすると,
● 和 … Sum[関数,変数の範囲]
→ 例えば,12 + 22 + 32 + 42 + ... + 502 なんかは…
In[1]:= Sum[n^2, {n, 1, 50}]
Out[1]= 42925
を用いて,
In[1]:= Fx[n_, x_] := Sum[(-1)^(k + 1) 2/k Sin[k x], {k, 1, n}]
← 仮説の右辺を Fx(n,x) と書いている.
In[2]:= Nn[n_] := Norm[Fx[n, x] - x] // N ← 仮説の 右辺 - 左辺 のノルムを計算してみる.
ノルム[g] = 0 ⇔ g = 0 を利用している.
In[3]:= Table[Nn[n], {n, 1, 30}] ← 仮説の 右辺 - 左辺 のノルムを n=30 まで計算して並べてみる(時間がかかる…)
In[4]:= ListPlot[%3, PlotJoined -> True, PlotRange -> {0, 3}]
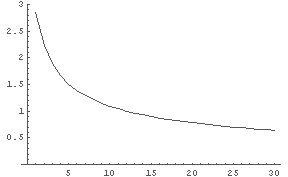 ← まあ 0 に近づいているようにも見える
← まあ 0 に近づいているようにも見える
より,それなりに納得できそうだ.
ノルムではなくて,関数の形そのものを書いて納得してみるのもいいだろう.
→ 授業中の課題
さらに,
● パッケージの読み込み … Needs["パッケージ名"]
→ どんなパッケージがあるか,いつ必要なのかはマニュアルを見れば書いてあるので,必要になるまで意識しなくて良い.
他に,<< パッケージ名 という方法もある.
詳しくは挙動が違うらしいが,まあ好きな方でよいのではないか.
● 特殊なグラフィック関数を使えるように準備する … Needs["Graphics`"]
→ 最後の ` (バッククォート) を忘れる,間違える,というのをよくやるので注意.
● データのグラフを両対数で描く
… LogLogListPlot[リスト]
→ 上の Graphics パッケージ読み込み,をしておかないと使えないので注意.
を用いて,上のグラフを両対数グラフとして描いてみよう.
これは,「変化が次第にゆっくりになるようなグラフ」の挙動の本質を掴むのによく使う手法であるので,覚えておくとよい.
In[5]:= Needs["Graphics`"]
In[6]:= LogLogListPlot[%3, PlotJoined -> True]
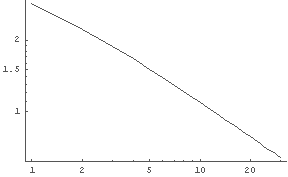 ← ほぼ直線に見える.
← ほぼ直線に見える.
これは,n → ∞ で Nn[n] → 0 となることを示唆している.
つまり,Fx[n, x] → x となる,ということだ.
Mathematica のグラフで簡単に納得するならこの程度だろう.
□ レポート課題 1
上の仮説 1 を数学的に証明せよ.
→ 部分積分を思い出せ! 思い出せなければ,web で検索だ!
さて,では x2 はどうなのか? FT[x^2, 10] とやってみると,
x^2 ≒ π^2/3 - 4 Cos[x] + Cos[2x] - 4/9 Cos[3x] + 1/4 Cos[4x] - 4/25 Cos[5x]
+ 1/9 Cos[6x] - 4/49 Cos[7x] + 1/16 Cos[8x] - 4/81 Cos[9x] + 1/25 Cos[10x]
となるので,これも最初の項を除けば簡単なルールが見つかる.
■ 仮説2 x2 の(狭義)Fourier 展開は次の式になる.
π2 n 4
x2 = --- + lim Σ (-1)k --- cos(kx)
3 n→∞ k=1 k2
□ レポート課題 2
上の仮説2 に対し,仮説1 の時同様の解析を Mathematica で行ってみよ.
さらに数学的に証明できればなおよい.
□ レポート課題 3
x3 に対して同様の仮説をたて,解析を行え.
また,数学的に証明できればなおよいのも同様.
□ レポート課題 4
x に対する Fourier展開の式(仮説1) と x2 に対するもの(仮説2)
との関係について調べよ.
Fourier 展開の応用
Fourier 展開の神髄が未知の関数を既知の関数で表すことにあることは既に学習した.
では,その現実的な「ありがたみ」は一体どのようなものなのだろうか.
具体的な例で実感してみるとしよう.
● データをファイルから入力 … Import["ファイル名", "データ形式"]
→ ファイル名の拡張子からデータ形式が正しく推測できるときは,Import["ファイル名"] だけでもよい.
を用いて,とある音声データをデータとして入力する.
このとき,次のちょっとした Tips を使っているので覚えておくと便利.
● 表示せずに実行(実行時間の節約) … 式の最後に ; (セミコロン)をつける
→ 大きめのデータを使うときなんかはとりあえずつけとけ.全然違う.
これは式を区切る,という機能の副作用である.
In[1]:= a = Import["tones1.wav"]; ← wav ファイルは拡張子から正しく推測できる.
In[2]:= b = a[[1,1]]; ← 音声データオブジェクトは
その 1,1 成分が音の大きさが並んだリストになっている.
In[3]:= ListPlot[Take[b,25000], PlotJoined -> True ];
← 最初の 25000 個を表示している
(全部で 1秒分になるように残りは私がゼロを埋めてある).
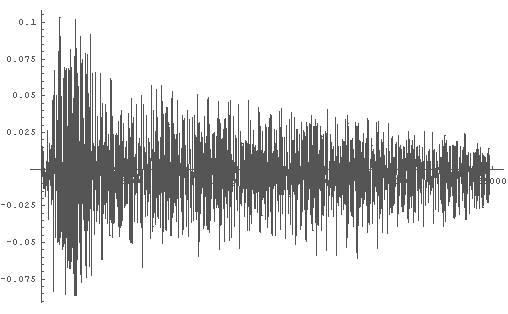
↑ 音を(サンプリングレート 44100 Hz で)取り込んで表示したもの,
ということになる.
これを見てもあまり音の性質はわからない.
なお途中で次の命令を使っている.
● それは Mathematica では何なのか? … InputForm[なにか]
→ 音声データオブジェクトの形式を調べるのに用いた.結構便利.
● リストの一部分を取り出す … Take[リスト,範囲]
さて,何かする前にきちんと取り込めたかどうか耳で確認しよう.
● リストを音として鳴らす … ListPlay[リスト,SampleRate -> サンプリングレート]
→ サンプリングレートを指定するのを忘れると音の高さが変わる(^-^;)
In[4]:= ListPlay[b, SampleRate -> 44100];
 ← どうやらピアノの音のようだ.
← どうやらピアノの音のようだ.
さて,このデータに対して Fourier 展開を行ってみたらどうなるだろう?
このデータは関数ではなくてリストなので,Fourier 展開そのものではなく,
離散 Fourier 変換(展開) を行う必要がある.
そのためのコマンドが Mathematica には既にある.
● 離散 Fourier 変換を行う … Fourier[リスト]
→ 答えも複素数のリストになる.
M 秒のデータをこの離散 Fourier 変換にかけると,
答えの第 k 成分は周波数 k/M の振動成分の大きさ,に相当する.
念の為に数式で示しておくと,この離散 Fourier 変換は
{us} → {vk} を行うとして
1 n
vk = ----- Σ us e2πi(s-1)(k-1)/n
√n s=1
と表される(n はデータの個数).
これは(定数倍を除いて)幅 M の領域での(狭義の)Fourier展開をそのまま離散化したものに相当する.
(周波数が変わるのは幅の影響)
□ レポート課題 5
(狭義の)Fourier 展開を離散化するとこの離散化 Fourier 変換になることを示せ.
→ ただし,複素数の指数関数と三角関数の関係を知らないときついか…
さて,この音声データにこの離散 Fourier 変換をしてみよう.
途中で
● 絶対値 … Abs[数]
→ 数は実数か複素数.
を使っている.
In[5]:= c = Abs[Fourier[b]]; ← 絶対値に直さないと「大きさ」にならない.
複素数を知らない人は,う〜ん…
In[6]:= a1 = ListPlot[Take[c, 1200], PlotJoined -> True, PlotRange -> {0, 0.2}];
← あまり高い周波数は実は意味がないので.
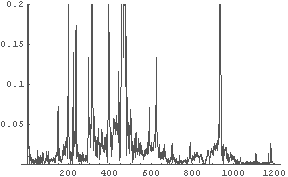 ← このグラフは何を意味するか?
← このグラフは何を意味するか?
よく考えると,このグラフは 横軸が周波数,縦軸がその周波数の音の大きさ,を表す.
つまり,離散 Fourier 変換が音声データを「周波数毎に分解」
したのである.
(注)入力した音声データの長さは 1秒ちょうどに作ってあるので,上のグラフの横軸の数字は周波数そのものであることに注意.
つまり,このグラフを見れば,「どの高さの音が鳴っているか」が基本的にわかるのである.
ピアノで言えば,どの鍵盤を押しているか,が推測できる,ということになる.
では,上のグラフからどの音が鳴っているか推測してみよう.
グラフから値を読み取る方法を用いて,だいたい,
935, 624, 468, 390 Hz
などの高さの音が鳴っていることがわかる(他にもよく見るとたくさんある).
で,音に関しては以前示したように
- 中央の「ラ(A)」の音はだいたい 440Hz.
- 音が「半音」上がると周波数は 21/12 倍になる.
という基本事実(平均律)から,音の高さと周波数の関係はわかるだろう.
あえて表にしてみればつぎのようになる.
| 音 |
C(ド) |
Cis(ド♯) |
D(レ) |
Es(ミ♭) |
E(ミ) |
F(ファ) |
Fis(ファ♯) |
G(ソ) |
Aes(ラ♭) |
A(ラ) |
B(シ♭) |
H(シ) |
| 振動数(Hz) |
261.63 |
277.18 |
293.66 |
311.13 |
329.63 |
349.23 |
369.99 |
392.00 |
415.30 |
440 |
466.16 |
493.88 |
| (1オクターブ上) |
523.25 |
554.37 |
587.33 |
622.25 |
659.26 |
698.46 |
739.99 |
783.99 |
830.61 |
880 |
932.33 |
987.77 |
この表を用いて,上の鳴っていた音の高さを見ると,
2B(上のシ♭),
2Es(上のミ♭),
B(シ♭),
G(ソ)
などの音が鳴っていたことになる.
つまり,データを「計算するだけで譜面がわかることになる」.
実はこの時鳴らしていた音は,楽譜によると
2B(上のシ♭),
2G(上のソ)
2Es(上のミ♭),
B(シ♭)
⇔
932.3, 784.0, 622.3, 466.2 Hz
だということがわかっている.
この音がどこに相当するか,グラフに重ねてみよう.
In[7]:= d = {{466.2, 0.1}, {622.3, 0.1}, {784.0, 0.1}, {932.3, 0.1}}
In[8]:= a2 = ListPlot[d, PlotStyle -> {Hue[0], PointSize[0.02]}];
In[9]:= Show[a1, a2, PlotRange -> {0, 0.2}]
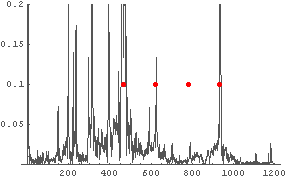 ← 赤い点が「楽譜上の音」を示す.
← 赤い点が「楽譜上の音」を示す.
ここで,いくつかのグラフを重ねるために
● オブジェクトの表示 … Show[オブジェクト(複数可)]
→ グラフィックオブジェクトを使えばグラフの重ね描きができる.
→ サウンドオブジェクトを使うと,音の再生になる.
→ 実は,複数の Plot を重ね書きするのには,DisplayTogether という関数も使える.
こちらの方がより直感的に使えるだろう.
(ただし,この関数は Graphics パッケージに入っているので,事前に
Needs["Graphics`"] を実行する必要がある)
を使っている.
□ レポート課題 6
適当な音声ファイルを用意して,同様の解析を行え.
2001.11.24 11:56:00 に沖縄県平良市狩俣周辺で起きた地震(M5.2)のゆれについても同様に解析してみよう.
こうしたデータは
強震ネットワーク(K-NET)
で入手できる.
今回はここに御世話になった.
In[10]:= data = Import["data.txt", "List"]; ← データがリスト形式の場合,
形式を明示的に指定する必要がある.
In[11]:= ListPlot[data, PlotRange -> All, PlotJoined -> True];
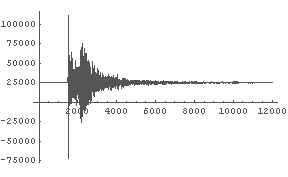 ← インパクトが一瞬あって,しばらくして大きめの揺れが来ている.
← インパクトが一瞬あって,しばらくして大きめの揺れが来ている.
データ数は 12000点で,サンプリングレートは 100Hz.
よってデータは 120秒間分,ということなので周波数を正しく合わせるには
In[12]:= fdata = Abs[Fourier[data]];
In[13]:= gdata = Table[{n/120, fdata[[n]]}, {n, 1, 11999}];
← こうして,周波数を正しく合わせておく.
In[14]:= ListPlot[Take[gdata, 6000], PlotJoined -> True, PlotRange -> {0, 20000}]
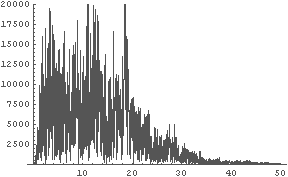 ← 非常に周波数が低いことに注目.
← 非常に周波数が低いことに注目.
人間の聞き取れる音は 20 〜 20,000 Hz 程度と言われているので,
これぐらい周波数が低いと音としてはぎりぎり聞こえるかどうか.
聞こえるような聞こえないような,という音はかえって気持悪いかも.
□ レポート課題 7
何か適当な解析対象を探して,自分で解析して寸評を加えよ.
>> 目次
 ← まあ 0 に近づいているようにも見える
← まあ 0 に近づいているようにも見える
 ← ほぼ直線に見える.
← ほぼ直線に見える.
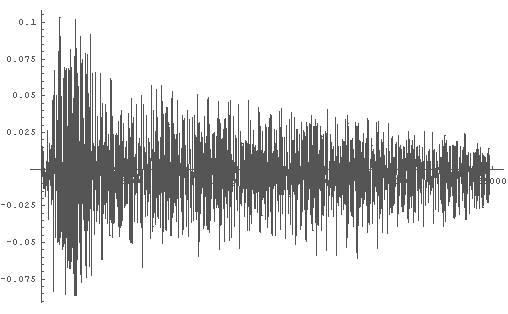
 ← どうやらピアノの音のようだ.
← どうやらピアノの音のようだ.
 ← このグラフは何を意味するか?
← このグラフは何を意味するか?
 ← 赤い点が「楽譜上の音」を示す.
← 赤い点が「楽譜上の音」を示す.
 ← インパクトが一瞬あって,しばらくして大きめの揺れが来ている.
← インパクトが一瞬あって,しばらくして大きめの揺れが来ている.
 ← 非常に周波数が低いことに注目.
← 非常に周波数が低いことに注目.