関数には無数のバリエーションがあるため，当然だが全てを「事前に列挙してチェックしておくことはできない」．
よって，知らない関数が目の前に現れたときにはその性質を知るために様々な技法を駆使する必要がある．
その最も単純な方法はこれまでに学習した「グラフを描いてみる」
というものだが，もちろんそれだけではあまりに力不足である．
そこで，既に知っている関数に分解して考える，
というフーリエ展開について簡単に学習しよう．
→本講義では時間の制約上あまり精密な議論は行わない．
詳しく知りたいものは成書をあたること．
以降(話を簡単にするために)，空間変数 x が [-π , π] の範囲にあるとする．
→ x ∈ [-L, L] としたければ，
xnew ∈ [-L, L], xold ∈ [-π, π] と考えて
xold = xnew * (π/L) とすればよい．
つまり，下に出てくる話の中のπと x を π→L, x → x * π/L と置き換えればよい．
■ 内積 x ∈ [-π, π] における二つの関数 f, g の内積を次のように定義する．
π
(f, g) = ∫ { f(x) g(x) }dx
-π
→ そもそも内積とは，おおざっぱには 演算(何か複雑なもの A, 何か複雑なもの B) = 実数
となる演算を言う．
この場合の複雑なものとは，x ∈ [-π, π] での関数，ということになる．
→ さらに言うならば内積とは，
内積 = (A の大きさ) * (B の大きさ) * (A と B の関連度)
と考えて A と B の関係性を数値で表すための一つの指標にしよう，
と目論むもの，と言ってもよい．
例えば，sin(x) と sin(x/2) の(この定義での)内積，1 と x2 の内積は各々
● 積分 … Integrate[関数，変数の範囲]
→ Plot や Play と使い方はそっくりである．
を用いて，次のように計算できる．
In[1]:= InnerProduct[f_, g_] := Integrate[f * g, {x, -Pi, Pi}]
In[2]:= InnerProduct[ Sin[x], Sin[x/2] ]
Out[2]= 8/3
In[3]:= InnerProduct[1, x^2]
Out[3]= 2π^3/3
■ (内積に基づく) ノルム … 関数の「大きさ」
関数 f(x) のノルム |f| とは，f 同士の内積 (f,f) の平方根 √(f,f) をいう．
→ 要するに，関数 f の「大きさ」である．
このためには自分同士の内積 ≧ 0 でないといけない．
(こうして数学の教科書は複雑になっていくのだ(^-^))
こうすると，
関数 f と g の関連度 = (f, g)/(|f| |g|)
と考えられることに注目しておこう．
さて，後々のためにノルムも Mathematica の関数として定義しておこう．
In[4]:= Norm[f_] := (InnerProduct[f, f])^(1/2)
← 既にある Nor という演算子に似ているので注意されるが無視して…
In[5]:= Norm[ 1 ]
Out[5]= √(2π) ← 関数 1 の大きさはこれだ，という感じ．
In[6]:= Norm[ x ]
Out[6]= √(2/3) π^(3/2) ← 関数 x の大きさはこれということ．だから，
In[7]:= Norm[ x/%6 ] ← 関数 x / |関数 x| の大きさを計算すると
Out[7]= 1 当然 1 になる．
■ 直交性
内積が ゼロ になる二つの関数は「直交している」という．
→ 関係性，という観点から見れば，なんとなく言いたいことがわかるだろう．
例えば，{1, x, x2} という 3つの関数を見てみると，
In[8]:= InnerProduct[1, x]
Out[8]= 0
In[9]:= InnerProduct[1, x^2]
Out[9]= 2π^3 / 3
In[10]:= InnerProduct[x, x^2]
Out[10]= 0
となる．
最初の二つ {1, x} は互いに直交しているが，x2 はそうでない．
そこで，直交してない x2 を少しいじって
{1, x, x2+ax+b}
という3つの関数が互いに直交するようにできるか? と考えると…
In[11]:= InnerProduct[1, x^2 + a x + b]
Out[11]= 2 b π + 2π^3/3 ← これをゼロにしたい．
In[12]:= InnerProduct[x, x^2 + a x + b]
Out[12]= 2 a π^3/3 ← これもゼロにしたい．
より，a = 0, b = - π2/3 とすればよいことがわかる．
つまり，
{1, x, x2 - π2/3} の3つの関数は互いに直交する．
□ レポート課題 1
関数が {f1, f2, f3, ... , fn} と n 個ある時に，
それらから全て互いに直交するような n 個の関数を作るにはどういう手順で計算すればよいか考えよ．
(ただし，それが可能だというのは前提とする)
■ 正規直交基底 … ノルムが 1 で互いに直交する関数の組で…
n 個の関数 {f1, f2, .... , fn} が互いに直交し，かつ，各々のノルムが全て 1 であるとき，
この関数の組は正規直交な組であるという．
→ この正規直交性は非常に便利なので，よく使われる．だから特別に単語がある，というわけだ．
例えば，上の {1, x, x2 - π2/3} の3つの関数から正規直交なものを作るとすると，直交性はもう確保されているので，ノルムだけ合わせればよい．
で，
In[13]:= a = {1, x, x^2 - Pi^2 /3}
In[14]:= Map[Norm, a]
Out[14]= {√(2π), √(2/3) π^(3/2), (2/3)√(2/5) π^(5/2)}
In[15]:= b = a / %14
Out[15]= {1/√(2π), √(3/2) x/π^(3/2), (3/2)√(5/2) (x^2 - Pi^2 /3) /π^(5/2)}
と計算することで，3 つの関数からなる正規直交な組
{1/√(2π), √(3/2) x/π3/2, (3/2)√(5/2)(x2 - π2 /3) /π^(5/2)}
が得られる．
実際，
In[16]:= Map[Norm, b]
Out[16]= {1, 1, 1}
より，正規性(= 各々のノルムが 1)が確認できる．
□ レポート課題 2
{1, x, x2, ... , x5} という 6 個の関数から，
正規直交な関数の組 {f1(x), f2(x), ..., f6(x)} を作れ．
■ 正規直交性の便利さ
さて，この正規直交な組がどのように便利か，を見てみよう．
まず，正規直交な関数の組 {f1(x), f2(x), ..., fn(x)} が用意されているとしよう．
そして，性質がよくわからない関数 g(x) があるとする．
そして，
g(x) が fk(x) の足し合わせで近似できると仮定してみる．
数式で書けば，
n
g(x) ≒ Σ Ck fk(x), ただし Ck (k=1,2,..n) は実数
k=1
と書けると仮定するということだ．
(ということは，正規直交な関数の個数が多ければ多いほど近似は良くなりそうだ)
この時，Ck は各々どのような値をもつか．
実は，Ck は {f1,.. fn} の正規直交性から，
Ck = (g, fk)
と簡単に計算できるのである．(確認せよ!)
よって上の式を書き直すと，
n
g(x) ≒ Σ (g, fk) fk(x) ← この式のシンプルさは驚異でさえある!
k=1
となる．
つまり，内積さえ計算できれば，未知の関数 g(x) が知っている関数 fk(x)
の足し合わせで近似できる!
→ このように関数 g(x) を既知の直交する関数の組 {fk(x),...,fk(x)}
で展開することを「広義の」Fourier 展開という．
例えば，上で求めた3つの関数からなる正規直交な組
{1/√(2π), √(3/2) x/π3/2, (3/2)√(5/2)(x2 - π2 /3) /π^(5/2)}
を用いて，cos(x) を近似してみよう．
In[17]:= Map[InnerProduct[Cos[x], #] &, b] ← 上で求めた正規直交な組と cos(x) の内積を計算
Out[17]= {0, 0, - 3√10/(π^(3/2))} ← C1, C2, C3 が求まった．
In[18]:= Apply[Plus, b * %17]
Out[18] = - (45/2) (x^2 - π^2/3)/ (π^4) ← これが cos(x) をそれなりに近似しているはず
In[19]:= Plot[{Cos[x], %18}, {x, -Pi, Pi}] ← どれくらい近似しているかグラフで見よう．
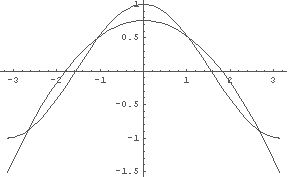← たった3つの関数からの近似ではこんなもの(^-^)
□ レポート課題 3
レポート課題 2 で求めた
正規直交な関数の組 {f1(x), f2(x), ..., f6(x)} を用いて，
sin(x) を近似(広義の Fourier 展開)してみよ．
さて，ここまでは正規直交な関数の組はどういうものが良いかということは考えてなかった．
そこで，歴史的に最初に提案されたものをチェックしてみよう．
それこそが Fourier(1768-1830) が提案した，「三角関数を正規直交な関数の組とする」
というものであり，これを用いての展開が「狭義の」Fourier 展開である．
これは，直交な関数の組として，
{1, sin(kx), cos(kx)} , k=1,2,..
を用いるというものである．
□ レポート課題 4
確かに {1, sin(kx), cos(kx)} , k=1,2,.. が直交している関数の組であることを
Mathematica で確認せよ．
(できたら数学的にも示せるとなお良い)
さて，この直交関数の組をさらに正規化しよう．
やり方は先のものと同様で，ノルムを計算して，そのノルムで割ればよい．
In[20]:= Norm[1]
Out[20]= √(2π)
In[21]:= Norm[Sin[k x]]
Out[21]= √(π- sin(2kπ)/2k)
In[22]:= Simplify[%, Element[k, Integers]] ← k は整数だ，と教えてあげると…
Out[22]= √π
In[23]:= Norm[Cos[k x]]
Out[23]= √(π+ sin(2kπ)/2k)
In[24]:= Simplify[%, Element[k, Integers]] ← k は整数だ，と教えてあげると…
Out[24]= √π
となるので，正規直交な関数の組は
{1/√(2π), sin(kx)/√π, cos(kx)/√π} , k=1,2,..
となることがわかる．
← 要するに，これを用いた展開が「狭義の」Fourier 展開である．
ただし，上の計算の途中で
● (決められた集合に)含まれると主張 … Element[式，集合(or クラス)] or 式 ∈ 集合
集合としては，Integers(整数)，Primes(素数)，Reals(実数)，
Complexes(複素数)… などがある．詳しくはマニュアルを見よ．
→ Simplify の仮定を表したりするのに使われる．
を用いている．
さて，ここまで来たのだから，(狭義の) Fourier 展開を楽しんでみよう．
まず，便宜のために
B0(x) = 1/√(2π)
B1(k,x) = sin(kx)/√π
B2(k,x) = cos(kx)/√π
と書くとしよう．すると，(狭義の) Fourier 展開は適当な n に対して
n n
g(x) ≒ (g, B0)B0 + Σ (g(x), B1(k,x)) B1(k,x) + Σ (g(x), B2(k,x)) B2(k,x)
k=1 k=1
となる(n が大きいほど近似度が良い)．
では，g(x) = x として，(狭義の) Fourier 展開を行ってみよう．
In[25]:= B0[x_] := 1/(2 Pi)^(1/2)
In[26]:= B1[k_, x_] := Sin[k x]/(Pi^(1/2))
In[27]:= B2[k_, x_] := Cos[k x]/(Pi^(1/2))
In[28]:= InnerProduct[g[x], B0[x]]
Out[28]= 0 ← (g,B0) はゼロになる．
In[29]:= Table[InnerProduct[g[x], B1[k, x]], {k, 1, 10}] ← (g,B1(k,・)) を k= 1..10 で求めている
Out[29]= …略…
In[30]:= Table[B1[k, x], {k, 1, 10}] ← そこで，B1(k,x) も列挙して，
Out[30]= …略…
In[31]:= Apply[Plus, %29 * %30] ← Σ(g, B1(k,・))*B1(k,x) を計算．
Out[31]= 2 Sin[x] - Sin[2 x] + 2/3 Sin[3 x] - 1/2 Sin[4 x] +
2/5 Sin[5 x] - 1/3 Sin[6 x] + 2/7 Sin[7 x] - 1/4 Sin[8 x] +
2/9 Sin[9 x] - 1/5 Sin[10 x]
In[32]:= Table[InnerProduct[g[x], B2[k, x]], {k, 1, 10}] ← (g,B2(k,・)) を k= 1..10 で求めている
Out[32]= {0,0,0,0,0,0,0,0,0,0} ← これは全部ゼロなので以下無視してよい．
つまり，Out[31] が g(x) の Fourier 展開になっているということだ．
In[33]:= Plot[{x, %31}, {x, -Pi, Pi}] ← どれくらい近似しているかグラフで見よう．
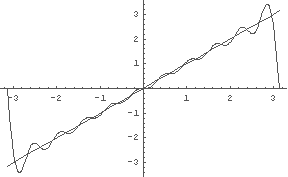← おお? 三角関数で y=x が近似できている.
そこで，この Fourier 展開を行ってしまう関数をプログラムしてみると，
In[34]:= FT[g_, n_] := Module[{t0, t1, t2, c1, c2, f1, f2},
t0 = InnerProduct[g, B0[x]] * B0[x];
c1 = Table[InnerProduct[g, B1[k, x]], {k, 1, n}];
f1 = Table[B1[k, x], {k, 1, n}];
t1 = Apply[Plus, c1 * f1];
c2 = Table[InnerProduct[g, B2[k, x]], {k, 1, n}];
f2 = Table[B2[k, x], {k, 1, n}];
t2 = Apply[Plus, c2 * f2];
Return[ t0 + t1 + t2]
]
← 関数 g を k=1,2,... n まで Fourier 展開する．
In[35]:= FT[x^2, 10] ← x2 を k=1,2,... 10 まで Fourier 展開してみると
Out[35]= …略…
In[36]:= Plot[{x^2, %35}, {x, -Pi, Pi}, PlotStyle -> {Hue[0], Hue[0.6]}]
← どれくらい近似できているか(色付きで)グラフを見ると，
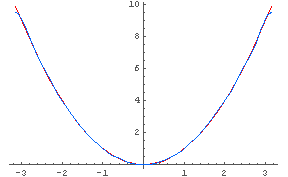← もうほとんど区別がつきにくくなっている．
□ レポート課題 5
g(x) = π-x (x ≧ 0 の場合), -x (x < 0 の場合)
という関数を(狭義の) Fourier 展開せよ．
また，どれくらい近似できているかグラフを示せ．
さて，ちょっとひねくれてみよう(^-^)．
上の(狭義の) Fourier 展開で求めたものは x ∈ [-π , π]
を想定していたのだが，その範囲の外ではどうなっているのだろうか?
In[37]:= Plot[{x^2, %35}, {x, -5 Pi, 5 Pi}, PlotStyle -> {Hue[0], Hue[0.6]}]
← 上のグラフの範囲を横に広げてみると…
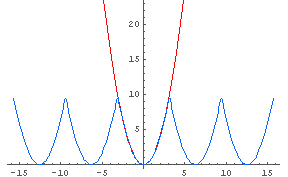← これは一体何が起こっているのだろう?
□ レポート課題 6
x ∈ [-π, π] の範囲の外では(狭義の) Fourier 展開はどうなるのか，
数学的に説明せよ．
>> 目次