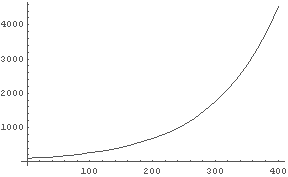
 ← かなりすごいことになっている
← かなりすごいことになっている
数学に限らず,なにか量の関係を調べるときには図やグラフ,
絵などにしてみるとよく理解できたり,新しい発見があったりする.
そこで,Mathematica を用いて簡単な図を作る方法に慣れ親しみながら,
図を操作したり図から何かを読み取ったりする力を養う.
● 関数の 2次元グラフを描く … Plot[関数, 変数の範囲]
→ 複数のグラフを同時にに描くには, Plot[{関数1, 関数2, ... }, 変数の範囲] とする.
10日借りると 1割の利息が複利でつく借金をしたとして,
x 日後に借金はいくらになっているか,関数を作ってグラフ化してみよう.
In[1]:= Pay[x_, gankin_] := gankin * (1.1^(x/10)) ← 元金を gankin としての x 日後の借金総額
In[2]:= Table[{n, Pay[n, 100]}, {n, 0, 100, 10}] // TableForm
Out[2]//TableForm= ← 100(万円)借りたとして借金がどうなるか10日毎に100日までの様子の確認.
0 100
10 110.
20 121.
30 133.1
40 146.41
50 161.051
60 177.156
70 194.872
80 214.359
90 235.795
100 259.374
In[3]:= Plot[Pay[x,100], {x,0,400}] ← 100(万円)借りたとして400日までの様子をグラフ化.
 ← かなりすごいことになっている
← かなりすごいことになっている
Out[3]= - Graphics -
例えば 3000(万円)になるのはいつか知りたい,という時は, とりあえず 3000(万円)のところに線を引いてみる. これは,y = 3000 という関数のグラフを同時に描くことだから,
In[4]:= Plot[{Pay[x, 100], 3000}, {x, 0, 400}] ← 2つのグラフを同時に描いている.
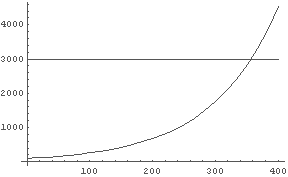
Out[4]= - Graphics -
とする.
そして,
● 2次元グラフのおよその値を知る
… グラフを選択後,Ctrlキーを押しながらカーソルを目的の場所へ
→ ノートブックの左下にカーソルの位置での座標が表示されるのでそれを読めばよい.
→ システムや Mathematica のバージョンによっては,Alt キー,
もしくは Altキー+Enterキー がその役割になる.
→ 教育計算機システムでは Alt キーがその役割.
という機能を使って,上のグラフ中の「交点」あたりの座標を読むと,およそ
355 日前後の時に 3000(万円)になるという目星が付く.
→ 複雑な問題の場合,正確な解を求める前に予備的な手段でこのように解の
「予測値」を得ておくのが良い.
そこで,x = 355 の周辺だけを方眼つきでグラフにしてみると(分かりやすいように色もつけて),
→ ● 図に方眼線を入れる … オプション GridLines
→ ● 図をカラーで … オプション PlotStyle
→
色の指定の際,Mathematica では Hue[a] (色相)を使うとパラメータが一つで済むので楽である.
0 ≦a≦1 で,色は 赤→黄色→緑→水色→青→紫(→赤へ戻る)となる.
もちろん,色(光)の三原色に基づく RGB(RedGreenBlue) 法で RGBColor[a,b,c] という指定方法も有効である.
を用いて…
In[5]:= Plot[{Pay[x, 100], 3000}, {x, 353, 358}, GridLines -> Automatic, PlotStyle -> {Hue[0], Hue[0.5]}]
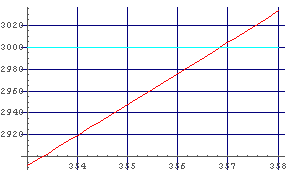
Out[5]= - Graphics -
357日目で 3000(万円)を越えることがわかるので,
さきほどつけた目星はなかなか良かったこともわかる.
では,次のような問題はどうだろう.
ある業者から100万円を借りる時に利息について次のような二通りの方法が選べるとしよう.
最初のうちは明らかに方法 1 の利息が安いが,いつまでもそうだろうか.
詳細に調べてみたらどうなるか.
→ 授業中の課題
われわれは時折,音の大きさが周期的に変化する(= 周期が秒単位という長めの)「うなり」を聞くことがある.
あの正体はいったい何だろうか.
音というのは空気圧の非常にすばやい変化(振動)を耳でとらえたものであるから,
振動する関数で様子を見よう.
それには,三角関数(sin, cos)がもっとも手っ取り早いので,そのうちの
sin 関数を用いてみる.
耳が聞くのは,空気圧が時間で変化する様子なので,わかりやすいように
ここしばらくは変数として時間変数 t を使う.
In[1]:= Plot[Sin[t], {t, 0, 10}] In[2]:= Plot[Sin[t], {t, 0, 100}]
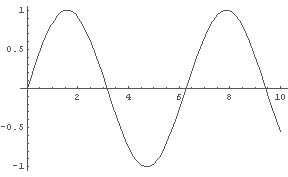
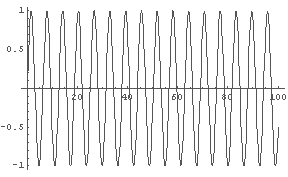
これはもっとも単純な振動する波である.
Sin[t] を Cos[t] や Sin[2*t] などに変えても絵的には変わらない.
これを音として聞くと,もっとも単純な機械的な音として聞こえる(純音).
ちなみに人間は,振動数(一秒に何回振動するか)が大きい ⇔ 音が高い と認識する.
より詳しく言うと,振動数が 2倍 ⇔ オクターブが1上がる という認識.
音の大きさは,振動の振幅(グラフで言えば上下の幅)に相当する.
In[1]:= Plot[Sin[t*2*Pi], {t, 0, 1}] In[2]:= Plot[Sin[5*t*2*Pi], {t, 0, 1}]
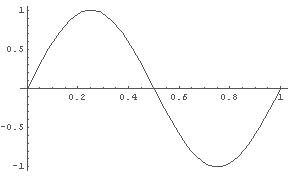
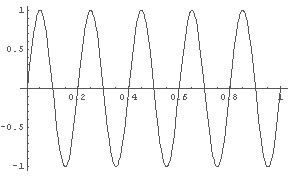
振動数 1(Hz) の波形と,振動数 5(Hz) の sin 波形
→ Sin[ ] 中の t に 2πがかかっているのは,数学では通常,ラジアン(という無次元単位)を使うからである.
よく知らない人は,「角度でいう 360°= 2π」だと思えばよい.
実は,グラフの波形をそのまま音として出力することが(機械によっては)できる.
● 関数を音として出力 … Play[関数,変数の範囲]
→ Plot と使い方はそっくりである.
→ 実際に音が出るかどうかは OS やシステムのハード構成などによって様々.
教育計算機システムの場合,(小さいが)きちんと音が出る.
ただし,通常は背面のイヤホン端子にケーブルが刺さっているため,
それを抜かないとスピーカから音が出ないので注意.
ヘッドホンを持参して用いるとはっきりと音が聞き取れて良いだろう.
ちなみに,Mathematica から音が出ないシステムの場合は,次の Export と Run を組み合わせる.
例えば上の sin 波形の音を聞くには
In[1]:= Play[Sin[3000*x], {x,0,10}]
などとすれば良い.
Sin[... x] の x の前にある程度大きな数字を入れておかないと,
周波数の関係で人間に聞き取れないことに注意.
● データをファイルに出力 … Export["ファイル名.拡張子", 式]
→ 式を評価したデータをファイルへ出力し,拡張子に対応する形式に変換する.
→ 対応する形式は非常に多いので,マニュアルを見るべし.
例えば 10秒分の 440Hz (「ラ」の高さ)の sin波形を音のファイル(wave形式)として
sound.wav という名前で出力したいという場合は,
In[1]:= Export["sound.wav", Play[Sin[440*t*2*Pi], {t,0,10}] ]
とする.
● Mathematica 外部のコマンドを実行する … Run["文字列1","文字列2",...]
or !コマンド
→ Run は,入力された文字列をスペースで区切ってつなげ,OS に渡す.
→ ! はそれ以降に入力された文字列を OS に渡す.
例えば unix 系の OS で sound.wav という名前の音声ファイルを再生したい時は,
In[1]:= Run["/usr/bin/playwave","sound.wav"]
などとする.
ただし,音声を再生するためのコマンド(この場合は playwave )が様々なので,
いろいろ調べる必要がある.
(また,! はいろいろな事情で使いにくいのであまり勧めない)
さて,実はあとでやる(予定の)フーリエ展開に関する理論からあらゆる波形は sin
と cos を適当に足し合わせたものだということがわかっているので,
まずは,一番シンプルな Sin[t] にいろいろな sin関数を足して変化を見る.
Sin[t] を基本として,足してみる sin 関数の振動数を,まずは少しずつ大きくして離してみると…
In[1]:= Plot[Sin[t]+Sin[2*t], {t, 0, 20}] In[2]:= Plot[Sin[t]+Sin[4*t], {t, 0, 20}]
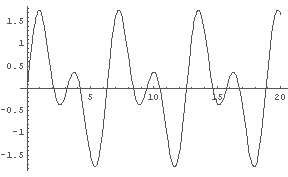
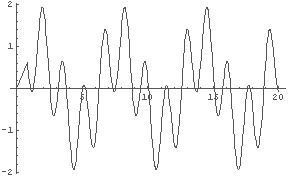
In[3]:= Plot[Sin[t]+Sin[6*t], {t, 0, 20}] In[4]:= Plot[Sin[t]+Sin[8*t], {t, 0, 20}]
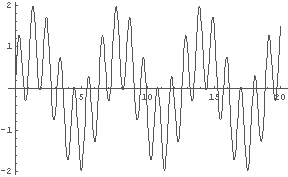
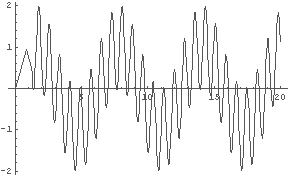
In[5]:= Plot[Sin[t]+Sin[10*t], {t, 0, 20}] In[6]:= Plot[Sin[t]+Sin[12*t], {t, 0, 20}]
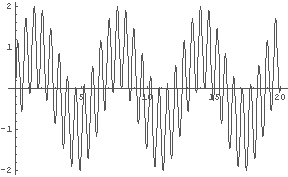
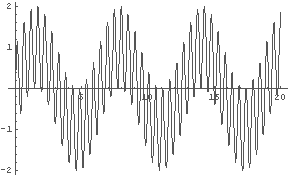
「うなり」になるには,周期が長くなる ⇔ 振動数が低くなる
という現象が発生しなければいけないのだが,上の図を見る限り,
sin(x) + sin(nx), n=1,2,3,.... というグラフにはそういうことはなさそうだ.
例えば,実際に音として上の図の波形を聞いてみると,単純に二つの音が鳴っている,と聞こえる.
では次に,足してみる sin 関数の振動数を,
少しずつ基本の Sin[t] に近づけていってみよう.
毎回 Plot… と入力するのも面倒だろうから,Table 命令と組み合わせて一度に出力してしまおう.
In[1]:= Table[ Plot[Sin[t]+Sin[(1+1/n)*t], {t, 0, 20}], {n,1,10}]
← sin(t) + sin((1.ほげ)t) を 10通り出力している.

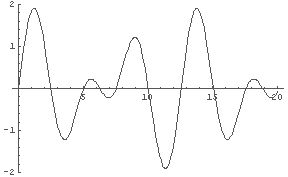
…略…
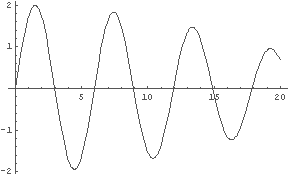
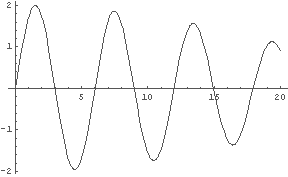
最後の Plot は sin(t)+sin(1.1t) であるが,少しずつ音が小さくなっていっているようだ. では,結局どうなるのか. 最後のグラフの範囲を広げてみよう.
In[1]:= Plot[Sin[t]+Sin[1.1*t], {t, 0, 200}]
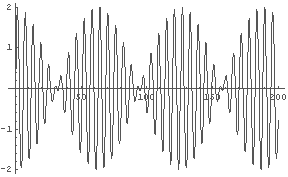
どうやら,全体が 200秒間に約 3回振動するという波形のようだ.
つまり,約 3/200 Hz という低い振動数だということであり,
これは立派な「うなり」である,といえる.
これから導ける仮説は,
■ 仮説1 振動数が近い sin 関数の和はうなりを生ずる
であるが,より一般的に次のように大胆に提案してみるとどうだろうか.
■ 仮説2 振動数が近い二つの波の和はうなりを生ずる
□ レポート課題 1
上の仮説1, 2 を Mathematica で確かめよ.
では,「うなり」の振動数は予測できるのだろうか?
結果が分かりやすいようにラジアン単位を意識して Plot を再びおこなってみよう.
In[1]:= k[t_] := 2*Pi* t ← 毎回 2*Pi*... と書くのは面倒なので
In[2]:= Table[ Plot[ Sin[k[t]]+Sin[(1+1/n)*k[t]], {t, 0, 50}], {n,10,20,2} ]
← 振動数の違いをちょっとずつ変えて出力
図は…略…
で,出力したグラフを見ながら「うなり」の振動数を目測でおよそ計ると,
次のような結果が得られる.
| (1+1/n)*2*Pi の n | 10 | 12 | 14 | 16 | 18 | 20 |
|---|---|---|---|---|---|---|
| 振動数(Hz) | 5回/50秒 = 1/10 | 約 4.2/50 | 約 3.5/50 | 約 3.2/50 | 約 2.7/50 | 約 2.5/50 |
そこで,これを (1+1/n) と比較してグラフにしてみよう(*2*Pi は面倒なのでほっておく).
→ ● 図の点をつなぐ(ListPlot専用) … オプション PlotJoined
→ ● 図の比率を正しく … オプション AspectRatio
というオプションを用いて…
In[1]:= a = {{1+1/10,1/10},{1+1/12,4.2/50},{1+1/14,3.5/50},
{1+1/16,3.2/50},{1+1/18,2.7/50},{1+1/20,2.5/50}}
In[2]:= ListPlot[a, PlotJoined -> True, AspectRatio -> Automatic]
Out[2]:=
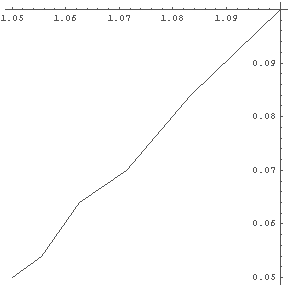
このグラフを良くみると次の二つの点に気づく.
これは結局,次のような仮説で言い換えられる.
■ 仮説3 振動数が近い sin 関数二つの和が生ずるうなりの振動数は,
sin 関数の振動数の「差」に等しい.
先ほどと同じように,より大胆には
■ 仮説4 振動数が近い波の和が生ずるうなりの振動数は,
それらの波の振動数の「差」に等しい.
□ レポート課題 2
上の仮説3,4 を Mathematica で確かめよ.
□ レポート課題 3
上の仮説1,2,3,4 を数学的に証明せよ.
→ 仮説2,4 の数学的証明は,フーリエ展開等を知らないと厳しいかもしれないので,知らない人は仮説2,4 の証明はあきらめても良い.