● 条件判断 … If [ 条件, 条件が真の時の式, 条件が偽の時の式 ]
● 表示 … Print[表示したいもの(カンマで区切って並べる)]
→ Print コマンドは「画面に出力はする」が,「関数の値にはならない」ことに注意.
そういう意味で,次の himan 関数はあまり良くない書き方になっている.
改善方法については,その次の Himando 関数のところで述べているのでそこを見よ.
例えば,BMI(Body Mass Index): 体重(kg) / (身長(m)^2) を見て太り過ぎかどうかの判定をする関数を考えてみよう.
(日本肥満学会では BMI が 25以上で肥満とする)
In[1]:= BMI[w_, h_] := w/(h^2) ← w:体重(kg), h:身長(m)
In[2]:= BMI[64, 1.68]
Out[2]= 22.6757
In[3]:= himan[x_] := If[ 25 <= x,
Print["BMI=",x, " is HIMAN"],
Print["BMI=",x, " is not himan"]
]
In[4]:= himan[BMI[64, 1.68]]
Out[4]= BMI=22.6757 is not himan
In[5]:= himan[BMI[75, 1.68]]
Out[5]= BMI=26.5731 is HIMAN
● 条件判断(多値) …
Which [ 評価式1, 式1, 評価式2, 式2, 評価式3, 式3,... ]
→ 評価式n を順に比較して,最初に True になる最初の n に対して 式n を実行
● 条件判断(多値) …
Switch [ 評価式, 評価1, 式1, 評価2, 式2, 評価3, 式3,... ]
→ 評価式と評価n を順に比較して,評価式が評価n にマッチする最初の n に対して 式n を実行
例えば,日本肥満学会では BMI に応じて
| BMI | <18.5 | 18.5≦ | 25≦ | 30≦ | 35≦ | 40≦ | |
|---|---|---|---|---|---|---|---|
| 分類 | 低体重 | 普通 | 肥満(1度) | 肥満(2度) | 肥満(3度) | 肥満(4度) |
と肥満症を分類しているので, この分類を行う関数を作ってみると次のようになる.
In[1]:= Himando[x_] := Which[
x < 18.5, Print["yase"],
x < 25, Print["futsuu"],
x < 30, Print["himan 1"],
x < 35, Print["himan 2"],
x < 40, Print["himan 3"],
True, Print["himan 4"] ← ここまで来たら必ず成り立つよう書かれている.
]
In[2]:= Himando[BMI[65,1.68]]
Out[2]= futsuu
In[3]:= Himando[BMI[120,1.68]]
Out[3]= himan 4
で,上の Himando 関数を他の関数から再利用したい,ということを考えると,
本当は Print コマンドは使わない方がよい.
なぜなら,Print 命令は「画面に出力はする」が,「関数 Himando の値にはならない」からである.
そう考えて改良すると,例えば次のように「関数 Himando の値として数字や文字列を返す」などとするのがよい.
In[4]:= Himando[x_] := Which[
x < 18.5, -1,
x < 25, 0,
x < 30, 1,
x < 35, 2,
x < 40, 3,
True, 4
]
In[5]:= Himando[BMI[65,1.68]]
Out[5]= 0 ← かえって分かりにくくなったような気が最初はするが…
こうすると,Himando を他の関数から例えば次のように簡単に利用できる. (Module については後述)
In[6]:= Advice[x_] := Module[{h, alist, r},
alist = {
"yasesugi desu. motto tabemasyo",
"futsuu desu. konomama ikimasyou",
"himando 1 desune. sukosi yasemasyou",
"himando 2 desu. kanari yabaidesu. yasero.",
"himando 3 da. yabai. yaseroyo.",
"himando 4. futorisugi. iikagen yasero."
};
h = Himando[x];
r = alist[[h+2]];
Return[r]
]
In[7]:= Advice[BMI[75, 1.68]]
Out[7]= himando 1 desune. sukosi yasemasyou
こうすることで,「肥満度の判定」と「アドバイス」を分離できたことが重要.
つまり,肥満度の判定の基準が多少変わっても Himando 関数を変更するだけでよく,
Advice 関数は変更しないで済む.
● 複雑な関数の定義 … Module
関数名[変数名_] := Module[局所変数のリスト,
式;
式; ← 必要なだけ
Return[式]
]
局所変数→ Module[ ] の [ ] の中でだけ有効な変数
Return→
関数の返り値. Return 文が無い場合,最後の式の値が返り値となる.
なるべくなら Return 文を使うのが良い.
というのも,最後の式の後ろに ;(セミコロン)をつけてしまうと
さらにそのあとに「空の式」があると Mathematica は解釈するので,
Return 文を使わない時 返り値がなくなる,と
いう陥りやすい落とし穴があるからである(^-^;).
(注) Mathematica では ; で区切られた式は「大きな一つの式」の扱いになる.
例えば,20% の消費税を課した場合の値段を計算する関数を作ると,次のような感じになる.
In[1]:= f[x_] := Module[{tax},
tax = 0.2;
Return[x * (1.0 + tax)]
]
in[2]:= f[120]
out[2]= 144
● Do[式, {i, min_i, max_i, step_i}]
→ step_i おきに i を min_i から max_i まで変えながら式を繰り返す.
● For[初期条件, ループ条件, 式2, 式1]
→ 初期条件を評価した後に,ループに入る.
各ループでは,ループ条件が満たされれば式1,式2 の順序で評価され,もう一度ループに入る.
ループ条件が満たされない場合,ループ終り.
→ Continue コマンドとの整合性のためにこのような仕様になっている.
ちょっと分かりにくいか.
ちなみに,Continue コマンドは使わない方が良い代表的なコマンドである.
よって紹介しない.
● While[条件, 式]
→ 条件が真ならば式を評価し,また条件をチェック,を繰り返す.
条件が偽になったら終り.
例えば,月の利息が 1% の借金をして,12ヶ月たつといくらになるか? を計算する関数をつくると,
In[1]:= Debt1[x_] := Module[{y},
y = x;
Do[y = y*1.01, {i, 1, 12}];
Return[y]
]
In[2]:= Debt2[x_] := Module[{y},
y = x;
For[i = 1, i <= 12, i++, y = y*1.01];
Return[y]
]
In[3]:= Debt3[x_] := Module[{y, i},
y = x;
i = 1;
While[i <= 12, y = y*1.01; i++]; ← y=..;i++ は大きな一つの式と見なされている
Return[y]
]
In[4]:= Debt1[100]
Out[4]= 112.683
In[5]:= Debt2[100]
Out[5]= 112.683
In[6]:= Debt3[100]
Out[6]= 112.683
→
i++ は(値を 1増やして元の値を返す)の省略形.
他にも
++i, i--, --i, i+=a, i-=a, i*=a, i/=a
などの省略した形式がある.→ Help で調べてみよ.
● 高階関数 … (Mathematica では)関数を引数にとる関数のこと
→ 数式処理ソフト特有のコマンド群である.使いこなせると上の繰り返し命令群を使うよりも便利なことが多い.
● リストの要素全てに関数を適用する … Map[関数,リスト]
→ Map で明示しなくても良いケースも多い.
In[1]:= a = {1,2,3,4}
In[2]:= Map[Sin, a]
Out[2]= {Sin[1],Sin[2],Sin[3],Sin[4]}
In[3]:= a // Sin
Out[3]= {Sin[1],Sin[2],Sin[3],Sin[4]}
In[4]:= Sin[a]
Out[4]= {Sin[1],Sin[2],Sin[3],Sin[4]}
In[5]:= % // N
Out[5]= {0.841471, 0.909297, 0.14112, -0.756802}
● 式の(レベル指定された)「頭部」を関数に置き換える … Apply[関数,式, レベル]
→ レベル指定を {1} として,リストの中身を書き換えるのに便利.
In[1]:= a = Table[Sin[n], {n,4}]
Out[1]:= {Sin[1], Sin[2], Sin[3] , Sin[4]}
In[2]:= Apply[Cos, a, {1}]
Out[2]= {Cos[1], Cos[2], Cos[3], Cos[4]}
In[3]:= Apply[Plus, a]
Out[3]= Sin[1]+Sin[2]+Sin[3]+Sin[4]
← レベル指定しないと,{0},すなわち最初の頭部と見なされる.
a は正確には List[Sin[1],Sin[2],Sin[3],Sin[4]] のことであるので,
これは Plus[Sin[1],Sin[2],Sin[3],Sin[4]] = ... と置き換えられる.
● 条件にあう要素をリストから取り出す … Select[リスト,条件関数]
→ 条件関数をリストの要素に適用して,True となるものだけを取り出す.
In[1]:= a = {1.0, -3, 5, 4, 3.5, -1.2}
In[2]:= Select[a, Positive]
Out[2]= {1.,5,4,3.5}
● 関数を引数に繰り返して適用 … Nest[関数,引数, 適用回数]
→ 例えば,Nest[f, x, 5] は f[f[f[f[f[x]]]]] を意味する.
月の利息が 3% の預金をするとして,100万円を預けると 2年後には複利で幾らになるか…
In[1]:= Debt[x_] := x * 1.03
In[2]:= Nest[Debt, 100, 24]
Out[2]= 203.279
● 関数を引数に繰り返して適用 … Fold[関数,引数, リスト]
→ Nest に似ているが,関数の第二引数がリストの要素になる.
→ 例えば,Fold[f, x, {2,1,5}] は f[f[f[x, 2], 1], 5] を意味する.
例えば,((1.32)0.7)1.2 を計算するには…
In[1]:= Fold[Power, 1.3, {2, 0.7, 1.2}]
Out[1]= 1.55391
自然数 n に対して,次のような関数 f を考える.
n/2 : n が偶数の場合
f(n) =
3n+1 : n が奇数の場合
例えば,f(1) = 4, f(2) = 1, f(3) = 10, f(4) = 2, .... となる.
● 偶数かどうかの判定 … EvenQ[数]
も用いて,上の関数 f は次のように Mathematica では定義できる.
In[1]:= f[n_] := If[EvenQ[n], n/2, 3*n+1]
In[2]:= Table[{n, f[n]}, {n, 1, 10}] // TableForm
Out[2]//TableForm=
1 4
2 1
3 10
4 2
5 16
6 3
7 22
8 4
9 28
10 5
さて,この f をある自然数 n に対して繰り返して適用するとどうなるか?
(計算量の無駄は覚悟して) Nest 命令を使ってみると,
In[3]:= Table[Nest[f, 1, m], {m, 20}] ← 1 に対して f を繰り返し使ってみる
Out[3]= {4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2}
In[4]:= Table[Nest[f, 2, m], {m, 20}] ← 2 に対して f を繰り返し使ってみる
Out[4]= {1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4}
In[5]:= Table[Nest[f, 3, m], {m, 20}] ← 3 に対して f を繰り返し使ってみる
Out[5]= {10, 5, 16, 8, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4, 2, 1, 4}
となる.めんどうなので,さらに n=10 まで Mathematica にやらせてみると,
In[6]:= Table[Nest[f, n, m], {n, 10}, {m, 20}] // TableForm
Out[6]//TableForm=
4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 2
1 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4
10 5 16 8 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4
2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1
16 8 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1
3 10 5 16 8 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1
22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1 4 2 1 4
4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 2
28 14 7 22 11 34 17 52 26 13 40 20 10 5 16 8 4 2 1 4
5 16 8 4 2 1 4 2 1 4 2 1 4 2 1 4 2 1 4 2
となり,どうも次のような仮説が成り立ちそうなのが素人目にも見て取れる.
■ 角谷(Kakutani)の予想
任意の自然数 n に対して関数 f を繰り返し適用するといつか必ず 1 になる
(その後は 1→4→2→1→4→... と繰り返す).
□ レポート課題 1
上の予想を Nest 命令を使わないで n=100 程度まで Mathematica で確認してみよ
さて,角谷の予想が正しいとすると f を何回繰り返せば 1 になるのかを次に考えてみよう.
In[7]:= KL[n_] := Module[{a, len},
a = n;
len = 1;
While[a =!= 1, a = f[a]; ++len]; ← =!= は ≠ の意味.
Return[len]
]
とすれば,自然数 n に対しては KL[n] 回 f を適用すれば 1 になることがわかる.
In[8]:= KL[1]
Out[8]= 1
In[9]:= KL[3]
Out[9]= 8
In[10]:= KL[5]
Out[10]= 6
さて,n と KL[n] には何か関係はないだろうか.
大量に計算して,
→
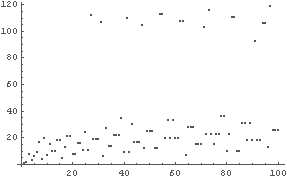
● 図の全ての範囲で隠さずに表示する … オプション PlotRange
を忘れずに使ってグラフで見てみよう.
In[11]:= a = Table[{n, KL[n]}, {n, 1, 100}]
Out[11]= …略…
In[12]:= ListPlot[a, PlotRange -> All] ← こうしないと Mathematica が気を効かせ(過ぎ)て,
上の部分をグラフ表示しない.

Out[12]= - Graphics -
□ レポート課題 2
n と KL[n] の間に何か関係がないか仮説をたて,確認してみよ.
□ レポート課題 3 (Mathematica 問題)
次の問題を Mathematica で解いてみよ.
10日で1割 という利子(複利)で 100万円の借金をした.
何日間借りたままでいると,借金が 1000万円に膨らむか.