● 式の比較 … <, <=, >, >=, ==, !=, ===, =!=
→ =(イコール) 一つで等価性判定にならない(代入になる)ことに注意
→ ===, =!= は各々 ==, != の「厳密バージョン」.
左右の式そのものを厳密に比較することになる.
普段は使わなくてよいだろう.
In[1]:= 3 <= 5
Out[1]= True
In[2]:= 3 >= 5
Out[2]= False
In[3]:= 3 == 5 ← 3 と 5 は等しいか? という式
Out[3]= False
In[4]:= 3 != 5 ← 3 と 5 は違うか? という式
Out[4]= True ← 確かに違うので True と答えが返ってくる.
In[5]:= 3 === 3.0 ← 3 と 3.0 は等しい「式」か?
Out[5]= False ← 式としては等しくないので False になる.
In[6]:= 3 =!= 3.0 ← 3 と 3.0 は違う「式」か?
Out[6]= True ← 確かに違うので True と答えが返ってくる.
● 仮定の下に単純な形式を得る … Simplify[式,仮定]
→ 仮定は省略できる
→ (不)等式の最も単純な形式は「正しいか否か」であるので,(不)等式の正否の判定にも使える
In[1]:= Simplify[Sqrt[x^2], x<0]
Out[1]= -x
In[2]:= Simplify[1/a < 1/b, 0 < b < a]
Out[2]= True
In[3]:= Simplify[1/a < 1/b, b < a]
Out[3]= 1/a < 1/b
In[4]:= Simplify[3 == 5]
Out[4]= False
(注) 仮定の条件が足りないと判定できない ⇔ 条件不足がわかる ことに注意
● 簡単な関数の定義 … 関数名[変数名_] := 定義
→ 左辺の変数名のあとについている _ (アンダースコア) を忘れがちなので注意.
→ 関数や変数の定義を消去するには,Remove[関数名(or 変数名)].
→ Clear も Remove に似た働きをするが,
完全に消去しないのでわかりにくい挙動が発生しうる.
In[1]:= f[x_] := Sin[x]
In[2]:= f[Pi/2]
Out[2]= 1
● パターンマッチング … _, __, ___
→ _ : 一つの式,__ :一つ以上並んだ式,___ :ゼロ個以上並んだ式
にそれぞれマッチする
→ パターンには「ラベル」をつけられる.簡単な関数の定義で用いた x_ はその例.
In[1]:= repeat[{x__,y__,y__,z__}] := {y}
In[2]:= repeat[{0,1,1,1,3,5,1}]
Out[2]= {1}
In[3]:= repeat[{1,2,3,4,5,3,4,5,6}]
Out[3]= {3,4,5}
● 実数の リスト 化 … RealDigits[数]
→ 実数の各桁の数字をリストの要素とし,
どこに小数点があったかわかるように,小数点以上の桁数とともに返
す.
→ 数が有理数の場合,
循環してない部分を a1, a2, …
無限循環反復部分を b1, b2, …
とすると,{a1, a2, …,{b1, b2, …}}
を返す.
→ FromDigits は逆の働き.
In[1]:= RealDigits[13.582]
Out[1]= {{1, 3, 5, 8, 2, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0}, 2}
In[2]:= RealDigits[15/7]
Out[2]= {{2, {1, 4, 2, 8, 5, 7}}, 1}
● リスト の要素を取り出す … [[番号]] → [[-1]] とすると最後の要素が出てくる
In[1]:= circular[x_] := RealDigits[x][[1]][[-1]]
In[2]:= circular[1/6]
Out[2]= {6}
In[3]:= circular[1/7]
Out[3]= {1, 4, 2, 8, 5, 7}
In[4]:= circular[1/8]
Out[4]= 5
(注) 割り切れている( ⇔ 循環している部分が無い)場合とそうでない場合の違いに注意
● リスト の要素数 … Length[リスト]
In[1]:= circularNumber[x_] := Length[circular[x]]
In[2]:= circularNumber[1/7]
Out[2]= 6
In[3]:= Table[{n, circularNumber[1/n]}, {n, 20}] // TableForm
Out[3]//TableForm=
1 0
2 0
3 1
4 0
5 0
6 1
7 6
8 0
9 1
10 0
11 2
12 1
13 6
14 6
15 1
16 0
17 16
18 1
19 18
20 0
● 変数への代入 … 変数名 = 代入したいもの
● リスト をグラフで見る … ListPlot[{{x1,y1},{x2,y2},...}]
In[4]:= a = Table[{n, circularNumber[1/n]}, {n, 200}]
Out[4]= …略…
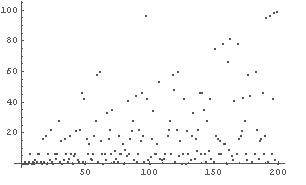
In[5]:= ListPlot[a]

Out[5]= - Graphics -
上のグラフをじっと見ると,
という事実に気づく.
上の表も一緒に見ながらこれを数学的に仮説にすると,次のように言い換えられる.
■ 仮説 1/n の周期は (n-1) 以下である
■ 仮説 n が素数ならば (n-1) の約数が 1/n の周期である
(素数でない場合は素因数分解すると… →考えてみよ)
● 素数 … Prime[n] → n番目の素数
In[6]:= Table[{Prime[n], circularNumber[1/Prime[n]]}, {n, 20}] // TableForm
Out[6]//TableForm=
2 0
3 1
5 0
7 6
11 2
13 6
17 16
19 18
23 22
29 28
31 15
37 3
41 5
43 21
47 46
53 13
59 58
61 60
67 33
71 35
● 余り … Mod[a,b] → a ÷ b の余り
In[1]:= Table[{Prime[n], circularNumber[1/Prime[n]],
Mod[Prime[n] - 1, circularNumber[1/Prime[n]]]}, {n, 20}] // TableForm
Out[1]//TableForm=
2 0 Mod[1, 0]
3 1 0
5 0 Mod[4, 0]
7 6 0
11 2 0
13 6 0
17 16 0
19 18 0
23 22 0
29 28 0
31 15 0
37 3 0
41 5 0
43 21 0
47 46 0
53 13 0
59 58 0
61 60 0
67 33 0
71 35 0
この事実は実は,次の定理を反映している
■ Fermat の(小)定理
a と p が互いに素で p が素数ならば a(p-1) - 1 は p で割り切れる
□ レポート課題 1
上の仮説(いくつかあるが)を Mathematica で確認してみよ
□ レポート課題 2
RealDigits コマンドを用いないで,同様の計算をおこなってみよ
→ ただし,次週に学習する「簡単なプログラミング」能力が必要かも